对于大、中河流一、二级评价，有时需要对河宽方向有更细致的认识，这时就需要采用二维模式。
1.持久性污染物扩散方程
持久性污染物一维扩散方程为：
假定污染物排入河流后在水深方向(z方向)上很快均匀混合，而x方向和y方向存在浓度梯度时，建立起二维扩散方程基本模型
式中 Edx——x坐标方向的弥散系数；
ux——x方向的流速分量；
Edy——y坐标方向的弥散系数；
uy——y方向的流速分量。
2.二维扩散方程在无限宽河流上的解析解
对于均匀河段，只考虑x方向的流速ux=u，认为uy为0，且整个过程是一个稳态的过程，则有：
在无限宽河流上，坐标原点设在污染物排放点，如图7-11 (a)所示，污染物浓度的分布呈高斯分布，则式(7-63)的解为：
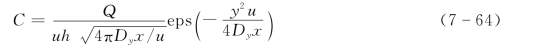(www.xing528.com)
式中 Q——连续点源的源强，g/s。
计算结果C的单位为g/m3。
3.二维扩散方程在有限宽河流上的解析解
自然界的河流都有河岸，河岸对污染物的扩散起阻挡及反射作用，增加了河水中的污染。多数排污口位于岸边的一侧。可以仅考虑本岸的反射，可将河流看作半无限宽河流。当设岸边排放源位于河流纵向坐标x=0处，如图7-11 (b)所示，岸边排放连续点的像源与原点源重合，下游任一点的浓度为：
对于需要考虑本岸与对岸反射的情况，如果河宽为B，如图7-11 (c)所示，只计河岸一次反射时的二维稳态河流岸边排放连续点源水质模型的解为：
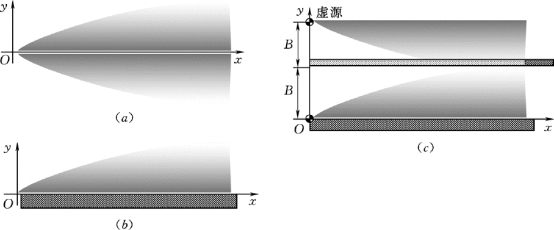
图7-11 均匀河段连续点源的三类排放模式
(a)无限大流场；(b)半无限大流场；(c)两岸反射
4.完成横向均匀混合的距离
根据横向污染物浓度的分布状况，若某断面上河对岸浓度达到同一断面最大浓度的5%，定义为污染物到达对岸。这一距离称为污染物到达对岸的纵向距离，用镜像法计算。本岸C(Lb，0)计算时不计对岸的反射项。污染物到达对岸C(Lb，B)，只需要考虑一次反射。使用式 (7-66)计算浓度，并按定义C(Lb，B)/C(Lb，0)=0.05解出的纵向距离Lb为：
虽然理论上讲，用镜像法计算时，如果纵向距离相当大，两岸反射会多次发生。然而，多数情况下，随着纵向距离的增加，点源的作用衰减得十分迅速。正态分布曲线趋于平坦，横向浓度分布趋于均匀。实际应用中，若断面上最大浓度与最小浓度之差不超过5%，则可以认为污染物已经达到了均匀混合。由排放点至完成横向均匀混合的断面的距离称为完全混合距离。由理论分析和实验确定的完全混合距离，按污染源在河流中心排放和污染源在河流岸边排放的不同情况，可将完全混合距离表示为：
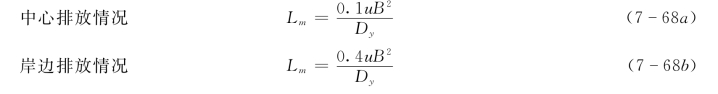
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
