污染物在水体中的迁移与转化过程

污染物在水中的物理迁移过程主要包括：污染物随水流的移流与扩散；受泥沙颗粒和底岸的吸附与解吸附作用而使污染物沉淀与再悬浮；底泥中污染物的输送等。

1.移流 （对流或平流）与扩散

一般情况下，排入河流的工业废水和城市生活污水中的污染物，主要呈溶解状态和胶体状态，它们形成微小的水团，随水流一起迁移和扩散混合。污水从排放口排入河流后，在推移、扩散的作用下，污染物随水流向下游迁移的同时，还不断地与周围的水体相互混合，得到稀释，使污染浓度降低，水质得到改善，因此，迁移和扩散是水体自净的重要形式。迁移扩散运动主要包括移流、分子扩散、紊动扩散和离散 (也称弥散)等形式。

(1)移流作用输移。河水移流运动是指以时均流速为代表的水体质点的迁移运动，习惯上也常称为对流运动或平流运动。对于某点污染物沿流向x的输移通量为：

式中 Fx——过水断面某点沿x方向的污染物输移通量，mg/ (m2·s)；

u——某点沿x方向的时均流速，m/s；

C——某点污染物的时均浓度，mg/m3。

则对于整个过水断面，污染物的输移率为：

式中 FA——断面A上的污染物输移率，mg/s；

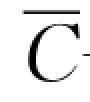——断面平均浓度，mg/m3；

Q——断面A的过水流量，m3/s。

(2)分子扩散作用输移。扩散作用是由于物理量在空间上存在梯度而使之在空间上趋于均化的物质迁移现象。水中污染物由于分子的无规则运动，从高浓度区向低浓度区的运动过程，称分子扩散。分子扩散过程服从费克 (Fick)第一定律，即单位时间内通过单位面积的溶解物质的质量与溶解物质浓度在该面积法线方向的梯度成正比，数学表达式为：

式中 Mmx——在x方向由于分子扩散作用污染物在单位时间内通过单位面积的质量，称为分子扩散通量，mg/(m2·s)；

C——某点的污染物浓度，mg/m3；

Em——分子扩散系数，m2/s；

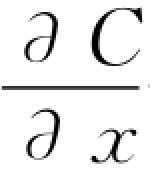——沿x方向的浓度梯度，它前面的负号表示污染物扩散方向与浓度梯度方向相反。

污染物在水中的分子扩散系数Em与污染物种类、温度、压力等因素有关，可通过实验测定，一般变化在10-9～10-8m2/s之间。

(3)紊动扩散作用输移。河流中水体的流动一般都是紊流，亦称湍流。紊流的基本特性是流动中所包含的各种物理量，如任一点的流速、压力、浓度、温度等都随时间而随机脉动。紊动扩散就是由紊流中涡漩的不规则运动(脉动)而引起的物质从高浓度区向低浓度区的迁移过程。紊动扩散通量，可采用类似分子扩散通量的费克定律表示为：

式中 Mtx——沿x方向污染物的紊动扩散通量，表示由于脉动作用使水中污染物在单位时间内通过单位面积的质量，mg/ (m2·s)；

Etx——x方向的紊动扩散系数，m2/s。

对于雷诺数Re=104左右的湍流流场，紊动扩散系数Etx可达3.36×10-4 m2/s，比上面提到的分子扩散系数Em大得多，可见河流中紊动扩散作用比分子扩散作用强得多。紊动扩散像分子扩散一样，可以发生在紊流流场中任一点的任一方向，但随着流场特性的不同，例如主要呈纵向流动的河流中，纵向、横向和垂向的紊动扩散系数是不同的，下面将进一步论述。

(4)离散(弥散)作用输移。上面关于污染物移流作用输送的分析，是以断面平均流速和平均污染浓度进行计算的。但在实际流场中，流速在断面上的分布往往很不均匀，岸边和底部流速较小，表面和中心流速较大，流速在横断面上具有一定的梯度，即所谓的剪切流。污染浓度也不均匀。在这种情况下，污染物随水流的输送，除前面已讲的移流输送、分子扩散输送、紊动扩散输送之外，还有由于断面流速和浓度分布不均匀而带来的离散作用的输送。

在河渠中，横断面上流速分布不均匀时，即在初始时刻 (t=0)污染物在断面A上均匀排入，如图7-1 (a)所示，但由于这些污染物将随断面上不同的质点以不同的流速向下游运移，经过一段时间 (t=t′)之后，污染物将在纵向发生显著的离散现象，如图7-1 (b)所示——多数以平均流速移到了断面B，有些流得快的则超前了，流得慢的则滞后了。

这种由于断面非均匀流速作用而引起的污染物离散现象也称为剪切流中的纵向离散或弥散。离散作用引起的污染物输送通量，也可用类似费克定律的形式描述，即

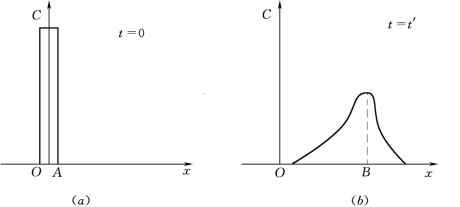
图7-1　河流中的纵向离散示意图

(a)t=0时浓度沿程分布；(b)t=t′时浓度沿程分布

式中 Mdx——污染物沿x方向的离散输送通量，表示由于水流的离散作用引起污染物在单位时间内通过单位面积的输送量，mg/ (m2·s)；

C——断面平均浓度，mg/m3；

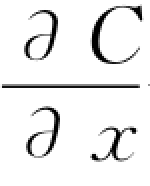——在x处断面浓度沿x方向的梯度；

Edx——纵向离散系数，m2/s，反映离散作用的大小。

在绝大多数的河流中，流场任意空间点的时均流速比脉动流速的绝对值至少要大出一个数量级，所以污染物的纵向离散作用远远大于单独的紊动扩散作用。通常Edx可达10～103m2/s的数量级，因此在天然河流中，一般情况下起主导作用的是纵向离散作用。

由于上述移流和扩散、离散作用的存在，废水排入河流后，一般会出现三种不同混合状态的区段，即竖向混合河段，横向混合河段和纵向混合河段。从排污口到下游污染物沿垂直方向达到混合均匀的地方所经历的区段，称竖向混合河段。竖向混合区段的长度与河流水深成正比，可为水深的几十倍或上百倍，但天然河流水深一般较浅，故竖向混合区段的长度相对是很短的。从竖向均匀混合到下游污染物在整个横断上均匀混合的区段，称横向混合河段。由于天然河流的宽度与水深相比一般有6倍以上，故横向混合区段的长度要比竖向混合区段长得多。横向混合河段之后的河段，称纵向混合河段。

费希尔(H.B.Fischer)按有边界限制的水流中污染源对流扩散公式，并以断面最小浓度与最大浓度之差在5%以内作为达到完全混合的标准，提出估算顺直河流中达到断面完全混合的距离的计算式如下。

对于在河流中心排污的情况：(www.xing528.com)

对于在岸边排污的情况：

式中 L——排污口至断面完全混合的距离，m；

u——河流断面平均流速，m/s；

B——水面宽度，m；

Ey——横向扩散系数，m2/s。

2.污染物的吸附与解吸附

当水中溶解的污染物或胶状物与悬浮于水中的泥沙等固相物质接触时，这些污染物或胶状物将被吸附在泥沙表面，并在适宜的条件下随泥沙一起沉入水底，使水的污染浓度降低，起到净化作用，这种作用称为吸附；与之相反，当水体条件 (如流速、浓度、p H值、温度等)改变时，被吸附的污染物也可能又溶于水中，使水体的污染浓度增加，这种作用称为解吸附。研究表明，吸附能力远远大于解吸附能力，因此，吸附——解吸附作用总的趋势是使水体污染浓度降低。

吸附过程是一种复杂的物理化学过程。如果吸附剂与被吸附物质之间因分子引力而引起吸附，称为物理吸附；如果二者间因化学作用，由化学键力而引起吸附，称为化学吸附。物理吸附和化学吸附往往相伴发生，共同产生吸附作用。目前水质计算中常用两种形式来描述这种作用：①弗劳德利希(Freundlich)吸附等温式；②海纳利 (Henery)吸附等温式。具体采用何种公式，可通过拟合实验资料确定。弗劳德利希吸附等温式可表示为：

式中 Se——吸附达到平衡时水中泥沙的吸附浓度，等于泥沙吸附的污染物总量除以泥沙总量，μg/g；

Ce——吸附平衡时水体的污染浓度，μg/L；

k、n——经验常数。k、n与水体温度、污染物性质、浓度等因素有关，可通过实验资料率定。如图7-2所示，湘江某断面水样在温度10℃下泥沙对汞(Hg)的吸附等温线，其k=36.0，n=1.84。

由7-8a式可进一步导出泥沙对水中污染物的吸附速率方程为：

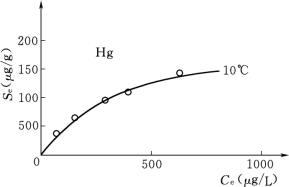
图7-2　湘江某断面汞的吸附等温线

式中 S——t时刻的泥沙吸附浓度，μg/g；

ζ——无量纲化的S值，数值上与S相等，但无量纲；

C——t时刻的水体污染浓度，μg/L；

W——水体的含沙量，g/L；

b——与活化能有关的指数；

k1，k2——吸附速率和解吸附速率系数，s-1。

通过对污水水样S、C、W 过程的监测，可分析求得k1，k2和b值。表7-1所示为湘江株洲河段的k1，k2和b值。

表7-1　湘江株洲河段的k1，k2和b值

由上述分析结果可见，对于不同的污染物，b比较稳定，k1比k2可相差几个数量级，对污染物的吸附计算k1起决定作用，因此应着重分析k1与其相关因素的关系，以便获得该实际条件下比较准确的k1值。

当取式(7-8a)中的n=1时，得到海纳利吸附等温式，即一阶动力学吸附方程：

并近似得到吸附速率方程为：

式中 Sm——泥沙的最大吸附浓度，与水体温度、p H值、污染浓度等因素有关，可近似地由式(7-9a)计算得出。

3.污染物的沉淀与再悬浮

污染物的沉淀与再悬浮，是影响水质的一个重要因素。比如，水中悬浮的泥沙，当含量过多时，将使水体浑浊，透光度减少，妨碍水生生物的光合作用和生长发育；当大量的泥沙淤积时，会使河床抬高，堵塞河道，引起洪水泛滥，因此，河流泥沙问题的研究，很早以来就受到高度重视，现在已经发展成为一支专门的学科——河流动力学或河流泥沙工程学。

研究水中污染物沉淀与再悬浮的计算原理与方法，对掌握水体污染的变化规律是十分重要。

在水环境数学模型中，关于污染物沉淀与再悬浮的计算，可采用两种途径进行。一种是按照河流动力学原理，先计算河段含沙量变化过程和冲淤过程，然后考虑泥沙对污染物的吸附—解吸附作用，进一步算出污染物的沉淀与再悬浮。这种方法考虑因素全面，计算精度较高。但需要资料多，计算工作量大，应用尚不广泛。另一种方法，是采用下面的公式进行估算，即

式中 C——水中污染物在t时刻的浓度；

Kc——沉淀与再悬浮系数，沉淀时取正号，表示水中污染物减少；再悬浮时取负号，表示该项作用使水体污染浓度增加。Kc与水流速度、泥沙组成、温度等因素有关，可通过相近的工程资料来选定。