宏观均匀性分值的优化方法

ISO/TS 18621-21：2020标准方法用一个宏观均匀性分值（Macro-Uniformity-Score）表征因一维周期性亮度波动的条纹、条带构成的二维非均匀性程度。方法的核心为：对输出的测试页面沿水平和垂直方向上均匀分割成数个子区，由众多子区的颜色得到一个最终的均值色差，即宏观均匀性分值（Macro-Uniformity-Score）。

标准要求样本的测试页采用A4幅面，采样区域最小宽度（最小高度）应为156mm，由平网填充区域构成，其数字文档宜以pdf格式存储及输出。测试页采样区域假定子区间距为6mm，可形成一个31×26的二维子区网格。典型的测试页图像如图4-14所示，两侧带有的标记可用于颜色的自动扫描测量。

标准同时指出，用于输出的每个单独测试图数字应在指定的色空间中，如单色K、RGB、CMYK或专色。使用的色值和颜色编码没有任何限制，但为了能够在设备、基材和墨水间使测试结果可比较，通常使用如下建议的颜色数值：

（a）C，65%；M，50%；Y，50%；K，50%。

图4-14　可用于自动扫描测量的带标记测试页

（b）C，40%；M，30%；Y，30%；K，30%。

（c）C，20%；M，15%；Y，15%；K，15%。

在不适合使用CMYK值的情况下，可使用如下CIELAB颜色值（M1、白衬底测量条件）：

（a）CIELAB = [32，-2，-2]。

（b）CIELAB = [52，0，-3]。

（c）CIELAB = [72，1，-4]。

测量仪器应符合ISO 13655标准，测量孔径（直径）不小于3mm，不大于6mm。测量用衬底应为白色，并符合ISO 13655：2017附录A条件。在打印输出的情况下，同时要考虑打印输出使用的再现意图。

对于31×26的二维子区网格情况，子区分布如图4-15所示。

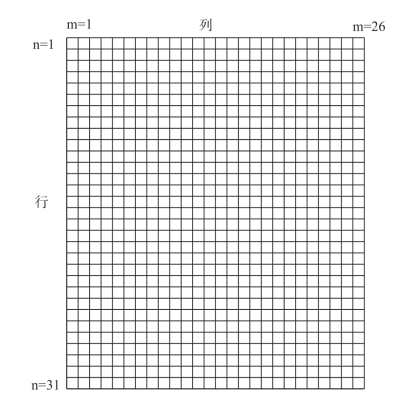
图4-15　测量子区分布

对输出的印刷图像样本，对照图4-15，宏观均匀性分值（Macro-Uniformity-Score）的测量过程如下：

（1）测量所有子区的CIELAB色度值，并按式（4-18）、式（4-19）分别求取行、列子区的平均色度。

如图4-15所示，在31×26二维子区（n=31、m=26，共806个）的情况下，若颜色测量子区外侧周长处于印刷区域内，则测量所有子区的CIELAB颜色值；否则，测量区域外侧周长一圈的所有子区（第1行、最后1行，第1列、最后1列）忽略不测，则测量并存储其余子区（为29×24，即n=29、m=24，共696个）的颜色值。(www.xing528.com)

（2）使用式（4-20）、式（4-21）计算每列相邻平均子区之间，以及每行相邻平均子区之间的CIEDE2000色差。对于n=29行和m=24列的A4版面样品，根据行计算将有28个色差，根据列计算将有23个色差。

（3）由式（4-22）、式（4-23）分别求行色差和列色差，进一步由式（4-24）计算总色差。

（4）由式（4-25）计算宏观均匀性分值（Macro-Uniformity-Score），式中的因子40和15为与心理物理数据拟合得到的最佳参数。

式（4-25）中的SMU即为宏观均匀性分值（Macro-Uniformity-Score）。也可缩写为MUS或MUS-score。

宏观均匀性分值没有测量单位，数值范围在0～100，根据四舍五入的原则取整数。

应用实践表明，式（4-25）所给出的SMU与静电成像打印及喷墨打印系统的条纹和条带的感知非均匀性有很好的相关性。

因其基本的颜色数据来源于不小于3mm直径圆形区域的平均色度，因此不难理解，该均匀性质量测度没有计量非均匀性的高频成分，如由于喷嘴缺陷造成的丝状颜色缺失等。

图4-16为宏观均匀性分值SMU随总色差ΔEt变化的曲线关系。可以看出，SMU随ΔEt的增大迅速降低，0.5的CIEDE2000色差 ΔEt就已使SMU降到了40，而到2.5的ΔEt总色差情况，SMU已近似为0。

图4-16　宏观均匀性分值随总色差的变化关系

如果将该测评方法应用到如图4-17所示两个K色较为极端的情况，可得到SMU及由水平和垂直方向色差各自对应的宏观均匀性分值结果如表4-3中SMU行数据所示。表中同时给出决定SMU结果的色差值，即公式（4-25）对应的色差。

图4-17　宏观均匀性

表4-3　图4-17样本的宏观均匀性特征值

表4-3数据给出了图4-17中（a）、（b）两个样本的宏观均匀性特征值，由公式（4-25）决定的总SMU值分别是0和12，对于0～100的数值表征范围，这两个数值无疑是极低和很低的，与该两个样品的视觉非均匀性相对应，可体会该指标的表现力。

表4-3中同时给出了构成总色差的水平和垂直两个方向色差形成的宏观均匀性测度值SMU，以及各自对应的色差值。不难看出，这两个样本均表现为沿水平方向变化形成的色差（对应视觉上的竖条纹）较沿竖直方向变化形成的色差（对应视觉上的横条纹）大得多，是其非均匀性的主要成因。尤其是图4-17中样本（b）的情况，沿垂直方向的绝对均匀（没有横条纹，SMU值为100），也没能使总体均匀性更好，仅12的总SMU值似乎体现了这一点，并与其视觉效果相当。