选择从动件的运动规律优化方案

在凸轮机构中，凸轮轮廓曲线决定了从动件的运动规律，常见的从动件运动规律有等速运动规律、等加速—等减速运动规律、余弦加速度运动规律和正弦加速度运动规律等。下面分别介绍。

1.多项式运动规律

1）一次多项式运动规律

从动件的速度为定值的运动规律称为等速运动规律（一次多项式运动规律）。设凸轮做匀速圆周运动，转动角速度为ω，推杆的行程为h，可表示为

等速运动过程中的边界条件为：在开始位置时，δ=0，s=0；在终点位置时，δ=δ0，s=h；则可得C0=0，C1=h/δ0，故此可知，从动件推程的运动方程为

从动件在回程运动时，位移则是从最高位置向最低位置变化，故此位移是逐渐减少的，因此回程的运动方程为

图3-4 所示为等速运动规律中从动件推程的运动线图；由图可知，从动件在开始和结束处的速度都是瞬时变化，理论上此时会产生无穷大的加速度a 和惯性力F，因此会使凸轮机构受到极大的冲击力，这种冲击称为刚性冲击。

图3-4　等速运动规律中从动件推程的运动线图

2）二次多项式运动规律

等加速—等减速运动规律（二次多项多运动规律）的表达式为

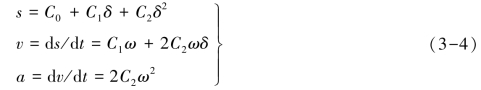
由式（3-4）可知，加速度为一定值，为保证凸轮运动的平稳性，在设计时通常采用加速段和减速段各占行程的一半；这时，从动件的加速段的边界条件为：

（1）在开始处：δ=0，s=0，v=0；

（2）在结束处：δ=δ0/2，s=h/2。

将开始和结束处的条件代入式（3-4）可得：C0=0，C1=0，C2=2h/δ20，因此可知从动件等加速推程的运动方程为

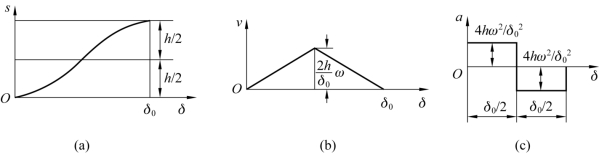
由式（3-5）可知，在此过程中，从动件的位移s 与凸轮的转角δ 的平方成正比，故其位移曲线为一段向上弯的抛物线，如图3-5 所示。

(www.xing528.com)

图3-5　等加速—等减速运动规律中从动件推程的运动线图

从动件的减速段的边界条件为：

（1）在开始处：δ=δ0/2，s=h/2；

（2）在结束处：δ=δ0，s=h，v=0。

将开始和结束处的条件代入式（3-4）可得：C0=h，C1=4h/δ，C2=-2h/δ20，因此可知从动件等减速推程的运动方程为

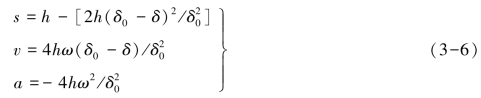
减速段中由于δ 的变化范围与加速段正好相反，所以从动件的位移是一段向下弯的抛物线。

2.三角函数运动规律1）余弦加速度运动规律余弦加速度运动规律又称简谐运动规律，其从动件推程的运动方程为

从动件回程的运动方程为

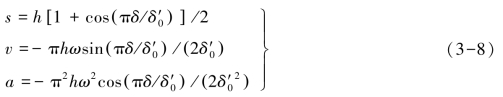
余弦加速度运动规律中从动件推程的运动线图如图3-6 所示。由图可知，在运动的始末位置时从动件的加速度有突变，故在开始和结束处有柔性冲击而无刚性冲击。

图3-6　余弦加速度运动规律中从动件推程的运动线图

2）正弦加速度运动规律

正弦加速度运动规律又称摆线运动规律，其从动件推程的运动方程为

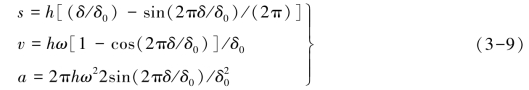
从动件回程的运动方程为

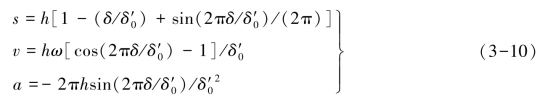
正弦加速度运动规律中从动件推程的运动线图如图3-7 所示。由图可知，其既无刚性冲击，又无柔性冲击。

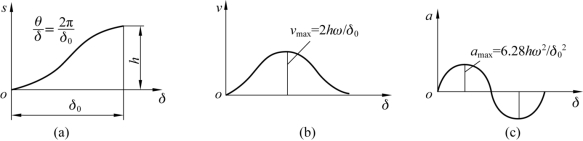
图3-7　正弦加速度运动规律中从动件推程的运动线图