【摘要】:图3-3 所示为一对心直动尖顶推杆盘形凸轮,图中凸轮的轮廓由曲线AB、BC、CD 和DA 组成。以图3-3 为例来介绍凸轮的基本参数。基圆——以凸轮的回转中心为圆心,凸轮轮廓曲线中最小尺寸为半径所作的圆为凸轮的基圆,r0称为基圆的半径。从动件在凸轮轮廓曲线的推动下,由最低位置上升至最高位置的运动过程称为推程,从动件上升的距离h 定义为升程,凸轮转过的角度δ0称为推程运动角。
图3-3 所示为一对心直动尖顶推杆盘形凸轮,图中凸轮的轮廓由曲线AB、BC、CD 和DA 组成。以图3-3 为例来介绍凸轮的基本参数。
(1)基圆——以凸轮的回转中心为圆心,凸轮轮廓曲线中最小尺寸为半径所作的圆为凸轮的基圆,r0称为基圆的半径。
(2)推程——图3-3 中从动件此时位于A 点,处于最低位置,当凸轮以角速度ω 逆时针转动时,凸轮从距离圆心最近的位置开始转动至最远的位置,此时凸轮运动到B 点,转过的角度为δ0,从动件从最低位置上升至最高位置。从动件在凸轮轮廓曲线的推动下,由最低位置上升至最高位置的运动过程称为推程,从动件上升的距离h 定义为升程,凸轮转过的角度δ0称为推程运动角。
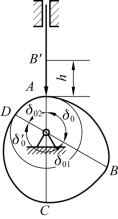
图3-3 对心直动推杆盘形凸轮(https://www.xing528.com)
(3)远休——凸轮继续以角速度ω 转动时,曲线BC 是以O 为圆心的一段圆弧,圆弧所对应的角度为δ01,凸轮转动过程中,从动件在最高位置保持不动,这一过程称为远休。
(4)回程——当凸轮继续转动后,凸轮与从动件的接触位置从距离凸轮回转中心最远的位置转到最近的位置,从动件由最高位置下降到最低位置,这一过程称为回程,凸轮在回程中转过的角度δ′0称为回程运动角。
(5)近休——曲线DA 是以O 点为圆心的一段圆弧,凸轮在转动过程中,从动件位置不发生变化,这一运动过程定义为近休,凸轮转过的位置角度δ02称为近休止运动角。
当凸轮不断地做回转运动,从动件不断地重复从最低位置到最高位置。所谓从动件的运动规律就是从动件的位移s、速度v 和加速度a 随凸轮转角δ 的变化规律。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




