计算自由度的几种情况需要注意

在计算自由度的过程中，判断机构是否具有确定的运动时，可能会出现以下几种特殊情况，需多加注意。

1.复合铰链

在机构中，有2 个或2 个以上的构件同时用转动副连接在1 个轴线上，这样的连接形式称为复合铰链。图1-7 为3 个构件用转动副连接在一起的运动简图，3 个构件共组成了2 个转动副。由此可知，若复合铰链是由K 个构件组成的，则连接处的转动副就有K-1个。在计算平面机构的自由度时，应注意机构中是否存在复合铰链，避免算错机构的自由度数目。

图1-7　复合铰链

2.局部自由度

某些机构中，某些构件产生的局部运动并不会影响其他构件的运动，这种局部运动的自由度称为局部自由度。如图1-8 所示，为减少凸轮和推杆之间的磨损，在两者之间加了一个滚子，该滚子绕自身轴线转动，它的存在并不会影响凸轮和推杆的运动，所以它仅有局部自由度。计算自由度数目时，应将局部自由度从自由度公式中减去。设局部自由度数目为F′，实际自由度数目则为

图1-8 中，实际自由度数目应为

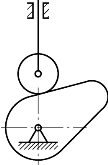
图1-8　凸轮机构

3.虚约束

在机构中，有些运动副引入的约束对机构的运动起到重复约束的作用，这类约束称为虚约束。在图1-9（a）所示的平行四边形机构中，原动件1 运动时，连杆2 做平移运动，连杆2 上的点的运动轨迹均为以半径等于DA 且圆心在直线CD 上的圆。如图1-9（b）所示，为保证运动连续性，机构中加了一个与原动件1 平行等长的构件5 和两个转动副E 和F，且AF=DE，但是对该机构的运动并没有产生任何影响。此时如果按照式（1-2）计算机构的自由度，则有(www.xing528.com)

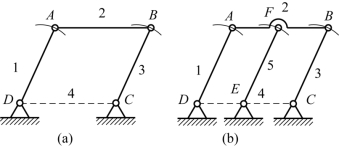
图1-9　平行四边形机构

在此机构中，如果按照上述情况计算，就认为增加1 个活动构件（增加3 个自由度）和2 个转动副（增加4 个约束）等于多引入了一个约束，其实这个约束对机构的运动只起重复约束的作用，是一个虚约束。在计算机构自由度时，应从机构的约束数目中减去虚约束的数目。设机构中虚约束的数目为P′，则机构的自由度计算公式为

因此，图1-9（b）中机构的自由度为

虚约束常常会出现在以下情况中。

（1）两构件组成多个导路平行的移动副。两构件组成2 个或2 个以上导路平行的移动副时，只有一个移动副具有独立限制作用，其余都属于虚约束。如图1-10 所示，直动从动件凸轮机构中的推杆与机架组成2 个移动副A1和A2，这2 个移动副都限制推杆只能沿竖直方向移动，所以其中只有1 个移动副起限制自由度的作用，另外1 个移动副是重复约束，属于虚约束。

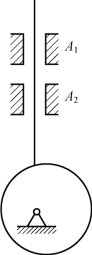
图1-10　两构件组成多个导路平行的移动副

（2）机构中对运动不起作用的对称部分。如图1-11 所示，行星轮系中有3 个行星轮与只有1 个行星轮从运动的角度来看效果完全相同，即行星轮系运动时，实际上只有1 个行星轮对轮系起到了约束作用，其他的2 个行星轮对轮系的运动没有独立的限制和约束作用。但为了改善受力情况和增加轮系刚度，轮系中采用了3 个行星轮。随着行星轮的增加，行星轮系机构中的运动副数量也随之增加，增加了2 个转动副和行星轮与中心齿轮构成的4 个高副。增加的行星轮和运动副对机构的运动不起作用，故属于虚约束。

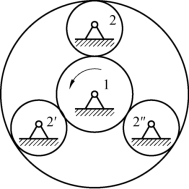
图1-11　行星轮系