在大多数情况下,水流充满整个水轮机流道,形成被固体边壁所包围及引导的内流运动。而大量的试验表明,对于存在固体壁面的充分发展的湍流流动,沿壁面法线的不同距离上可将流动划分为壁面区(或称内区、近壁区)和核心区(或称外区)。对核心区的流动,通常认为是完全湍流区。而在壁面区,流体运动受壁面流动条件的影响比较明显,壁面区又可分为3个子层:黏性底层、过渡层和对数律层。
黏性底层是一个紧贴固体壁面的极薄层,其中黏性力在动量、热量及质量交换中起主导作用,湍流切应力可以忽略,所以流动几乎是层流流动,平行于壁面的速度分量沿壁面法线方向为线性分布。过渡层处于黏性底层的外面,其中黏性力与湍流切应力的作用相当,流动状况比较复杂,很难用一个公式或定律来描述。由于过渡层极小,所以在工程计算中通常不明显划出,归入对数律层。对数律层处于最外层,其中黏性力的影响不明显,湍流切应力占主要地位,流动处于充分发展的湍流状态,流速分布接近对数律。
由于标准k-ε 模型是高雷诺数模型,针对充分发展的湍流才有效的,而对近壁区内的流动,雷诺数较低,湍流发展并不充分,湍流的脉动影响不如分子黏性的影响大,这样在这个区域内就不能使用标准k-ε 模型计算,必须采用特殊的处理方式。壁面函数法(wall functions)就是一种常用的处理方法,它是基于壁面湍流具有边界层特性的事实,从分析和实验中提出来的一组半经验的公式,其基本思想是:对于湍流核心区的流动使用k-ε 模型求解,而在壁面区不进行求解,直接使用半经验公式将壁面上的物理量与湍流核心区内的求解变量联系起来。这样,不需要对壁面区内的流动进行求解,就可直接得到与壁面相邻控制体积的节点变量值。(https://www.xing528.com)
划分网格时,不需要在壁面区加密,只需要把第一个内节点布置在对数律成立的区域内,即配置到湍流充分发展的区域,如图8-37所示。图中阴影部分是壁面函数公式有效的区域,在阴影以外的网格区域则是使用高Re数模型进行求解的区域。壁面函数公式就好像一个桥梁,将壁面值同相邻控制体积的节点变量值联系起来。壁面函数法针对各输运方程,分别给出联系壁面值与内节点值的公式。
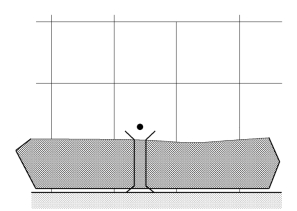
图8-37 壁面函数法网格示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




