水斗式水轮机的基本方程式解析

自喷嘴射出的射流以很大的绝对速度V0 射向运动着的转轮，如图2-14所示，V0 可由下式求得

图2-14　射流在水斗上的扩散

式中 KV——射流速度系数，一般为0.97～0.98；

H——自喷嘴中心算起的水轮机设计水头，m；

g——重力加速度，g=9.81m/s2。

在选定喷嘴数目Z0 以后，则通过Z0 个喷嘴的流量为

式中 d0——射流直径，m。

由于流速系数KV 的变化很小，可以认为在一定的针阀开度下，射流速度V0 的大小和方向均保持不变。当选取KV=0.97，则由已知的水轮机引用流量，便可得出射流直径d0 为

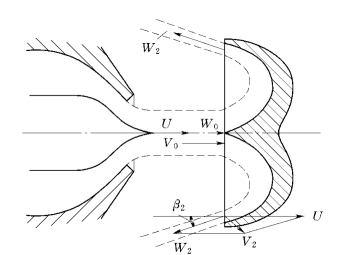
以速度V0、直径为d0 的射流冲击斗叶时，如图2-14所示，在A 点与斗叶的分水刃相垂直，水流在叶片处的进口速度V1 实际上就等于射流速度V0。此时可将斗叶的运动看成是平行于射流的直线运动，运动的速度即为圆周速度U1，则水流在斗叶进口处的相对速度W1=V0-U1=W0，W1 的方向与射流的方向一致。因此叶片进口处的速度三角形为一条直线，如图2-15所示。射流进入斗叶后，射流对斗叶的绕流运动近似看为平面运动，它沿着斗叶的工作面向相反的方向分流，在出口以相对速度W2 流出，W2 与U2 反方向之间的夹角即为斗叶的出水角，由此便可绘出水流在斗时出口处的速度三角形如图2-15所示，由于斗叶进口和出口距转轮中心的半径基本相同，可以认为U1=U2=U。

(www.xing528.com)

图2-15　水斗式水轮机的速度三角形

水斗式水轮机的转轮同样也改变着水流对主轴的动量矩，因此分析反击式水轮机工作原理时所导出的水轮机基本方程式（2-13）同样可适用于水斗式水轮机，将式中的V1 换成射流速度V0，可得

式中，U1=U2=U，进口角α1=0，在忽略了水流在水斗表面的摩擦损失之后，可认为水斗表面各点处的相对速度大小不变，则

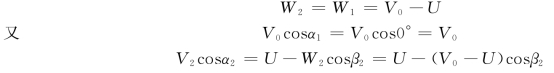
代入上式得

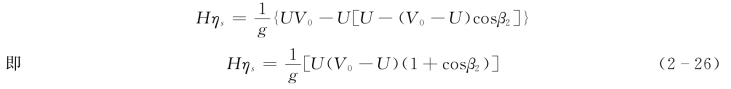
式（2-26）即为水斗式水轮机的基本方程式，它给出了水斗式水轮机将水流能量转换为旋转机械能的基本平衡关系。当水头为常数时，水轮机出力最大，也就是水力效率η0 最大的条件为：

（1）1+cosβ2 为最大，则β2=0，即水斗叶面的转角为180°。

（2）若β2 为某一固定角，UV0-U2为最大，则

这就是说，水斗叶片的出水角β2=0，射流在斗叶上进出口的转向为180°，并且转轮的圆周速度U 等于射流速度V0 的一半时，则水斗式水轮机的水力效率或出力最大。

但实际上，为了使水斗排出的水流不冲击下一个水斗的背面，叶片的出水角β2 并不等于零，一般采用β2=7°～13°；同时射流在斗叶曲面上的运动是扩散的，如图2-12所示，各点的圆周速度U 并不是均匀的，而且由于摩擦损失的影响，W2 也并不等于W1。因此，最大出力并不发生在U=0.5V0 时，根据实验，水斗式水轮机最有利的U/V0 的比值约为0.42～0.49。