互连驱动器模型的应用与优化

为了简化设计，片上互连的信号传输可以方便地分为两部分（见图8-9a）：从门（驱动器）的输入到门的输出，以及从互连的近端到远端（即接收器的输入）。这样信号时延被分解为门时延和互连时延。首先分别分析每一部分，然后将结果合并在一起计算总的时序。由于局部电路互连较短，因此局部电路的性能一般由门时延决定。然而，对于全局信号，互连时延至少与门时延一样重要，甚至有时由于互连过长，互连时延成为信号总时延的主要成分。为了减轻这个效应，全局互连驱动器的尺寸，包括逻辑门和插入的转发器都应该优化，使总的路径时延最小。另外，即使驱动器没有产生多余的噪声，其尺寸也强烈影响着串扰噪声的幅度：处于静态时的大驱动器提供了更好的直流到地连接，因此能够同时较好地抑制容性和感性耦合噪声。为此，获得适当的驱动器和门负载模型对有效分析和优化都非常重要。

一个开关驱动器可以建模为一个时变电压源^[29]或电流源^[30]，分别如图8-9b和图8-9e所示（注意接收器被简单地建模为在互连远端的负载电容器）。由一个斜坡电压源和一个线性电阻R_dr组成的Thevenin等效模型（见图8-9b）描述了门与互连负载之间的相互作用情况。例如，在典型的门时延分析中，使用模型降阶技术（如基于矩匹配的渐进波形估计^[31-33]），RC或RLC互连一般被近似为一个有效电容C_eff或单Π型电路（分别如图8-9c和图8-9d所示）。在这一近似下，计算R_drC_eff乘积可以很容易地求得门时延。另一方面，如果将开关门建模为单个电阻器，将很难准确地预测出门输出信号的实际压摆率，特别是如果输入的压摆率和负载电容的变化范围较大时更是如此。为了克服这一缺点，在实际的RC分析中，R_dr和C_eff值通过多次迭代匹配门输出波形上两点（如50%和90%）的方法拟合确定。例如，在表征单元库元件时，上述方法产生了一个作为负载电容和输入压摆率函数的R_dr值查找表。除了可用于预测门时延之外，Thevenin模型也提供了优化驱动器尺寸以使路径时延最小化的基础。在RC分析中采用上述做法的经验法则是下述条件成立^[34]：

门时延=线时延 （8.3.1）

(www.xing528.com)

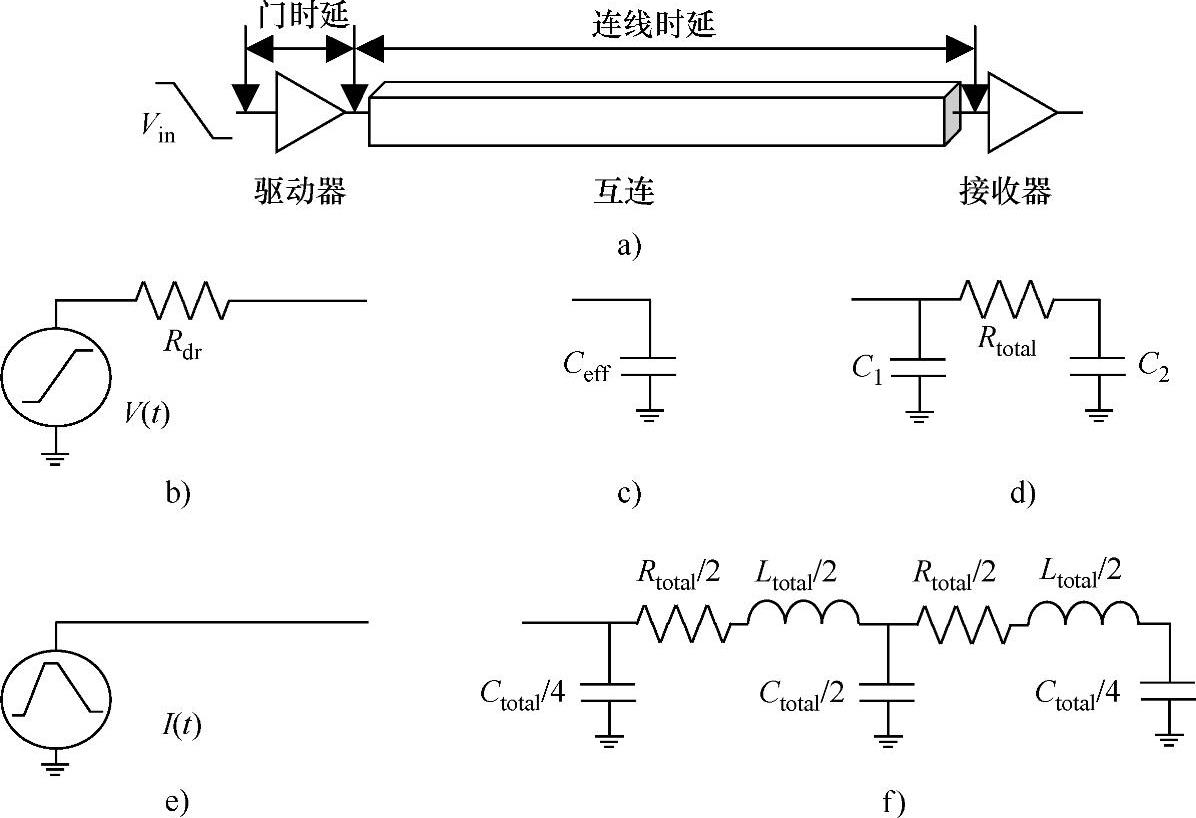
图8-9 计算门时延采用的各种驱动器[b）、e）]和互连负载[c）、d）、f）]模型

a）门时延和互连时延的定义 b）Thevenin模型 c）有效电容 d）单Π型模型 e）Norton模型 f）RLC互连的双Π型模型

除了用于常规的RC时序分析之外，Thevenin模型中的R_dr值不适用于预测串扰噪声，因为静态门总是处于线性工作条件下，而开关门则工作在线性区和饱和区。应该采用一个比R_dr值小的电阻对静态驱动器建模，进行信号完整性分析。而且单个线性电阻太简单，无法预测RLC分析中的全波特性；也无法获知电压过冲和信号振铃等高阶现象。采用时变电流源模型（见图8-9e）可以进行更精确的波形完整性分析，时变电流源模型实际是描述了整个开关范围内的晶体管行为^[30]。对RLC互连，使用更复杂的等效负载模型也是必要的。例如，为了反映互连近端和远端的波形反射^[30]，可以采用对称2-Π型RLC电路（见图8-9f）。（注意，在单Π型模型中，由于电阻的屏蔽效应，C₁和C₂不相等）