电感的频率相关效应分析及提取方法

在纳米领域，电感效应变得非常重要，特别是对全局互连。在进行RC提取时，仅需考虑互连本身和离它最近的相邻互连。电感耦合则与此不一样，它是长距离效应；又因为磁场很容易穿透金属表面，随着互连间距的增加衰减很慢。电感的基本定义为

式中，I为电流；B为I感应出的磁场；s为积分回路。如果s与I的路径相同，L就是自感；如果s路径与电流路径不同，式（8.2.11）定义的就是互感。这个定义表明电感具有沿着回路进行计算的特点，因此求解电感性特性必须考虑整个电流回路。然而，现代互连结构中（如图8-3a所示的驱动器-互连-负载电容），没有直流路径构成意义明确的回路。结果，返回电流一般要流经很长的范围，使得分析非常麻烦。因此，在进行提取分析时应考虑所有可能进入电流回路的所有相邻互连。

局部和回路电感 因为返回电流路径的不确定性，实际设计中很难计算回路电感（由式（8.2.11）定义）。为了解决这个困难，人们引入了局部电感的概念，其中假定感应电流从无穷远处返回，这样就回避了定义返回回路的问题。这种称为局部元件等效电路（Partial Element Equivalent Circuit，PEEC）法的电感计算技术非常适合设计自动化，因为它仅与互连的几何尺寸有关。基于PEEC法，一个由每个互连片段计算得到的L值所组成的通用局部电感矩阵如下所示：

然后，这个矩阵再与RC矩阵[式（8.2.7）]一起，借助于电路仿真器的计算，其结果就可以用于求解电流回路。这里，每个电感元件（即式（8.2.12）中的自感L_s或互感L_m）都可以使用场求解器，如FastHenry和Raphal，或解析解的形式计算。对矩形截面的互连，解析解首先由Rosa和Grover得到^[18]，且当1>>w、t和d时，简化为下面的关系式^[19]：

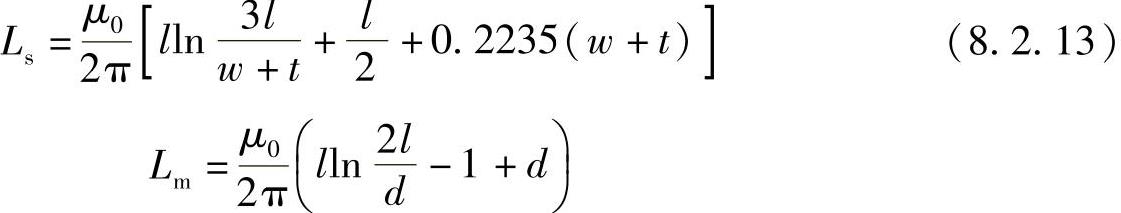
式中，μ₀为介质的导磁率；w、t和l分别为片段的宽度、厚度和长度；d为两条互连中心线之间的间距；L_m是两个长度相等互连的互感（在参考文献[19]中也给出了不相等互连L_m更普遍解的形式）。这些表达式说明了电感与片段长度之间是非线性关系。因此，与RC提取时其大小随互连线的长度缩放相比，L的计算必须考虑整个互连的长度。而且，式（8.2.13）中的对数函数意味着，同R和C与互连几何尺寸的相关度相比，L与互连几何尺寸的相关度更弱。注意，仅位于同一层且彼此平行的互连才对感性耦合有贡献；位于相邻层上的互连并不会影响耦合，由于它们的版图走向是正交的。

虽然采用PEEC法进行一般的电感提取时不需要预先给出电流返回回路的信息，但是，电感矩阵的非稀疏性（由长距感性耦合引起的）导致进行深入分析的巨大计算量^[20]。不像只保留短距耦合值就足够了的C矩阵，L矩阵不能通过截断加以简化；简单地舍去较远相邻互连间的L_m值会引起模型的不稳定^[21]。为了改善这种复杂矩阵的计算效率，已经做出了大量的努力。一个实例就是L矩阵截断法，它使用电源网格作为提取电纳矩阵的边界，而电纳矩阵是L矩阵的逆矩阵并且具有所需要的稀疏性^[22，23]。虽然迄今为止已经开发出了大量有效的计算技术，但是仍然没有一个与SPICE兼容且对片上互连结构而言既简单又通用的求解方法。一个近似的回路电感模型对评估电感的物理含义（式（8.2.11））是很有用的，特别是在设计开发的前期阶段。这个模型可以用查找表^[24]或解析模型的形式描述。后一种形式特别适合于与相邻互连之间通过电源和地线加以屏蔽的专用全局时钟结构^[25，26]。

频率相关的R（f）L（f） 以前只是在封装和微波设计时，由于互连线的尺寸太大，才考虑R和L的频率相关性。然而，当芯片的工作频率上升到GHz领域时，片上的互连也需要考虑这些效应。这是因为高频时电流穿通金属的深度（趋肤深度）变得可以与全局互连的横截面尺寸比拟甚至更小。例如，1GHz时，铜的趋肤深度约为2μm；随着频率的上升，趋肤深度以频率平方根的速率减小。结果，金属互连上的传导电流密度不再均匀，并且金属阻抗变得与工作频率有关。由于采用常数R、L（直流时的RL）表示片上互连的通常做法没有考虑这种频率相关性，因此不再适用。图8-7a所示为使用Raphal法（一种基于RLC的提取工具）对三条平行互连的横截面电流分布的分析结果。当频率升高时，电流流向互连的表面并远离电流同向的邻近互连。这种非均匀型电流分布在单互连时被称为趋肤效应，而在邻近互连存在感性耦合时为邻近效应。在频率较高时这些效应导致很大的电阻，如图8-7b所示（注意，互连电感仅轻微下降并最终饱和）。

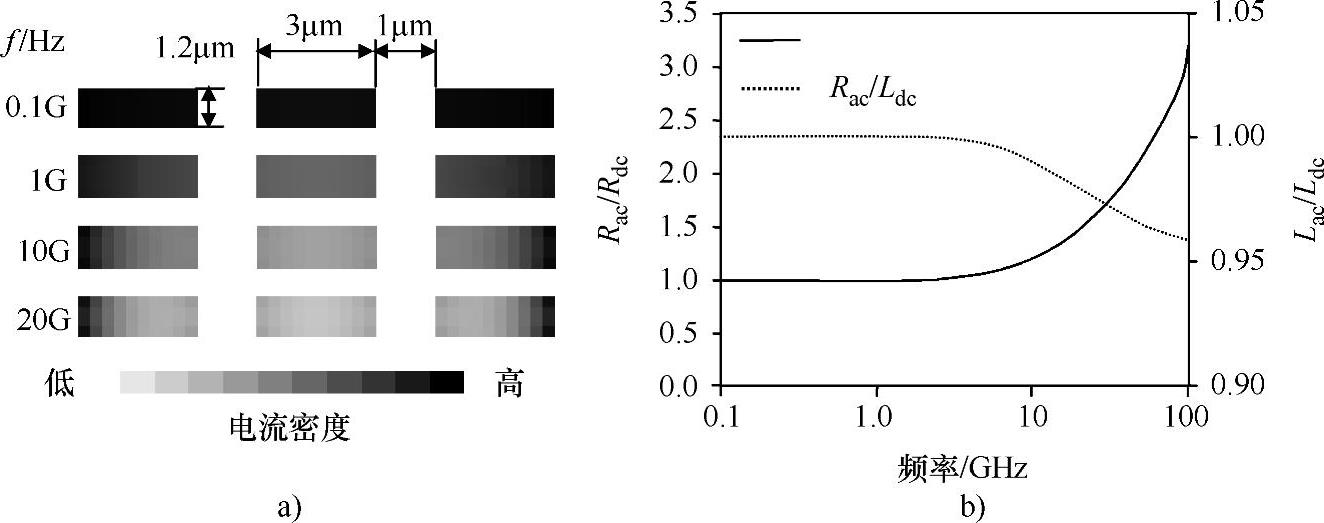
图8-7 R（f）和L（f）的PEEC仿真结果

a）横截面电流密度分布（铜互连厚度=1.2μm） b）R和L的频率相关情况(www.xing528.com)

已有文献报道了很多分析R和L与频率相关效应的方法：采用高频RL值^[26]；预先确定回路RL值^[25]；或者等效电路解析模型^[27]等，对GHz领域的时序进行估计，增大了提取和分析的复杂度。而事实上，采用直流RL和采用R（f）L（f）之间的波形对比显示，所预测出的时延差异却非常小：图8-8a所示为对90nm CMOS工艺^[2]情况下的预测，使用直流RL模型与使用R（f）L（f）模型^[28]所得到时延和上升边非常一致。这个现象的原因可以解释为在对应上升边的电压响应中，感抗ωL占主导：在当前的铜互连工艺下，当开关频率超过几GHz，趋肤效应明显，ωL通常远大于R。因此，在GHz领域，时延对L的变化比对R的变化更敏感。当频率进一步升高时，L仅轻微下降（见图8-7b）；并且R和L与频率的关系相反，又将进一步减小R（f）L（f）对信号时延的整体影响。总之，采用直流RL值对时延进行分析就已经足够了。上升边过后，输出信号慢下来而且电阻在波形的过冲和振铃中起主导作用，造成两个波形具有不同的振铃幅度和周期。

与时延对R（f）L（f）的不敏感性相反，由于高频时电阻值更大，电源线上的L（di/dt）噪声被R（f）L（f）强烈地抑制。如图8-8b所示，使用R（f）L（f）预测得到更小的峰值和更快的衰减。这就意味着，当考虑金属阻抗的频率相关性时，使电源供电稳定所需的去耦电容更小。对图示实例，为了将峰值噪声减小到V_dd的10%以下，直流RL预测需要134pF的去耦电容，而R（f）L（f）的预测值为115pF。考虑了频率相关性，采用更小的电容可以节省超过15%的芯片面积。这一效应很重要，因为对电源稳定性的要求越来越高导致了去耦电容器面积成本的快速增加。因此，在数GHz领域，正确考虑R（f）L（f）有助于减缓这种担心，并提供有效的供电稳定性。

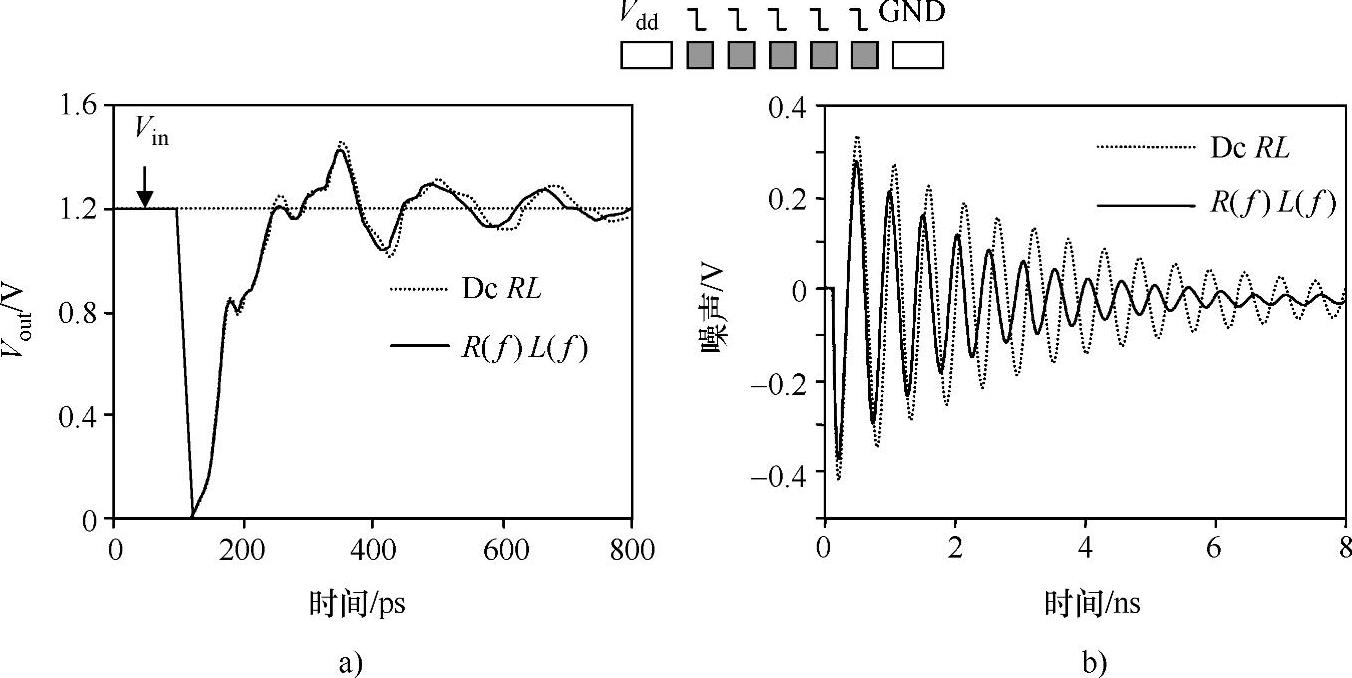
图8-8 R（f）和L（f）对电路性能的影响

a）采用斜坡输入（w=5μm，s=2μm，长度=3mm；w_Vdd=10μm）的输出波形 b）地线上的噪声（对电源线，w=50μm，length=500μm；C_decoupling=50pF；I=100mA）

片上和片外电感的差异 在过去的几十年间，电感一直是板级封装这类片外互连设计中所关注的焦点。尽管对片外设计已经做了大量的关于电感建模方面的工作，但是这些工作不能直接被片上互连采纳，因为片上互连有更复杂的互连环境和不同的几何尺寸。片上和片外互连之间的主要差异可归结如下：

（1）电流返回路径。在片外设计中，接地等位面一般在版图中被设计得很宽大以减小电感（例如，带状线结构）；这些额外的互连并没有给设计增加太大的开销。最终的电流返回路径定义是明确的，因此很容易得到分析电感用的近似公式。相比之下，由于布线资源有限，片上互连一般没有定义明确的电流返回路径。

（2）电阻性损耗。片外互连比片上互连有更大的横截面。它们的损耗小于片上互连并且因此表现出更显著的传输线行为，如波的反射。低损耗传输线理论可以被应用到片外互连分析。然而，片上传输线经常表现为高损耗，从而分析起来更复杂。

（3）布线的复杂性。片上互连布线比片外互连更密集，并且需要将非常大量的邻近互连包括到分析中，才能正确地估计电流返回路径和互连行为。

（4）端接。使用电阻器与互连的特性阻抗[Z₀=（L/C）^1/2]匹配，就比较容易实现片外互连的端接。相比之下，实现理想的片上互连端接极具挑战性，因为片上互连的特性阻抗不是纯电阻性的

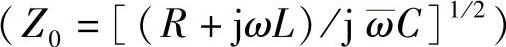
，并且驱动器的尺寸一般是针对时延最小化要求优化过的，它的输出阻抗不可能等于Z₀，并且片上负载的输入阻抗几乎纯粹是容性的。