混合信号集成电路中的器件建模优化

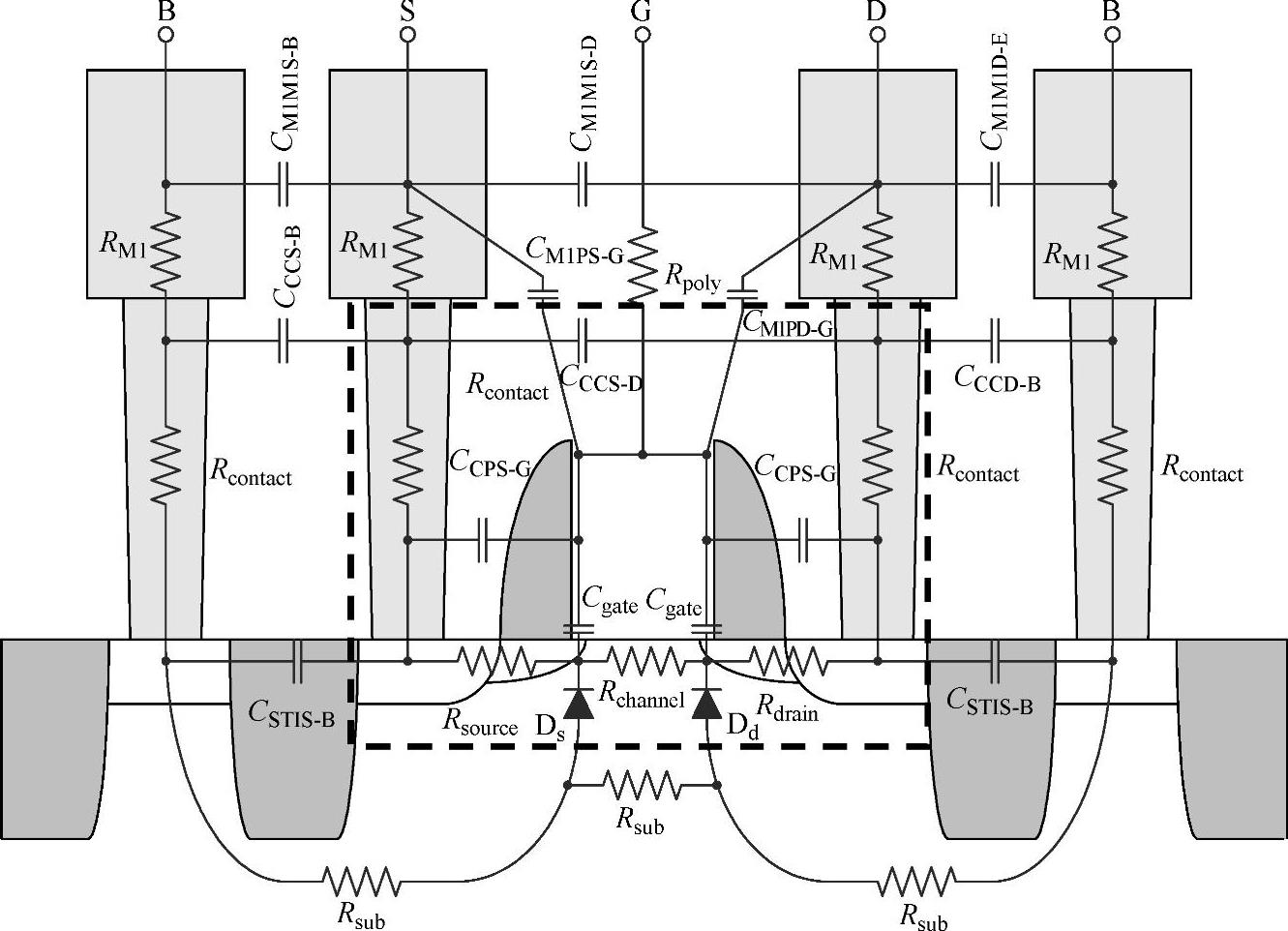
图4-1 晶体管模型

针对下一代工艺的挑战性的设计目标，能够精确反映电路物理特性的器件模型就变得更加复杂。对90nm及尺寸更小的工艺，成功设计混合信号集成电路要求采用精度更高的器件模型。例如相对于0.13μm，除了增加模型的电流参数外，还必须考虑几个在以前工艺中可以忽略的新因素，包括：

●浅槽隔离（STI）应力感应效应

●栅泄漏电流

●栅感应漏电流（GIDL）

●应力感应二极管漏电流

●多晶硅栅耗尽效应

●浅漏源的串联电阻

●负偏温度不稳定性（NBTI）

BSIM3模型已经考虑了上述很多问题，但是这些效应的影响随着尺寸的缩小变得更加显著。图4-1所示为一个包括了几个上述寄生元素的MOS器件截面简图。在先前的工艺中，其中许多元素因为与其他寄生元素（如扩散电容）相比较小而被忽略，但是对更先进的工艺，如0.13μm和小于0.13μm的工艺，它们将不能再被忽略了。建模过程的关键是要明确基本模型中要包括哪些元素，布局前仿真采用的子电路必须包括哪些元素，而在寄生参数提取部分又必须包括哪些元素。图4-1所示器件中，虚线区域代表基本器件模型包括的部分。为了在能够产生合理结果的同时，又能使模型的复杂度最小，关键问题是需要确定哪些参数对器件的性能影响最大。调整关键的设计规则能使一些寄生元素的影响最小，例如增加栅与接触孔的间距。这等效于对同一设计执行了两次设计规则检查，一次是针对设计的数字部分，而另一次则是针对设计的模拟部分。

表4-1总结了模型中通常考虑的各种寄生元件以及基于典型的90nm工艺的数值范围。最右边的一栏列出了相应数值的可能偏差，作为混合信号电路分析中是否需要考虑该寄生参数时参考。该列中的空白栏意味着很难给出其偏差范围，因为他们与特殊的应用有很大关系。

表4-1 器件模型寄生参数和90nm典型工艺的取值范围

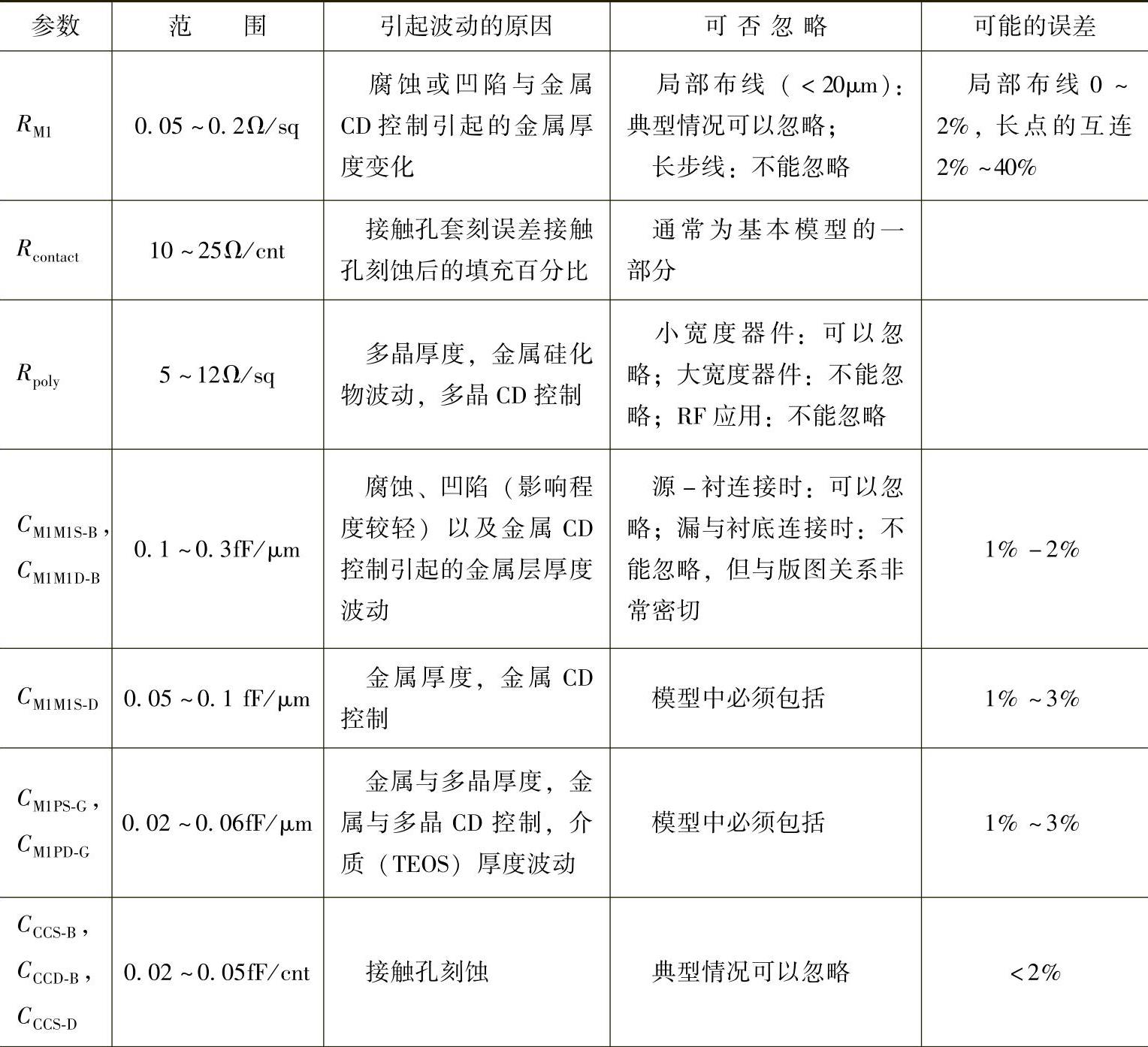
（续）

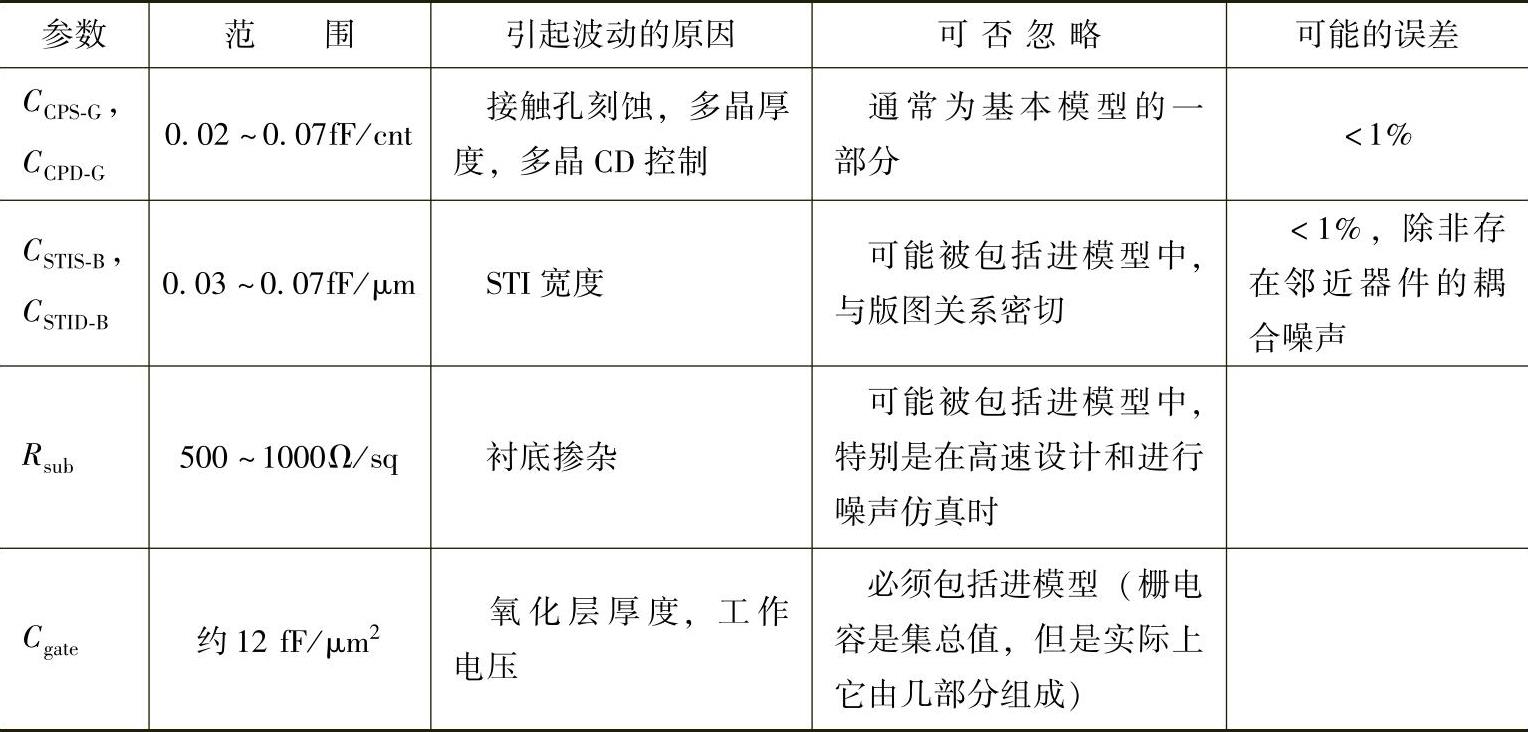
图4-2所示为版图设计后期布线寄生电阻设为0的一个模块中提取的结果与实际测量值之间的误差。从这个模块中测量了多达72个延迟时间，其中2/3的路径出现的误差小于5%。这看起来相当小，但是如果考虑一个工作频率为10GHz的高速时钟数据恢复芯片，其时钟周期仅100ps，因此5%的误差将是5ps，这足以产生时序错误，特别是与其他定时误差源叠加时问题将更加严重。

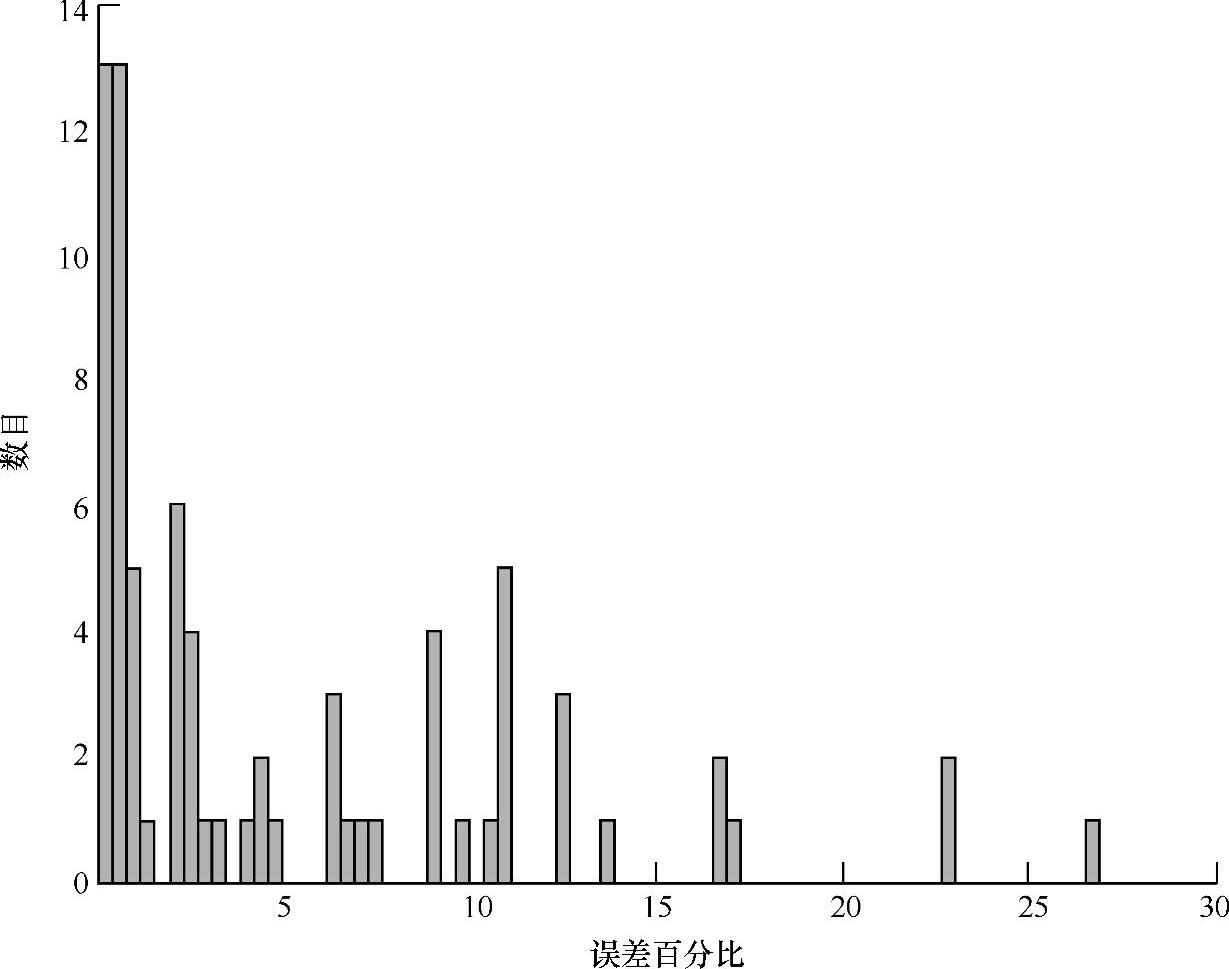
图4-2 90nm工艺情况下忽略金属和多晶电阻导致的误差

图4-3a所示为90nm工艺锁相环电路中高速数字部分的节点电容。大部分节点电容小于5fF，但是有几个电容由于增加了互连寄生电容而变成了重负载。图4-3b中显示的是压控振荡器（VCO）单元节点电容的常用对数。x轴的零点代表1fF；由图可见大部分电容值小于1fF，但是节点电容导致VCO单元振荡频率降低。附加效应包括不希望的与邻近节点的耦合，这将引起很大的相位噪声从而使性能退化。(www.xing528.com)

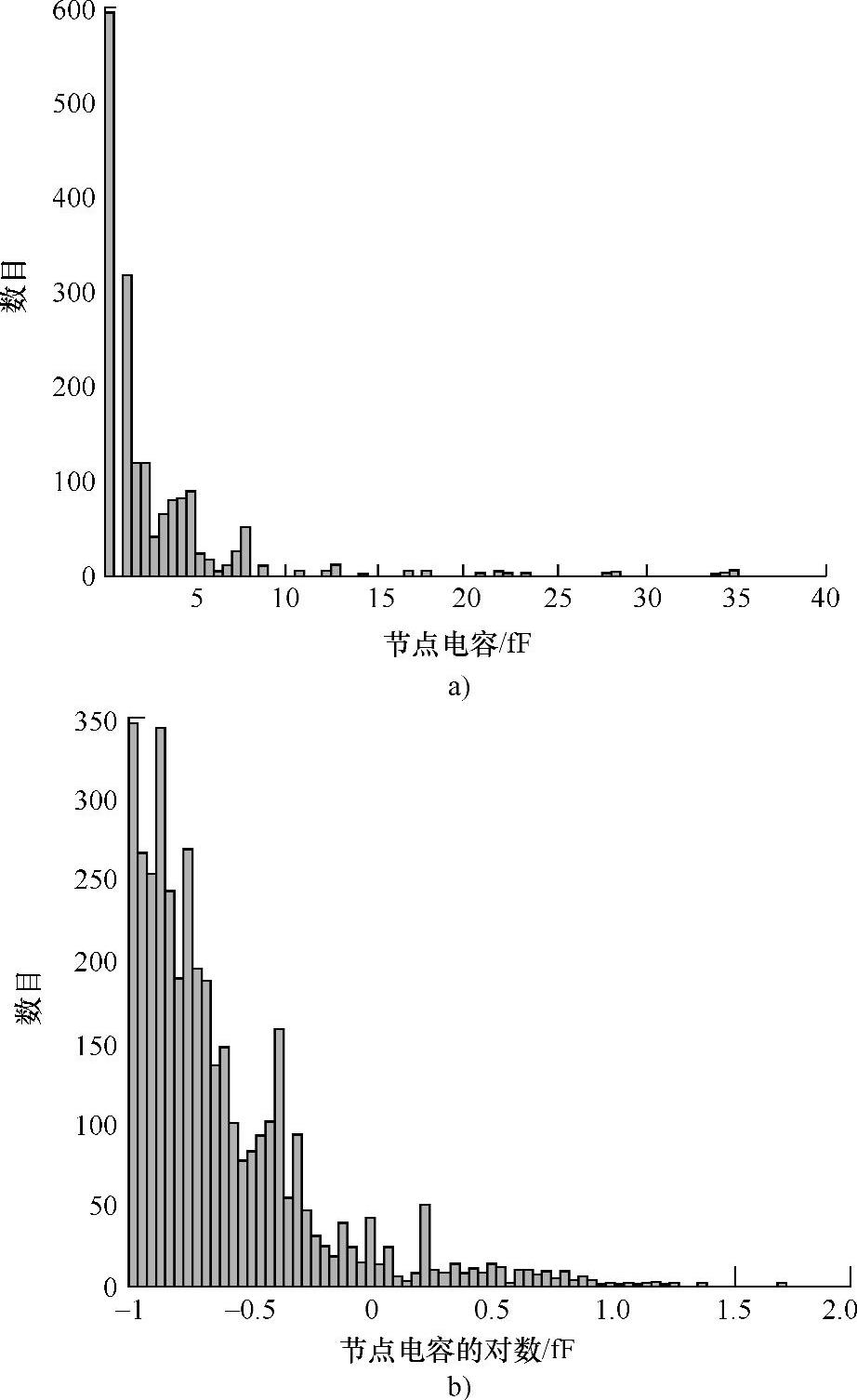
图4-3 采用90nm工艺的锁相环电路中的节点电容

a）高速数字模块的节点电容 b）压控振荡器的节点电容

更新的BSIM4模型考虑了STI应力感应效应和栅泄漏效应。STI应力效应的引入并不影响仿真时间，但是栅泄漏效应将使仿真时间急剧增加。栅泄漏效应与偏置有关，因此在仿真运行期间每个工作点计算均需重新进行估算，而不是只要在仿真开始时计算一次即可。STI应力效应与版图密切相关，这需要了解如何对一个电路进行版图设计，才能在版图设计前的仿真中正确考虑STI应力效应。该应力效应的发生是因为硅和氧化硅的热膨胀系数不同，将导致硅中产生压缩应力^[1，37]。压缩应力会引起沟道中载流子迁移率的变化，如图4-4所示。对较小几何尺寸的器件，两个STI区域之间的间距更小，这个效应将变得更加显著。迁移率可以采用下式表征：

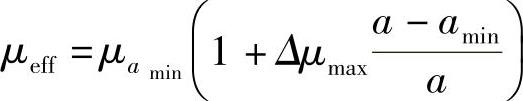
式中，1/a=（1/SA+1/SB）；a_min是工艺设计规则规定的扩散区之间最小间距；μ_amin是在栅到扩散之间的间距为最小值时的迁移率；而Δμ_max是相对于μ_amin的迁移率最大变化值。对PMOS器件，Δμ_max是负值，而对NMOS器件，Δμ_max是正值。随着有源区面积的减小，内建的压缩应力将增加。机械应力的增加导致晶体对称结构受到破坏。明显的形变位能变化可能会导致六重导带的破坏和两重价带的退化。载流子有效质量和能带散射率受到影响，将直接影响迁移率，导致PMOS器件迁移率的净增加以及NMOS器件迁移率的减小。SA与SB的含义如图4-4所示。

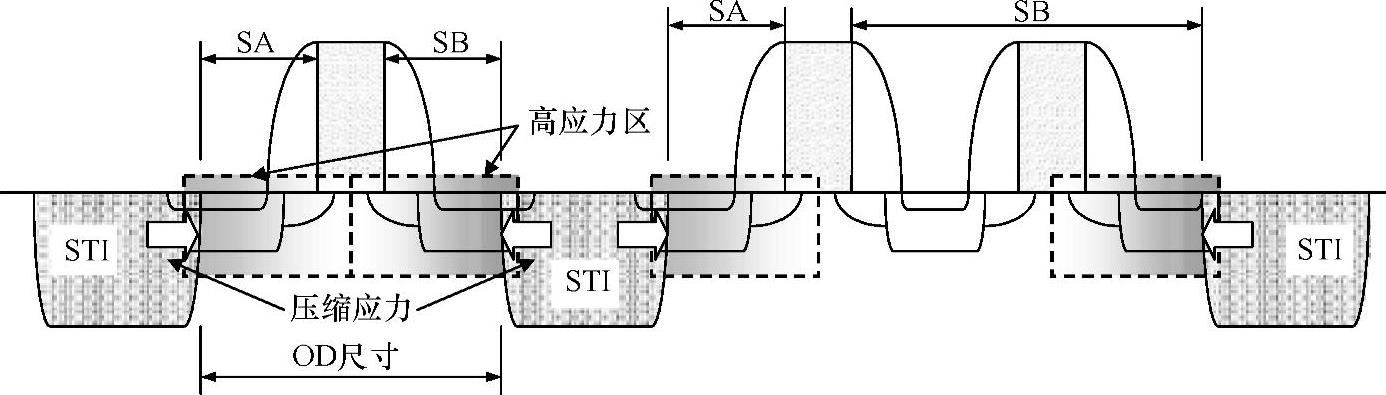
图4-4 单个栅和多指状栅的NMOS晶体管的STI应力

STI外径较小时，STI应力效应将导致空穴迁移率的增加与电子迁移率的减小。图4-5所示为因STI应力效应产生不同类型的I_DS变化曲线。建模是针对图中外径的交叉点。实际电流与模型电流之间的变化程度很重要，因此，模型必须包括STI应力效应以确保仿真结果能很好地反映硅器件特性。从这些数据显然可见，克服这一效应的唯一方式是增加源和漏区的长度，但是将栅分成多个指状也可用来增加总的OD尺寸，如图4-4所示。

在0.15μm（也可能是0.18μm）工艺时，栅泄漏开始成为一个必须考虑的问题。对某些特定的模拟元件，如环路滤波电容，解决问题的方法是不得不使用厚氧器件、多层布线的金属电容或者金属梳状电容来解决。在小于0.13μm的工艺中，其他电路的栅泄漏也必须考虑。90nm工艺中，25℃时，采用V_cc偏压的尺寸为15μm×0.4μm的晶体管，栅泄漏电流将高达5nA。在许多应用中，如简单的数字逻辑中，这么小的电流并不会严重影响电路的运行，但是低功耗设计中，偏置电流非常小，器件工作在亚阈区或非常接近亚阈区，这些泄漏电流将变得非常重要，因此在设计过程中必须加以考虑。在采样-保持电路与多米诺逻辑中也必须同样考虑泄漏电流问题，因为泄漏电流泄放掉电压保持节点的存储电荷，将引起节点电压漂移。另外，栅泄漏电流源于Fowler-Nordthein隧穿，可以被建模为散粒噪声，这是一个可以引起白噪声的随机效应^[38]。这个噪声将影响某些电路（如低噪声放大器和压控振荡器）的整体性能。栅泄漏可以分成三部分^[2]：两边的直接隧穿（Edge Direct Tunneling，EDT）部分（I_gs0与I_gd0）以及栅到沟道的隧穿（I_gc）（见图4-6）。对长沟道器件，栅到沟道的隧穿占主导地位。一般情况下，边界直接隧穿小于栅到沟道的隧穿，因此，随着沟道长度增加，单位泄漏电流将增加。

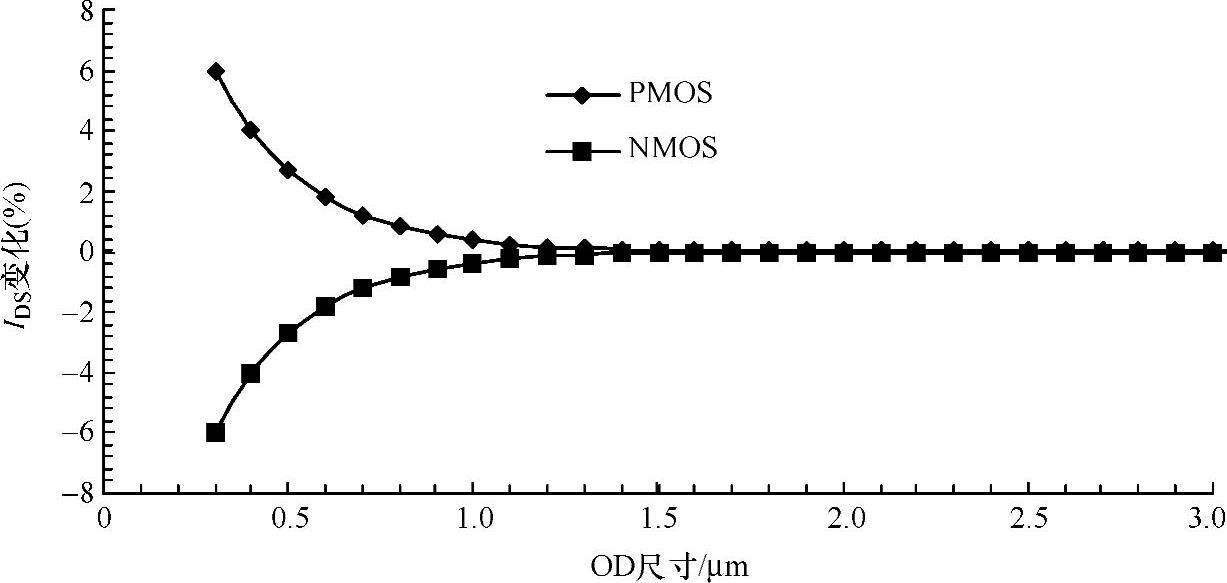
图4-5 先进工艺（0.13μm或更小）I_dsat的变化

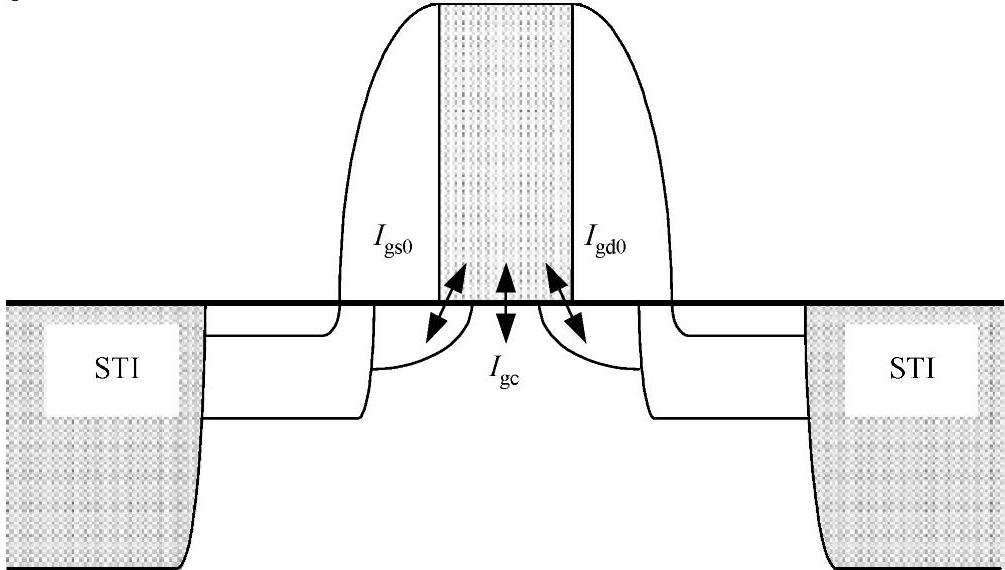
图4-6 栅泄漏的组成

有一段时间，曾采用pocket注入（大斜角注入）方法减小阈值电压下降和穿通。pocket注入的引入对模拟电路有双重影响。第一，它增加了漏感应阈值电压漂移（DITS），这在模拟和混合信号电路中经常使用的较长沟道的器件中更加显著。如果电流镜中器件的源漏电压不匹配，这个效应会在电流镜中增加更多的误差。第二个效应是使输出电阻减小，这是由于阈值电压是漏源电压的函数，并随着漏源电压的增加而不断减小。因为阈值电压对漏源电压有强依赖关系，所以必须考虑使用以下近似方程：

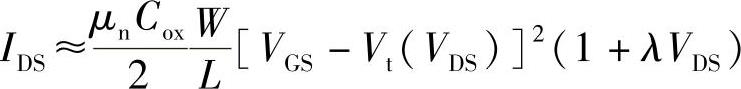
式中，μ_n电子迁移率；C_ox是栅氧化层电容；W是器件宽度；L是沟道长度；V_GS是器件的栅源电压；V_t是阈值电压，它是漏源电压的函数；而λ是器件的沟道长度调制系数。

输出阻抗的减小对模拟电路的影响非常明显，因为这将减小大部分模拟电路的有效噪声隔离。在特定情况下有必要采用“模拟晶体管”，即不使用pocket注入的晶体管。然而，这样做将要求增加附加的掩膜和注入步骤，因此将增加数字CMOS工艺的成本和生产周期。目前基于本章描述的方法仍然有可能设计出鲁棒的电路。

应该考虑的最后一个效应是NBTI效应对长期阈值电压漂移的影响^[3]。本质上，加在PMOS器件上的偏压会导致界面陷阱的产生，从而引起阈值电压的漂移。不像热载流子效应，增加沟道长度并不会缓解这种效应。偏移量依赖于电路配置的细节。开关电路中偏置并不是持续加载的，因此产生的漂移较小，但是仍然会有这种效应发生。对高速时钟电路，较小的占空比变化就会导致错误动作，这仍然是一个存在的问题。阈值电压偏移可能达数十毫伏，这将带来巨大的影响。解决这个问题的一个可能的方法是在工艺角模型中包含阈值电压漂移。