应用绝对值脉冲编码器的优势和使用场景

按二进制制作的编码器在实用上有时出现误码问题。由于多种原因，读码器很难严格处在一条直线上，因此在两个相邻代码的交界处就可能产生误码。如在图6-11中代码“0111”（数7）和代码“1000”（数8）交界处，读码器可能读出0～15中任何一个数的代码。为了消除这一缺点，可采用两种方法。

图6-11 导前—滞后读码法

1.导前—滞后双读法

在按二进制编码的模具上，除了最低位（2⁰位）放置一个读码元件（例如电刷）外，其他各位2¹、2²和2³…都放置两组读码电刷，并依顺序错开L₀/2（L₀为最低位码距），如图6-11所示。这两组读出元件，一组比实际位（以最低位为准）导前（在较大数的方向），另一组则比实际码位滞后（在较小数的方向）。由二进制编码规则可知：①高位码的改变总是在其低一位码由“1”变到“0”时；②高位码的码距是较低一位码距的两倍。因此，当最低位电刷在“0”的左右极限范围内，导前电刷的读数始终是正确的，而滞后电刷则可能处于高位的不确定的边界上。同理，当最低电刷处于“1”的两个极限位置之中时，次低位（2¹）的滞后电刷始终处在正确位置。如此类推，可得读码规律的逻辑关系。利用低位码的状态来确定高一位码，当低位为“0”时，读高一位导前值，而当低位为“1”时，读滞后值。在图6-11中，按这样规律读出“01010”的二进制码，其中黑点表示有效电刷（读出），空心圆点是无效电刷，箭头方向表示判定顺序。图6-12所示是按上述规律读码的逻辑电路。这种读法安排可以保证误码为最低位的一个单位码。

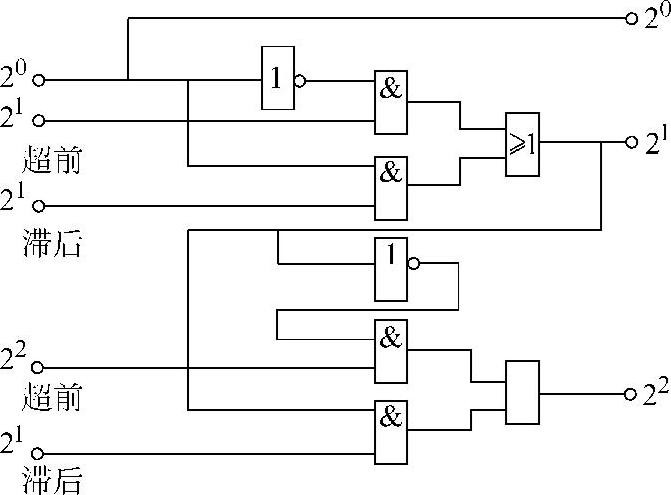
图6-12 导前—滞后判读逻辑图

2.格雷循环码

上面所提到的二进制码属于有权代码，每一个码位上都有相应的权。从最低位开始，码权分别为l、2、4、8…，因此，码位越高，误码的影响越大。格雷码是按一定规则编制出的变权代码，即从二进制的角度看，各个码位上的权是不固定的，但它有两个主要特征：①码（0与1的组合系列）与数（按十进制或二进制）之间有内在的一一对应关系；②相邻两数之间只有一个码位发生变化，在任何码位的边界上由于“0”与“l”竞争产生误码时，它们所代表的数（十进制）只变化最小的单位“1”，因此，格雷码的误码始终保持为最小单位数。(www.xing528.com)

格雷码可以直接由二进制码形成，将二进制B（b₇…b₀）变为格雷码的规则如下：

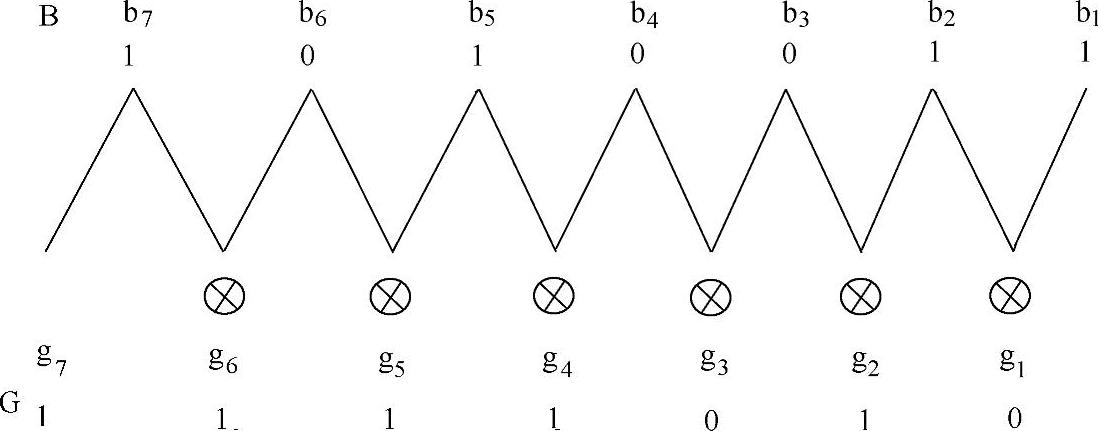
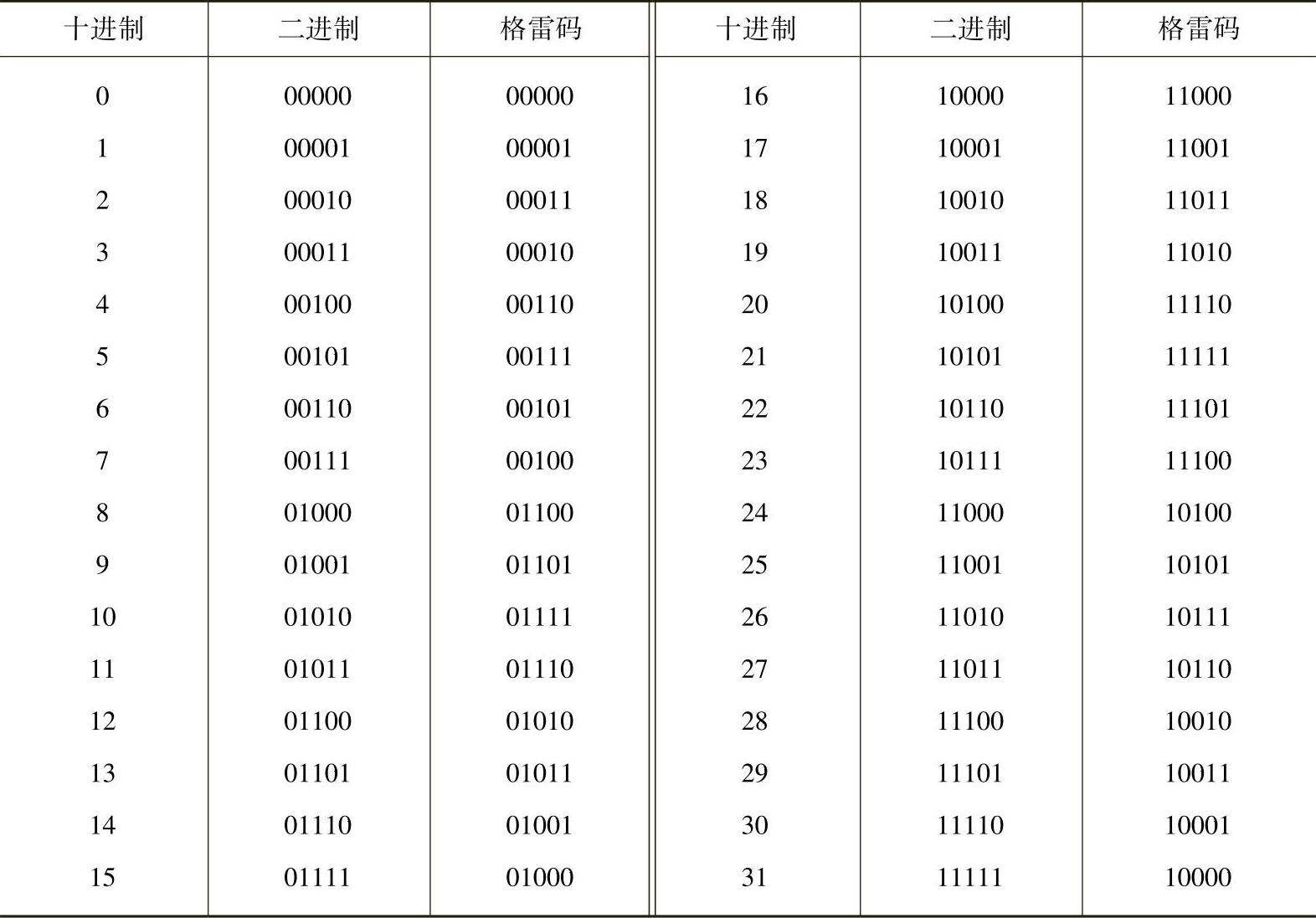
其中，表示按位加，实际上是将二进制码右移一位与其本位作不进位加法。将格雷码变换为二进制码时，其规律是：二进制的最高位与格雷码相同，次高位则视格雷码的次高位和最高位而定，前（最高位）“0”后（次高位）保，前“1”后反，如此类推下去，可得二进制码。图6-13表示5位格雷码编码器，表6-4为相应的数码变换表。

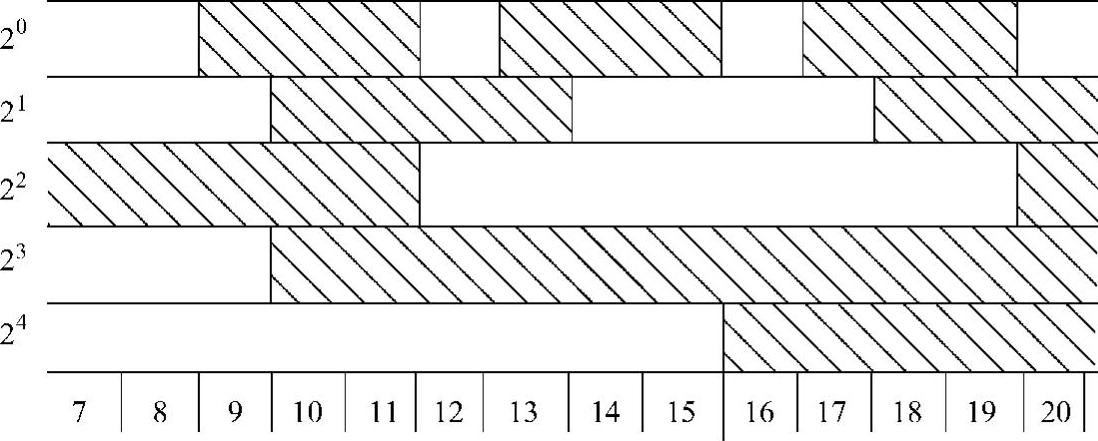
图6-13 5位格雷码编码器

表6-45位格雷码数码变换表