改进DDA插补质量的实用方法

1.数字积分法插补的进给速度分析

DDA插补的特点是控制脉冲源每产生一个脉冲，就作一次积分运算。每次运算中，X方向平均进给的比率为x/2ⁿ（2ⁿ为累加器容量），而Y方向的进给比率为y/2ⁿ，所以合成的轮廓进给速度为

式中 δ——脉冲当量（mm）；

f_g——插补迭代控制脉冲源频率；

L——程编的插补段的行程，直线插补段时为直线长度，即；圆弧插补段时为圆弧半径，即L=R。

插补合成的轮廓速度与插补迭代控制源虚拟速度（即假定每发一个插补控制脉冲后坐标轴走一步）的比值称为插补速度变化率，其表达式为

上式表明速度变化率与程序段的行程L成正比。当插补迭代控制源脉冲频率f_g一定时，行程长，脉冲溢出快，进给快；行程短，脉冲溢出慢，进给慢。数据段行程的变化范围在0～2ⁿ间，所以合成速度的变化范围是v=（0-1）v_g，这种变化在实际加工中是不允许的。

在DDA硬件插补中，常常采用“左移规格化”的措施来稳定速度。

2.进给速度的均匀化措施——左移规格化

（1）DDA直线插补的左移规格化 直线插补时，在被积函数数据送入寄存器时，进行左移，直到X或Y寄存器有一个最高位为1时左移停止，转入插补运算。由于左移，迫使数据段的行程增大到充分利用寄存器容量的程度，从而使插补溢出速度基本稳定。左移的同时，为了使发出的脉冲总数不变，就要相应地减少累加次数。在硬件系统中，常采用使终点计数器右移同样位数的方法来实现。

由于左移规格化的结果，使寄存器中数值变化范围小，即缩小了L值的范围。其可能的最小数是：

x=2^n-1，y=0

L_min=x=2^n-1

最大数是：

式中，n为寄存器字长，故合成的速度最大、最小值为

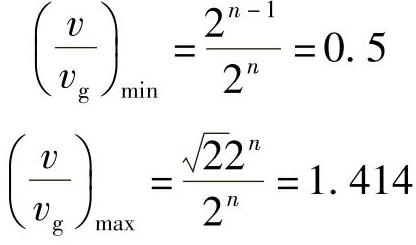
即合成速度变化范围为v=（0.5～1.414）v_g，比未采取左移规格化时的速度大为稳定。

（2）DDA圆弧插补的左移规格化 为提高圆弧插补的速度均匀性，在圆弧插补时也可采用左移规格化的方法。其原理与前述的直线插补左移规格化相似，但要注意以下三个问题：

1）圆弧插补的左移规格化，是将两个被积函数同时左移，使其中至少有一个寄存器的内容的次高位为1。这是因为当一个坐标进给，而要修正另一个被积函数时，防止在第一次修正被积函数时使其溢出。例如，在加工第一象限顺圆，圆弧的起点坐标值相同时，若左移规格化是最高位为1，先将X方向累加，其结果产生溢出，X方向进给一步，Y方向被积函数加上一个增量，这样Y方向的被积函数还未参加累加计算就有可能溢出，导致Y方向的第一次累加错误。

2）要求被积函数寄存器的容量是最大被积函数的两倍，其原因也是因为每次累加有溢出时要修正被积函数，防止在修正时被积函数本身产生溢出。例如，当寄存器为8位二进制时，最大坐标值为127。

3）由前述插补原理可知，当有一个坐标进给时，要修正另一坐标的被积函数。例如，当有Δx时，J_VY（x）加或减Δx，此时Δx为1，经进行左移规格化后，Δx就不是1了。其解决方法是，左移规格化前，先设一个寄存器存放Δ，并使其预置为1，在被积函数左移一位的同时，将Δ左移一位。在修正被积函数时，不再是加1或减1，而是加Δ或减Δ。

3.减少插补误差的方法——累加器预置数

产生误差的原因是插补采用步进式，在一步（一个脉冲当量距离）的范围内，用切线代替圆弧是有误差的，而且下一步又在前一步的基础上判断新的走向，最后必然产生误差，积分器圆弧插补误差大于一个脉冲当量，小于或等于两个脉冲当量。减少插补误差的方法有：

（1）减少脉冲当量 则误差的几何尺寸减小，但信息量变大。寄存器的容量需加大，而且欲获得同样的机床进给速度，需要提高运算速度，这些都是不好的。

（2）累加器中预置0.5 即被积函数寄存器中的数如果存的是终点坐标值x_Z或y_Z，如存的是整数时，则小数点设置在寄存器最低位后，即预置2ⁿ/2，如n=5，则2ⁿ/2=2⁵/2=32/2=16，

即 1 0 0 0 0

若寄存器中存的数是x_Z/2ⁿ，即存的是小数，小数点位于数码最高位前，如(www.xing528.com)

1 0 0 0 0

即

16/2⁵=16/32=0.5

前者累加∑δ_X超过2ⁿ时才有溢出脉冲，而后者累加∑δ_X超过1时便有溢出脉冲。

（3）下面分直线与圆弧两种情况加以分析

1）直线插补时。

【例3-6】如有一直线OZ位于第一象限，起点在坐标原点，终点Z坐标为x_Z=8，y_Z=2，不预置数时累加过程见表3-10，插补轨迹见图3-18。

表3-10 不预置数时累加过程（直线插补时）

预置0.5时累加运算过程如表3-11所示，插补轨迹见图3-19，比较图3-18及图3-19，后者误差显著减小。

表3-11 预置0.5时累加运算过程

（续）

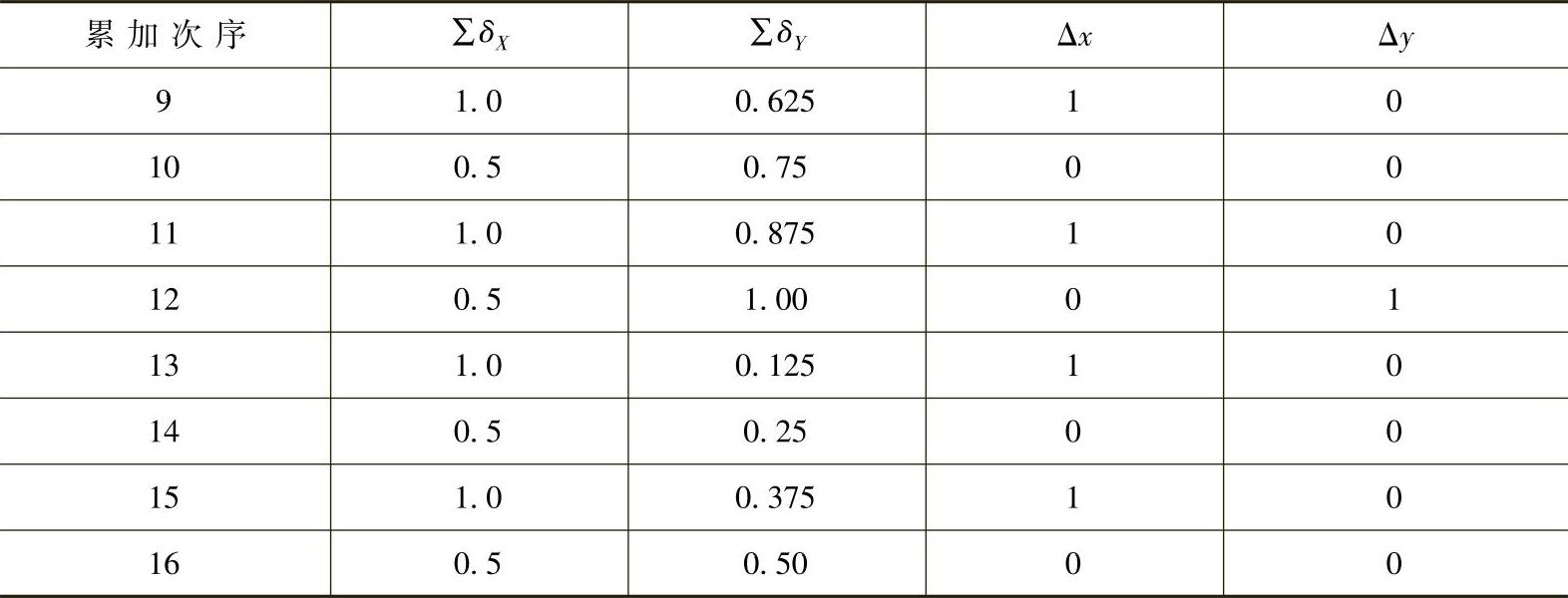
图3-18 不预置数时插补轨迹

图3-19 预置0.5时插补轨迹

2）圆弧插补时。

【例3-7】在XY平面内有一逆时针走向的圆弧QZ，圆弧起点Q（5，0），终点Z（0，5），试用数字积分法圆弧方式插补之。不预置数时累加过程见表3-12。预置，累加运算过程见表3-13，插补轨迹如图3-20所示。

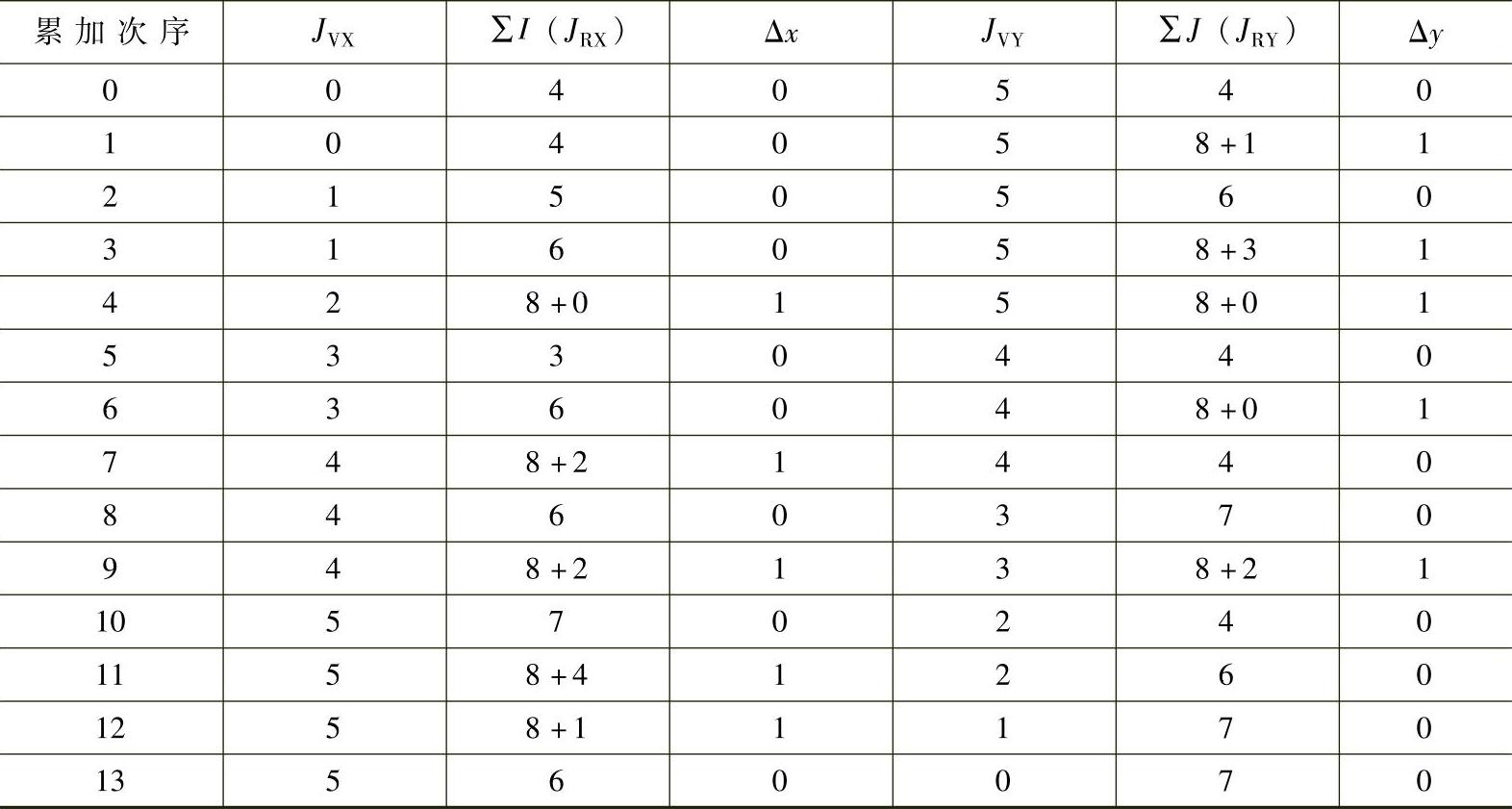
表3-12 不预置数时累加过程（圆弧插补时）

（续）

如果终点判别计数器是设一个总的计数器，那么就会使Y轴多走一步，产生插补误差，因为没有给累加器预置数（累加器和寄存器容量的一半和全部），往往会使小坐标轴先到达终点后没能停止进给而继续走步。克服此种情况发生的办法就是给每个坐标轴分别设置终点判别计数器，谁先到达终点就停止插补，进入等待状态。所有轴都到达终点，插补结束。

图3-20 预置数的插补轨迹

表3-13 累加运算过程