数字积分法优化圆弧插补

1.圆弧插补原理

以第一象限逆圆为例。如图3-15所示，设圆弧的圆心在坐标原点，起点为A（x₀，y₀），终点为B（x_e，y_e），半径为r。圆的参量方程可表示为

x=rcost

y=rsint

对t微分求得x、y方向上的速度分量

写成微分形式

dx=-ydt

dy=xdt

用累加和来近似积分

这表明圆弧插补时，X轴的被积函数值等于动点Y坐标的瞬时值，Y轴的被积函数值等于动点X坐标的瞬时值。与直线插补比较可知：

1）直线插补时为常数累加，而圆弧插补时为变量累加。

2）圆弧插补时，X轴动点坐标值累加的溢出脉冲作为Y轴的进给脉冲，Y轴动点坐标值累加溢出脉冲作为X轴的进给脉冲。

3）直线插补过程中，被积函数值x_e及y_e不变。圆弧插补过程中，被积函数值y及x，必须由累加器的溢出来修改。圆弧插补X轴累加器初值存入Y轴起点坐标y₀，Y轴累加器初值存入X轴起点坐标x₀。

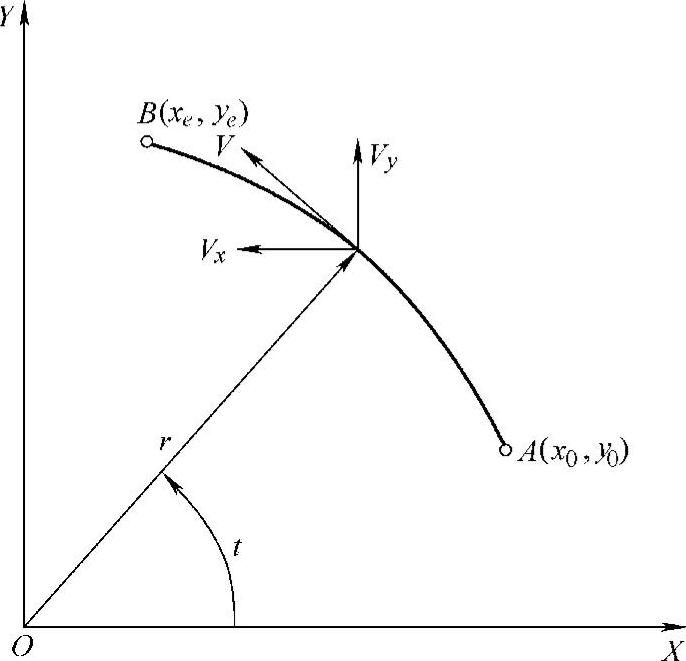
图3-15 圆弧插补速度方向

对于累加过程来讲，累加进位的速度和连减借位的速度是相同的，所以X轴被积函数的负号可忽略，两个轴的插补都用累加来进行。通常累加器初值都置为累加器容量的一半，这样二者的差别可以完全消除，并可改善插补质量。

因为在用数字积分法进行圆弧插补时两轴不一定同时到达终点，可以采用两个终点判别计数器JX及JY。各轴分别判别终点，进给一步减1，判终计数器减为0该轴停止进给。两轴都到达终点后停止插补。

与逐点比较法类似，将进给方向的正负直接由进给驱动程序处理，而用动点坐标的绝对值进行累加，则插补程序将相对简单。插补程序的任务，一是进行累加，二是根据溢出调用进给驱动程序和修改动点坐标值（被积函数值）。

2.DDA圆弧插补器(www.xing528.com)

由第一象限逆圆加工的DDA插补表达式可得到其圆弧插补器框图，如图3-16所示。图中，J_VX为X方向的被积函数寄存器，J_VY为Y方向的被积函数寄存器，J_RX是X向的积分累加器，存放X向积分结果的余数；J_RY是Y向的积分累加器，存放Y向积分结果的余数；ΔX为Y向积分结果的溢出（进位），ΔY为X向积分结果的溢出（进位）。其工作过程如下：

1）运算开始时，X和Y被积函数寄存器中分别存放X、Y的初值X₀、Y₀。

2）X轴被积函数寄存器累加得到的溢出脉冲发到Y方向，而Y轴被积函数寄存器累加得到的溢出脉冲则发到-X方向。

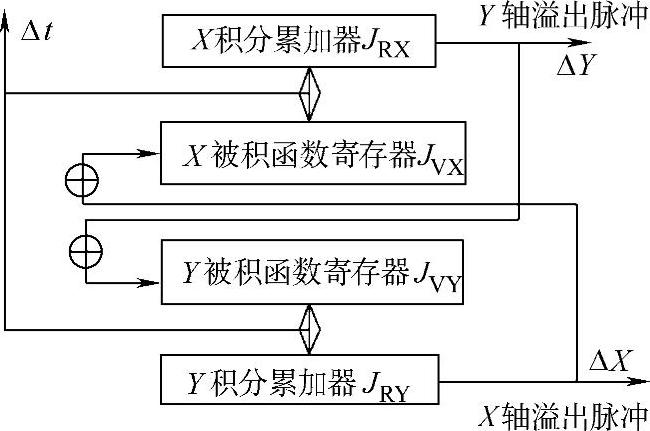
图3-16 第一象限逆圆加工的 DDA插补器框图

3）每发出一个进给脉冲后，必须将被积函数寄存器内的坐标值加以修正。其修正方法是：当X方向发出进给脉冲时，使X轴被积函数寄存器的内容减1，这是因为X进给一步时，X坐标减小；当Y方向发出进给脉冲时，使Y轴被积函数寄存器的内容加1，这是因为Y进给一步时，Y坐标增大。即使被积函数寄存器内随时存放着坐标的瞬时值。

3.其他象限圆弧的DDA插补

其他象限圆弧插补的原理与第一象限逆圆插补类似。其不同之处有：进给方向不同；被积函数的修正不同。因为插补时用坐标的绝对值，坐标值的修改要看动点运动使该坐标绝对值是增还是减来确定是加1修改还是减1修改。圆弧插补的坐标修改及进给方向如表3-8所示。

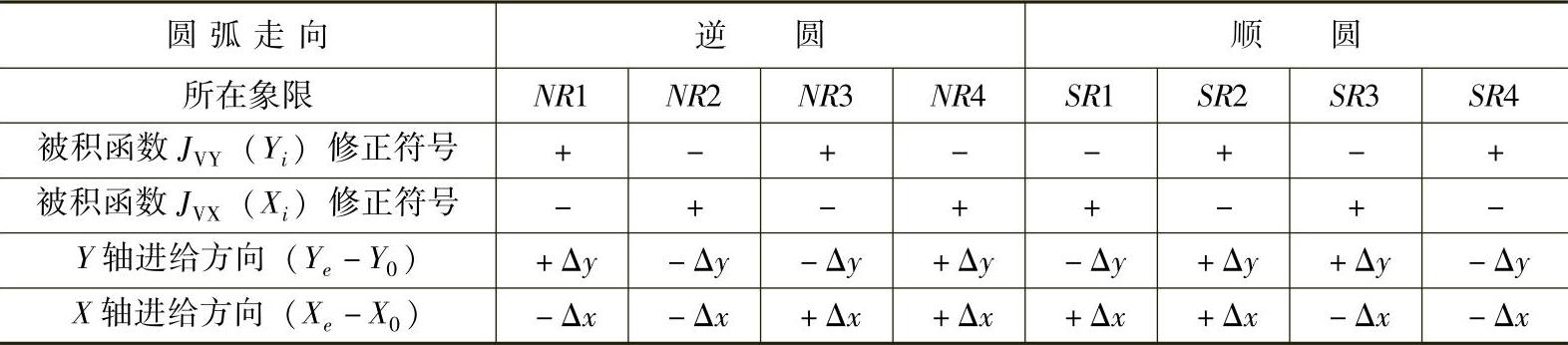
表3-8中共有八种线型，分别为顺圆第一、二、三、四象限（符号为SR1、SR2、SR3、SR4）和逆圆第一、二、三、四象限（符号为NR1、NR2、NR3、NR4）。“+”号表示修正被积函数时该被积函数加1，“-”号表示修正被积函数时该被积函数减1。+Δx表示在X的正向进给，-Δx表示在X的负向进给，+Δy表示在Y的正向进给，-Δy表示在Y的负向进给。被积函数值和余数值均为无符号数，即按绝对值处理。

表3-8 圆弧插补坐标修改及进给方向

4.圆弧插补过程举例

【例3-5】设加工第一象限逆圆弧，其圆心在原点，起点A坐标为（6，0），终点B的坐标为（0，6），累加器为三位，试用数字积分法插补计算，并画出走步轨迹图。

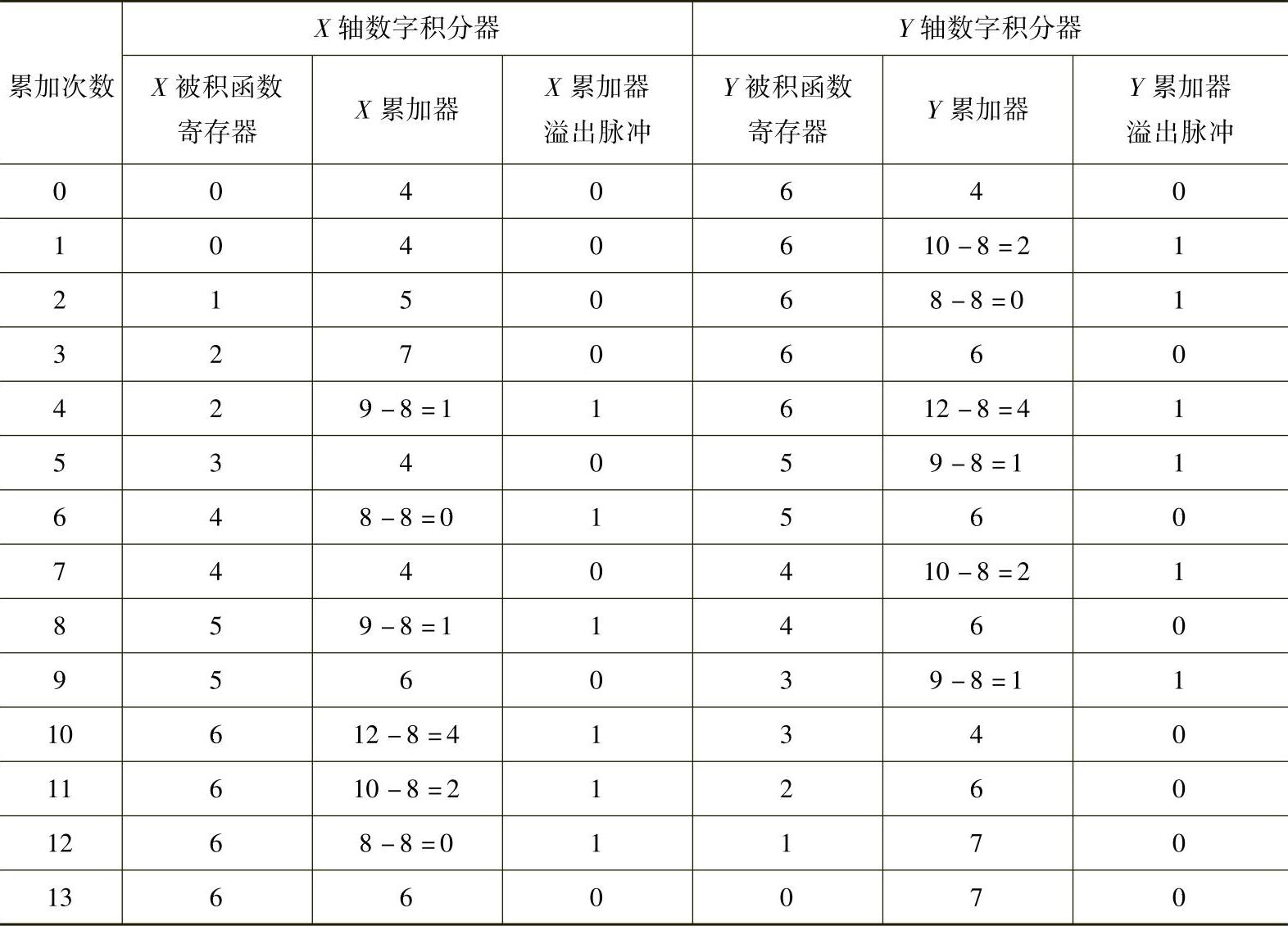
插补计算过程如表3-9所示。为加快插补将两个累加器的初值置成容量半数。走步轨迹如图3-17所示。

关于数字积分法圆弧插补的程序实现略。

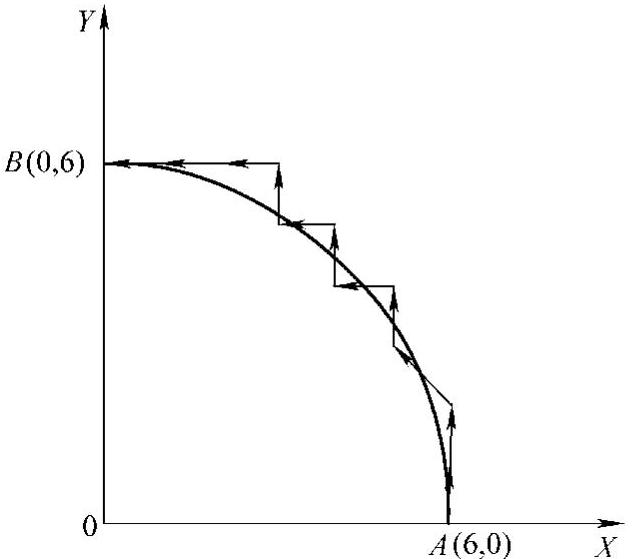
图3-17 数字积分法圆弧插补走步轨迹

表3-9 数字积分法圆弧插补计算过程