数字积分法直线插补优化方案

1.直线插补原理

设在平面中有一直线OA，其起点为坐标原点O，终点为A（x_e，y_e），则该直线的方程为

将式（3-7）化为对时间t的参量方程

x=Kx_et

y=Ky_et （3-8）

式中 K——比例系数。

式（3-8）对参数t求微分得

dx=Kx_edt

dy=Ky_edt （3-9）

对式（3-9）进行积分可得x、y

上式积分用累加的形式表达近似为

式中Δt=1，写成近似微分形式为

Δx=Kx_eΔt

Δy=Ky_eΔt

动点从原点出发走向终点的过程，可以看做是各坐标轴每隔一个单位时间Δt，分别以增量Kx_e及Ky_e同时对两个累加器累加的过程。当累加值超过一个坐标单位（脉冲当量）时产生溢出，溢出脉冲驱动伺服系统进给一个脉冲当量，从而走出给定直线。

若经过m次累加后，x和y分别到达终点（x_e、y_e），即下式成立：

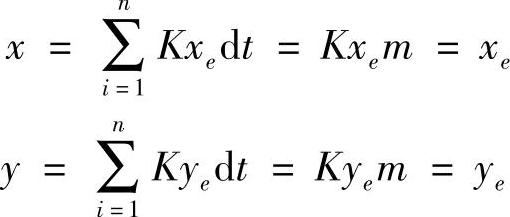
由此可见，比例系数K和累加次数之间有如下的关系：

Km=1，即m=1/K

K的数值与累加器的容量有关。累加器的容量应大于各坐标轴的最大坐标值，一般二者的位数相同，以保证每次累加最多只溢出一个脉冲。设累加器有n位，则

K=1/2ⁿ

故累加次数

m=1/K=2ⁿ(www.xing528.com)

上述关系表明，若累加器的位数为n，则整个插补过程要进行2ⁿ次累加才能到达直线的终点。

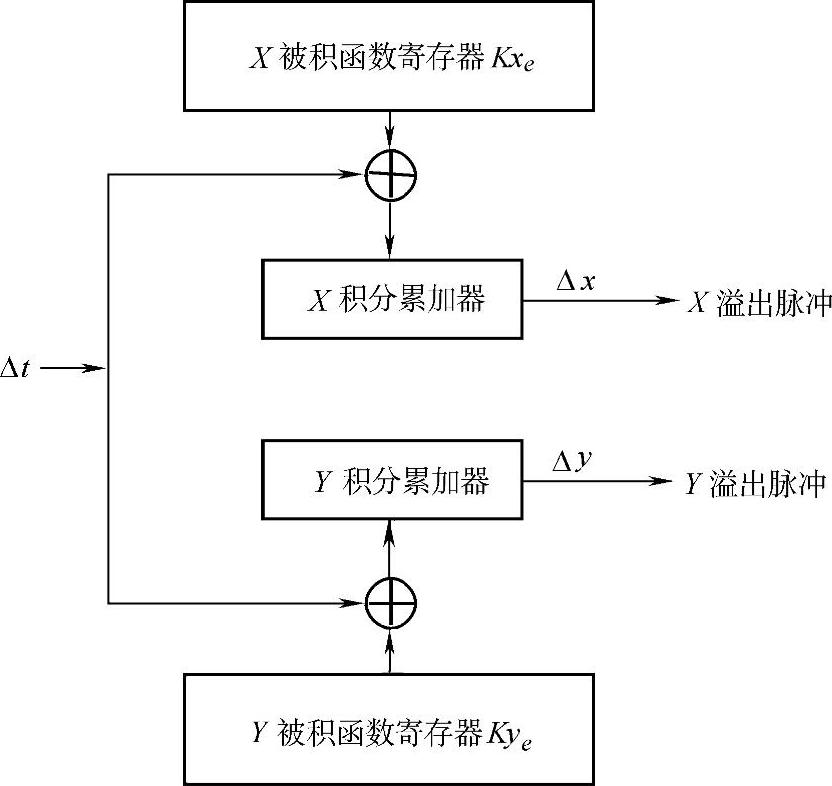
图3-13 平面直线的插补运算框图

因为K=1/2ⁿ，n为寄存器的位数，对于存放于寄存器中的二进制来说，Kxe（或Ky_e）与x_e（或y_e）是相同的，可以看做前者小数点在最高位之前，而后者的小数点在最低位之后。所以，可以用x_e直接对X轴累加器累加，用y_e直接对Y轴的累加器累加。

图3-13为平面直线的插补运算框图。它由两个数字积分器组成，每个坐标轴的积分器由累加器和被积函数寄存器组成。被积函数寄存器存放终点坐标值。每隔一个时间间隔Δt，将被积函数的值向各自的累加器中累加。X轴的累加器溢出的脉冲驱动X轴走步，Y轴累加器溢出脉冲驱动Y轴走步。

当累加器和寄存器的位数长而加工较短的直线时，就会出现累加很多次才能溢出一个脉冲的情况，这样进给速度就会很慢，影响生产率。为此，可在插补累加之前时将x_e、y_e同时放大2^m倍提高进给速度。一般将X轴及Y轴被积函数寄存器同时左移，直到其中之一的最高位为1为止。此过程称为左移规格化。这实际是放大了K值，从直线参数方程可知，K变大后方程仍成立，只是加快了插补速度。必须注意的是，这时到达终点的累加次数不再为2ⁿ，不能用此来判别终点。可以用与逐点比较法相同的办法来做终点判别。即设一个判终计数器，其初值为各轴走步数之和，每当累加器溢出一个脉冲，判终计数器减l。判终计数器减为0，加工结束。也可以各轴分别设一个判终计数器，初值存入相应轴的走步数，该轴进给一步，相应计数器减1，减为0该轴停止进给。所有判终计数器减为0到达终点。

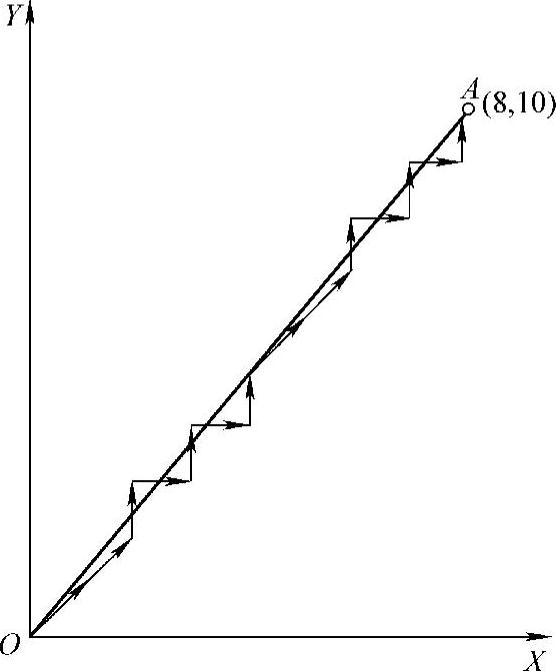
图3-14 数字积分法直线插补走步轨迹

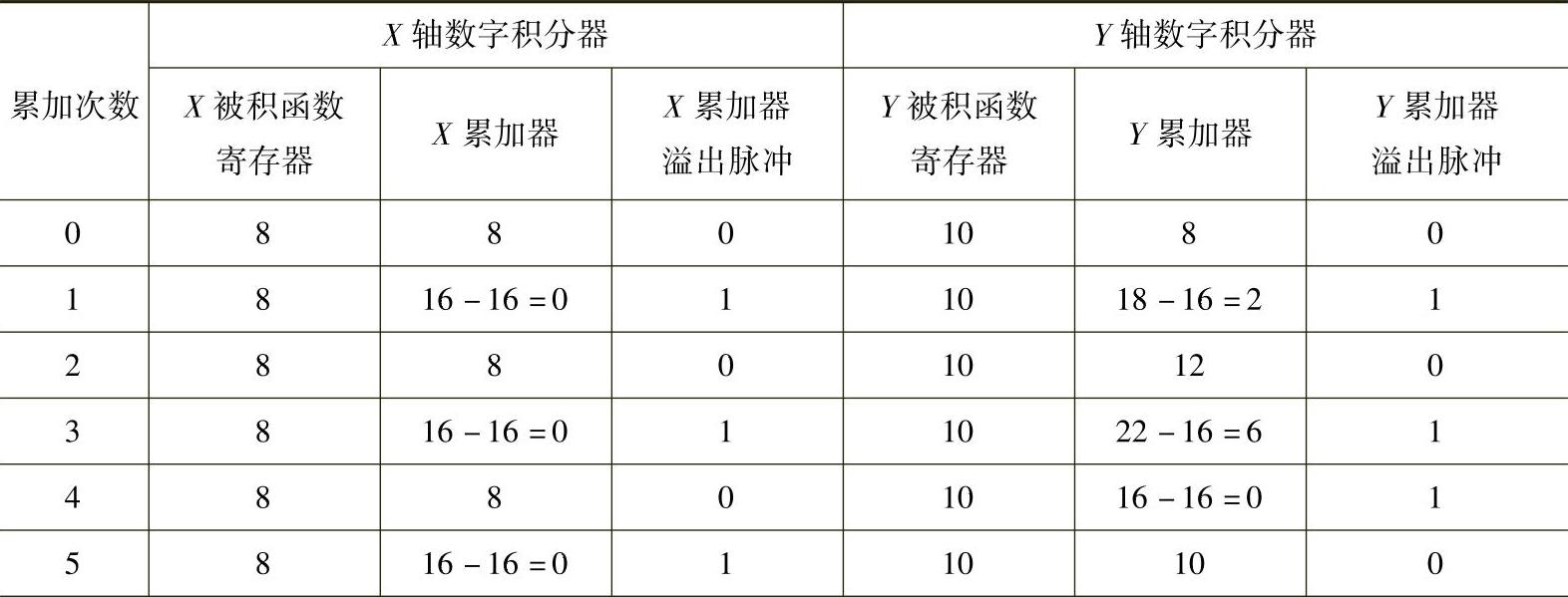
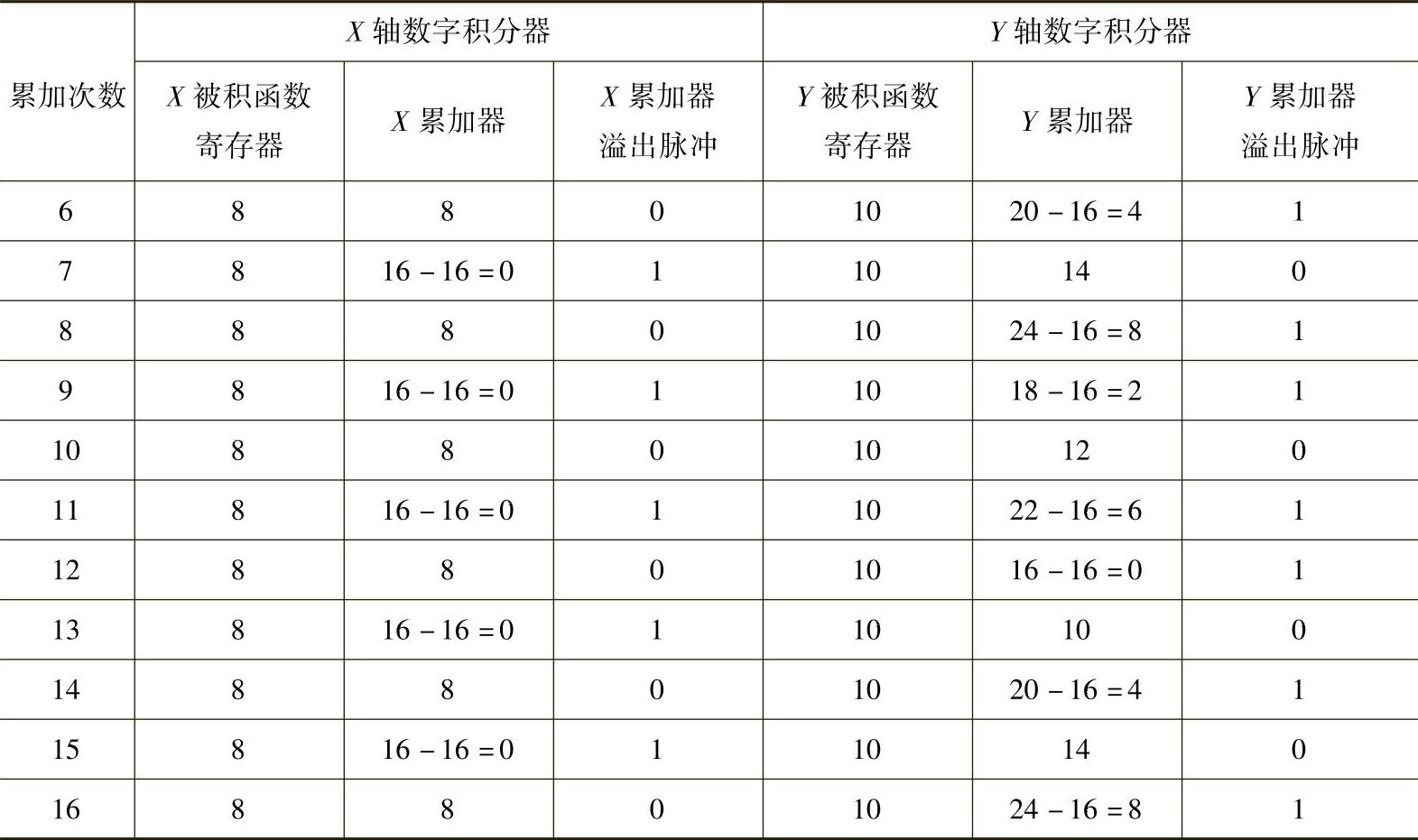
表3-6 直线插补计算过程

用与逐点比较法相同的处理方法，把符号与数据分开，取数据的绝对值作被积函数，而以符号作进给方向控制信号处理，便可对所有不同象限的直线进行插补。

2.直线插补计算举例

【例3-3】设有一直线OA，起点为原点O，终点A坐标为（8，10），累加器和寄存器的位数为4位，其最大容量为2⁴=16。试用数字积分法进行插补计算并画出走步轨迹图。直线插补计算过程见表3-6，为加快插补，累加器初值置为累加器容量的一半。直线插补走步轨迹如图3-14所示。

（续）

3.空间直线插补

（1）空间直线插补原理 数字积分法的优点是可以对空间直线或多维线型函数进行插补，从而可以控制多坐标联动。因为曲面可以由空间曲线组成，空间曲线可以用空间直线来逼近，所以空间直线插补应用较多。多维线性函数的运动轨迹不一定是直线。例如，空间直线插补法可用于三维线性函数插补，若此函数中有一个变量是转角，走出来的运动轨迹也就不是直线了。

空间直线的插补有三个积分器，X轴被积函数为直线终点的X坐标值x_e，Y轴的被积函数为直线终点的Y坐标值y_e，Z轴积分器的被积函数为直线终点的Z坐标值z_e。每进行一次插补，对三个积分器积分，即累加，哪个轴的累加器有溢出则该轴进给一步。

空间直线的终点判别可采用与平面直线相似的方法，可以每个轴各设一个终点判别计数器，分别进行终点判别，三轴都到终点，则插补结束。因为各轴可能不同时到终点，先到终点的轴可能多走出一个脉冲来，使终点坐标产生误差，在增量系统中此误差可能积累下来。各轴分设判终计数器可克服这个缺点。

（2）空间直线插补举例

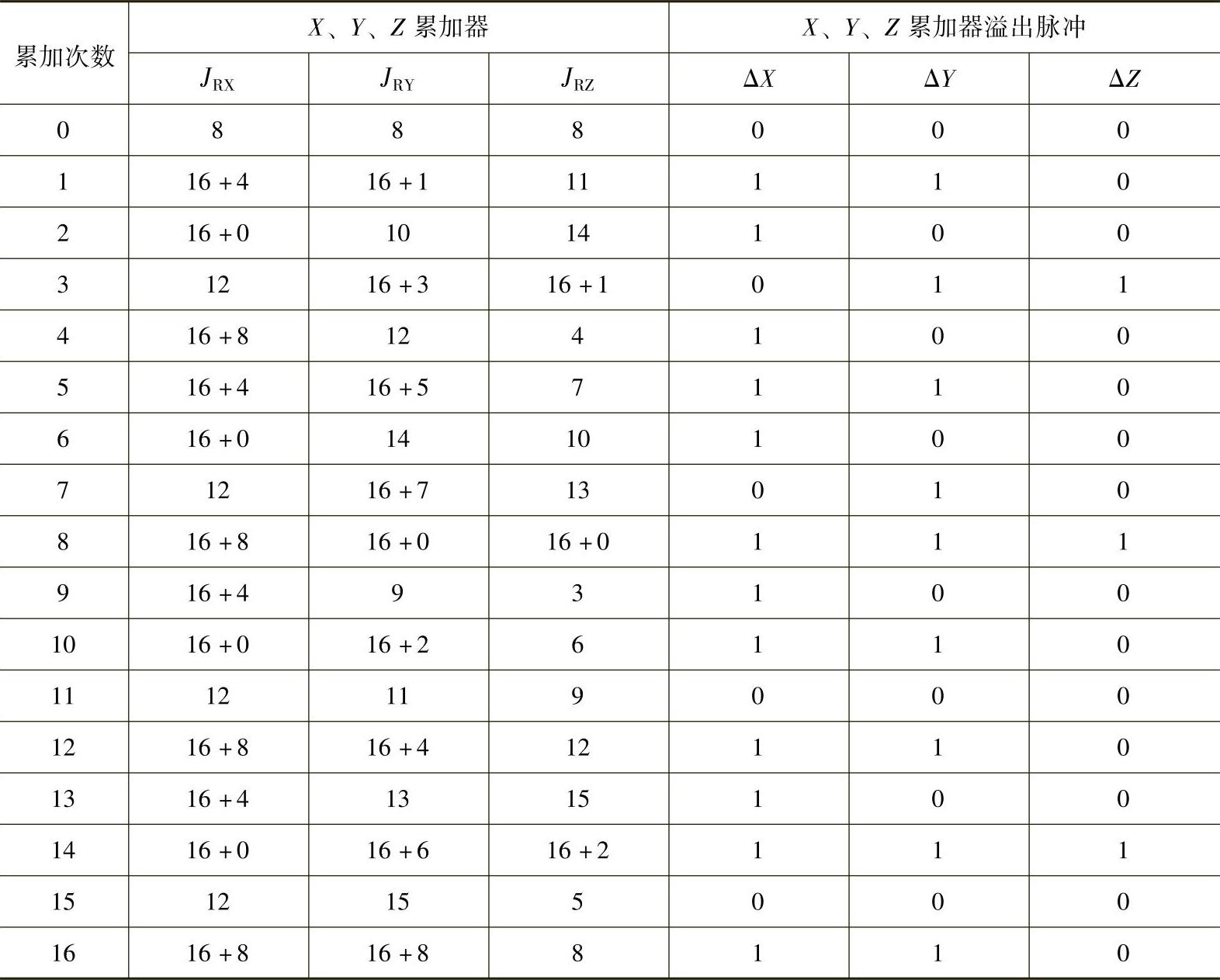
【例3-4】有一空间直线OZ，起点在坐标原点，终点Z的坐标为X_Z=12，Y_Z=9，Z_Z=3。试用数字积分法插补之。

解：设寄存器为四位，容量为2⁴=16，为减少误差，预置累加器初值为累加器容量的一半，计算过程示于表3-7。

表3-7 空间直线插补计算过程

按数字积分法直线插补原理，插补直线要给定终点坐标x_e及y_e，这里终点坐标都以绝对值计算，四个象限直线插补方法相同。进给方向的正负由数据处理程序模块直接以标志的形式传递给进给驱动程序，插补程序不做处理。累加器和被积函数寄存器的长度取3～4个字节，一般8位机用3字节，16位机或32位机用4个字节。直线插补程序流程图略。与平面直线相比，空间直线增加了一个积分器，即需要增加一个累加器、一个被积函数寄存器及一个判终计数器。空间直线插补流程略。