数字积分插补法及其应用原理

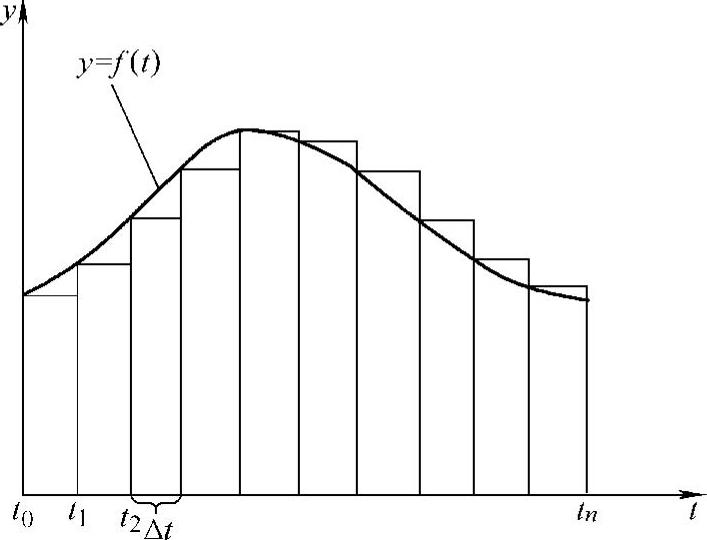
图3-11 函数y=f（t）的积分

数字积分法又称数字微分分析法（DDA），是在数字积分器的基础上建立起来的一种插补法。数字积分法具有运算速度快、脉冲分配均匀、易实现多坐标联动等优点，应用较广泛。下面先介绍数字积分的工作原理，然后再介绍应用数字积分器原理构成的直线和圆弧插补算法。

如图3-11所示，设有一函数，y=f（t），求此函数在t₀～t_n区间的积分，即求函数曲线与横坐标t在区间（t₀，t_n）所围成的面积。此面积可近似地视为曲线下许多小矩形面积之和，即

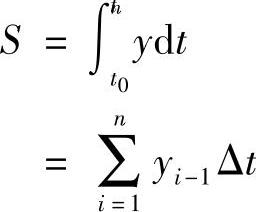
式中y_i为t=t_i时f（t）值。上式表明求积分的过程可以用累加的方式来近似。若Δt取基本单位时间“1”（相当于一个脉冲周期的时间），则上式简化为(www.xing528.com)

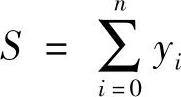
设置一个累加器，而且令累加器的容量为一个单位面积。用此累加器来实现这种累加运算，则累加过程中超过一个单位面积时必然产生溢出，那么，累加过程中所产生的溢出脉冲总数就是要求的面积近似值，或者说是要求的积分近似值。

图3-12是实现这种累加运算的数字积分器框图。它由函数值寄存器、与门、累加器及面积寄存器等部分组成。其工作原理为每来一个Δt脉冲，与门打开一次，将函数值寄存器中的函数值送往累加器相加一次。当累加和超过累加器的容量时，便向面积寄存器发出溢出脉冲。面积寄存器累计此溢出脉冲，累加结束后，面积寄存器的计数就是面积积分近似值。

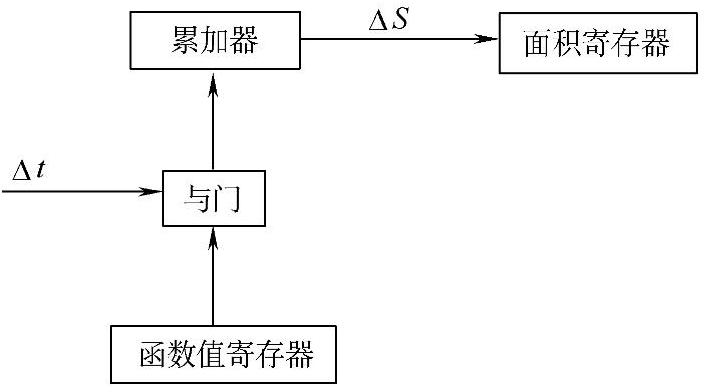
图3-12 数字积分器框图