逐点比较法应用于直线插补

1.直线插补计算原理

（1）偏差计算公式 按逐点比较法的原理，每走一步必须把动点（插值点）的实际位置与给定轨迹的理想位置间的误差以“偏差”形式计算出来，然后根据偏差的正、负决定下一步的走向，以逼近给定轨迹。因此，偏差计算是逐点比较法关键的一步。下面以第一象限平面直线为例来推导偏差计算公式。

假定加工如图3-2所示的直线OA。取直线起点为坐标原点，直线终点坐标A（x_e，y_e）为已知，即直线OA为给定轨迹。m（x_m，y_m）点为加工点（动点）。若m点在直线OA上，则根据相似三角形的关系可得

x_m/y_m=x_e/y_e

即 y_mx_e-x_my_e=0

由此，可定义直线插补的偏差判别式如下：

F_m=y_mx_e-x_my_e （3-1）

若F_m=0，表示动点在OA直线上，如m；

若F_m>0，表示动点在OA直线上方，如m′；

若F_m<0，表示动点在OA直线下方，如m″。

从图3-2上可以看出，第一象限直线插补，当F_m>0时应向+X的方向进给一步以逼近给定直线，而当F_m<0时应向+Y方向走步以逼近给定直线。当F_m=0时，动点在直线上，为了插补能继续进行，不得不从无偏差状态进给一步，走到有偏差状态。这时可以向+X走，也可向+Y走，这里规定为向+X走一步。

于是我们得到第一象限直线的插补法。即当F_m≥0时向+X进给一步，当F_m<0时向+Y方向进给一步。从起点开始，当两个坐标方向走的步数分别等于x_e和y_e时停止插补。

图3-2 第一象限直线

因为插补过程中每走完一步都要算一次新的偏差，如果按式（3-1）计算，要做两次乘法及一次减法，还要算新的坐标值，插补速度很慢，因此算法需要简化。

对于第一象限而言，设加工点正处于m点，当F_m≥0时，表明m点在OA直线上或OA直线上方，应沿+X方向进给一步。因坐标值的单位为脉冲当量，走步后新的坐标值为

x_m+1=x_m+1

y_m+1=y_m

新点的偏差为

F_m+1=y_m+1x_e-x_m+1y_e

=y_mx_e-（x_m+1）y_e

=y_mx_e-x_my_e-y_e

=F_m-y_e （3-2）

若F_m＜0表明m点在OA的下方，应向+Y方向进给一步，走步后新的坐标值为

x_m+1=x_m

y_m+1=y_m+1

新点的偏差为

F_m+1=y_m+1x_e-x_m+1y_e

=（y_m+1）x_e-x_my_e

=y_mx_e-x_my_e+x_e(www.xing528.com)

=F_m+x_e （3-3）

式（3-2）和式（3-3）是简化后的偏差计算公式，公式中只有加减运算，而且不必计算每一点的坐标，只需将前一点的偏差值加上或减去终点坐标x_e，y_e，即可得到新的坐标点的偏差值。由于加工起点是坐标原点，故起点的偏差是已知的，即F_m=0。这样，随着加工点的前进，每一新加工点的偏差F_m+1，都可由前一点的偏差F_m和终点坐标相加或相减得到，非常简单。

（2）终点判别的方法 一种方法是设置∑_x、∑_y两个减法计数器，在加工开始前，在∑_x、∑_y计数器中分别存入终点坐标值x_e，y_e。X或Y坐标方向每进给一步时，就在相应的计数器中减去1，直到两个计数器中的数都减为零时，停止插补，到达终点。

另一种方法是设置一个终点计数器，计数器中存入X和Y两坐标进给的步数总和∑，∑=x_e+y_e，当X或Y坐标进给时均在∑中减1，当减到零时，停止插补，到达终点。

第三种方法是选终点坐标值较大的坐标作为计数坐标。如x_e≥y_e则用x_e做终点计数器初值，仅X轴走步时，计数器才减1，计数器减到零到达终点。如y_e＞x_e，则用Y轴计数。

（3）插补计算过程 插补计算一般用子程序来完成。子程序每运行一次，进给一步，控制子程序运行时间间隔，即可控制进给速度。采用定时中断来控制调用插补子程序时间间隔，控制进给速度。

用逐点比较法进行直线插补计算，每走一步，都需要以下四个步骤：

1）偏差判别。这是逻辑运算，即判别偏差F_m≥0或F_m<0，以确定哪个坐标进给和偏差计算方法。

2）坐标进给。根据直线所在象限及偏差符号，决定沿+X、+Y、-X、-Y四个方向中哪个方向进给，为逻辑运算。

3）偏差计算。进给一步后，计算新的加工点的偏差，作为下次偏差判别的依据，为算术运算。

4）终点判别。进给一步后，终点计数器减1，根据计数器的内容是否为0判别是否达到终点，若计数器为0，表示到达终点，则设置插补结束标志后返回。主程序接到插补结束标志，读下一组新的数据到插补工作区，清插补结束标志，重新开始插补。如终点计数器不为零则直接返回，下一次调用时继续插补。

2.直线插补计算举例

【例3-1】设加工第一象限直线，起点为坐标原点，终点坐标x_e=6，y_e=4，试进行插补计算并画出走步轨迹图。

直线插补计算过程如表3-1所示，表中的终点判别采用了上述的第二种方法，即设置一终点计数器，用来寄存X和Y两个方向的步数和∑，每进给一步∑减1，若∑=0，表示到达终点，停止插补。直线插补走步轨迹如图3-3所示。

图3-3 直线插补走步轨迹

表3-1 直线插补计算过程

3.四个象限的直线插补计算

前面所述的均为第一象限直线的插补方法。第一象限直线插补方法经适当处理后推广到其余象限的直线插补。为适用于四个象限的直线插补，我们在偏差计算时，无论哪个象限直线，都用其坐标的绝对值计算。由此，可得的偏差符号如图3-4所示。当动点位于直线上时偏差F=0，动点不在直线上且偏向Y轴一侧时F>0，偏向X轴一侧时F<0。

由图3-4还可以看到，当F≥0时应沿X轴走步，第一、四象限走+X方向，第三、二象限走-X方向；当F<0时应沿Y轴走一步，第一、二象限走+Y方向，第三、四象限走-Y方向。终点判别也应用终点坐标的绝对值作为计数器初值。

例如，第二象限的直线OA₂，其终点坐标为（-x_e，y_e），在第一象限有一条和它对称于Y轴的直线OA₁，其终点坐标为（x_e，y_e）。当从O点开始出发，按第一象限直线OA₁进行插补时，若把沿X轴正向进给改为沿X轴负向进给，这时实际插补出的就是第二象限的直线OA₂，而其偏差计算公式与第一象限直线的偏差计算公式相同。同理，插补第三象限终点为（-x_e，-y_e）的直线OA₃，它与第一象限终点为（x_e，y_e）的直线OA₁是对称于原点的，所以依然按第一象限直线OA₁插补，只需在进给时将+X进给改为-X进给，+Y进给改为-Y进给即可。

四个象限直线插补的偏差计算公式及进给方向列于表3-2之中。表中L₁、L₂、L₃、L₄分别表示第一、二、三、四象限的直线。

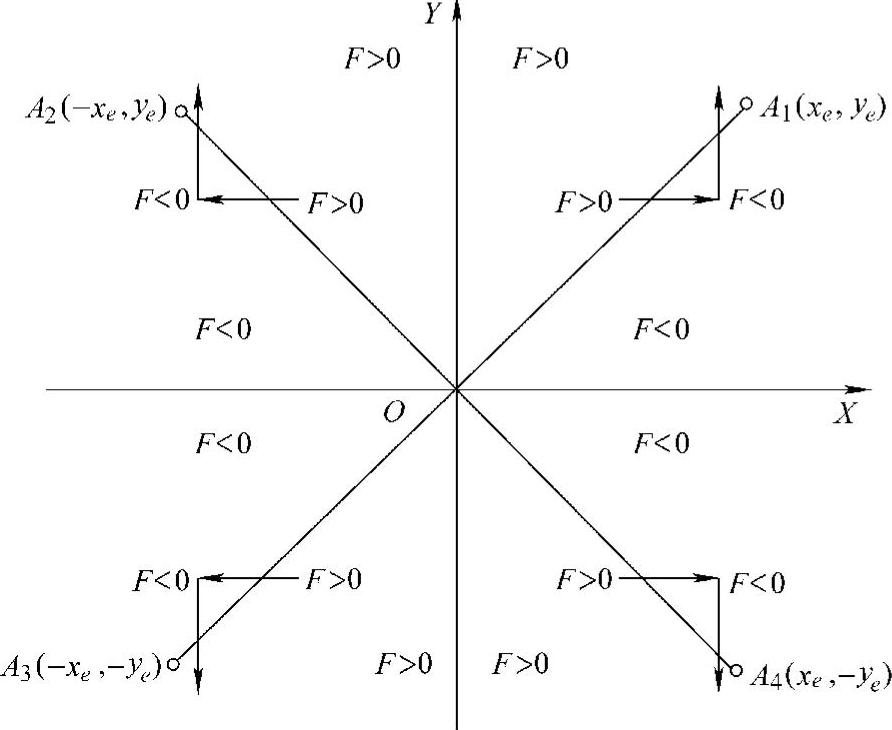
图3-4 四象限直线偏差符号和进给方向

表3-2 直线插补的偏差计算公式及进给方向

4.直线插补计算的程序实现

程序设计首先要明确设计要求，再根据程序要完成的任务划分模块，设计算法及流程图，分配资源，最后进行程序编制。直线插补只是数控系统软件的一个模块，在设计流程图之前，还需确定与其他模块的关系。因为某一象限直线在各轴进给方向是确定的，并且在此直线的插补过程中不变，如L₂为-X或+Y，L₃为-X或-Y。所以，这里插补程序不处理进给方向问题。进给方向由数据处理程序以标志的形式直接传递给进给驱动子程序。开环系统中，进给驱动子程序的功能主要是根据插补结果和进给方向标志，驱动步进电动机运动。直线插补流程图和进给驱动子程序流程图略。