安全阀内部流场形态分析

数值仿真方法相对于传统的试验研究手段最大的优点在于，借助数值仿真方法可以得到整个计算域内各空间点流动参数的近似值，而且CFD软件都同时提供了强大的图形化后处理工具，将计算域内各点流动参数通过云图、等高线、速度矢量图等图形方式展示出来，用户可以很方便地获取流场内部任意一点、任意一条线、任意一个面或任意一个区域内的流动情况，实现流场的“可视化”。本节以一个具体的CFD流场仿真计算结果为例，对安全阀的流场进行详细的描述，该算例的参数如下：规格为2J3；进口压力为1.64MPa，出口压力为大气压；进口温度和出口温度为283K；开启高度为10.68mm；介质为空气。

图5⁃9所示为流场对称截面湍流黏度比云图，从中可以清楚地看出，安全阀内部流场大部分流动区域湍流黏度比很高，最高数值超过60000，说明安全阀内大部分的流动为湍流流动。

图5⁃10和图5⁃11所示分别为安全阀流场对称截面上压力和马赫数云图。从中可以看出介质从安全阀进口到出口的流动过程中，压力和速度的变化。

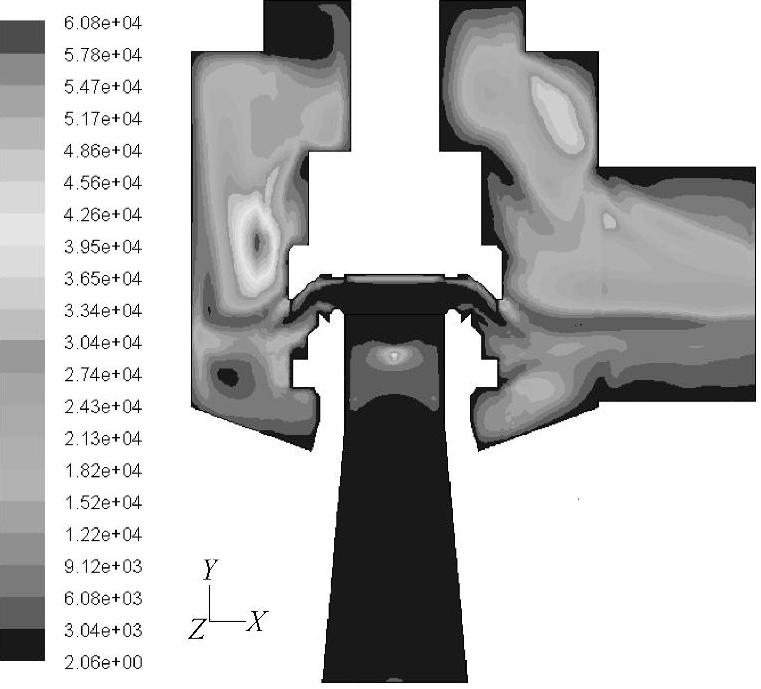
图5⁃9 安全阀流场对称截面湍流黏度比云图

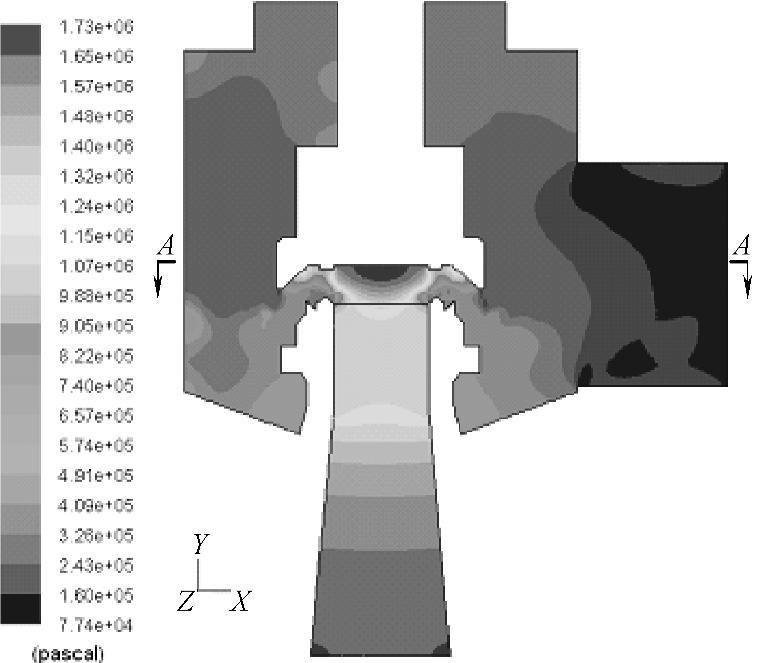
图5⁃10 安全阀流场对称截面压力云图

从阀座进口到反冲盘和调节圈的出口，流道先收缩、后扩张，介质在流动过程中，压力降低、流速增加，其中在阀座出口以后，流动参数变化最为激烈。从图5⁃10中可以看出，在阀座与阀瓣之间形成的圆柱侧面上，流速达到声速流动。流体继续在向下游流动过程中，流道在折转，并在不断扩大，由此产生的激波在固壁和自由边界上反射、相交。介质在其作用下被压缩、膨胀，在下游局部区域形成了一段超声速射流。

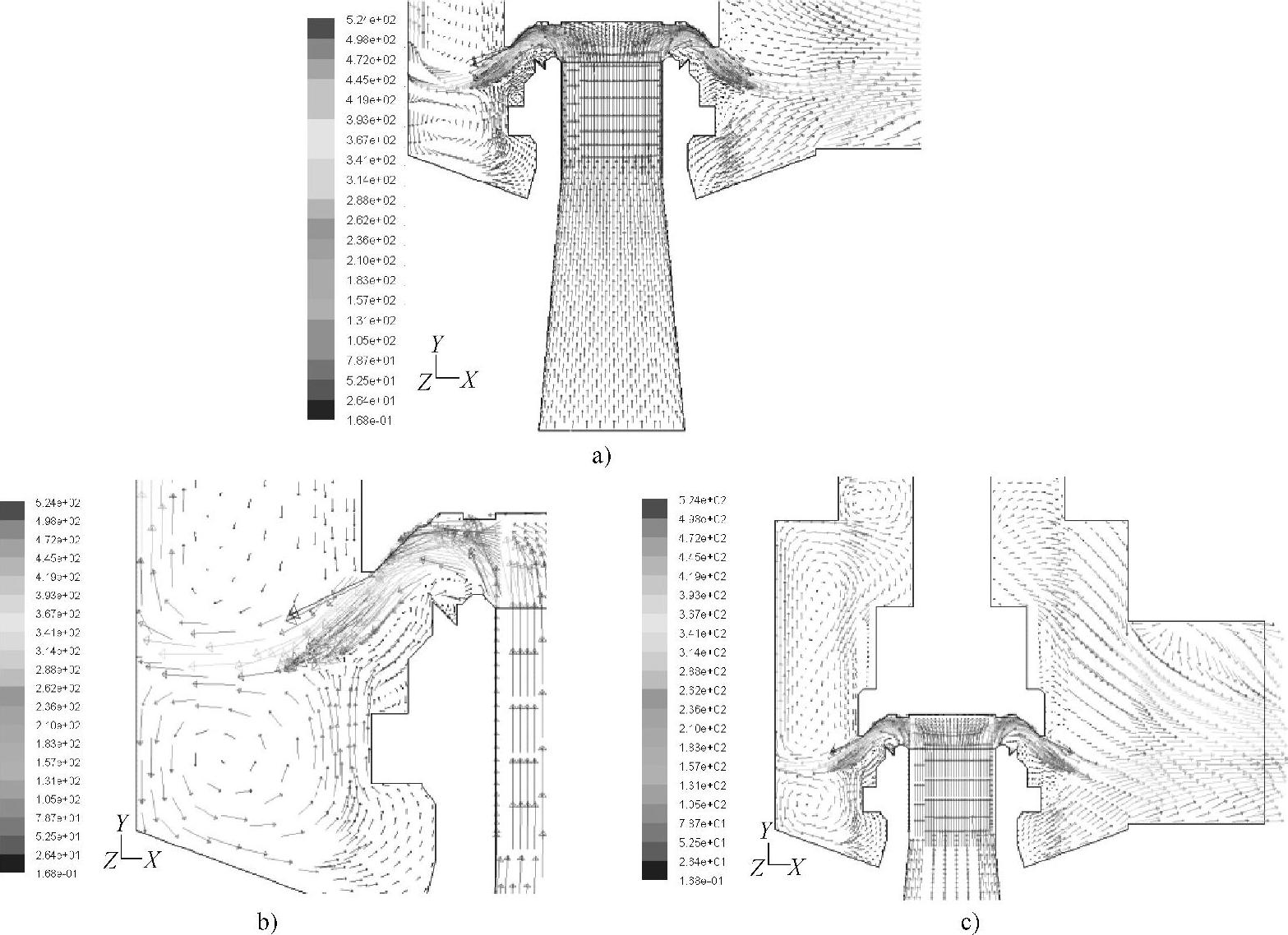
图5⁃12所示为安全阀流场对称截面的速度矢量图，图5⁃13所示分别为阀座内、阀座出口到反冲盘出口流道和阀体内流场速度矢量的局部图。将这些速度矢量图和前面的压力、速度云图相结合，可以更直观地观察和分析介质在流道中的流动情况。

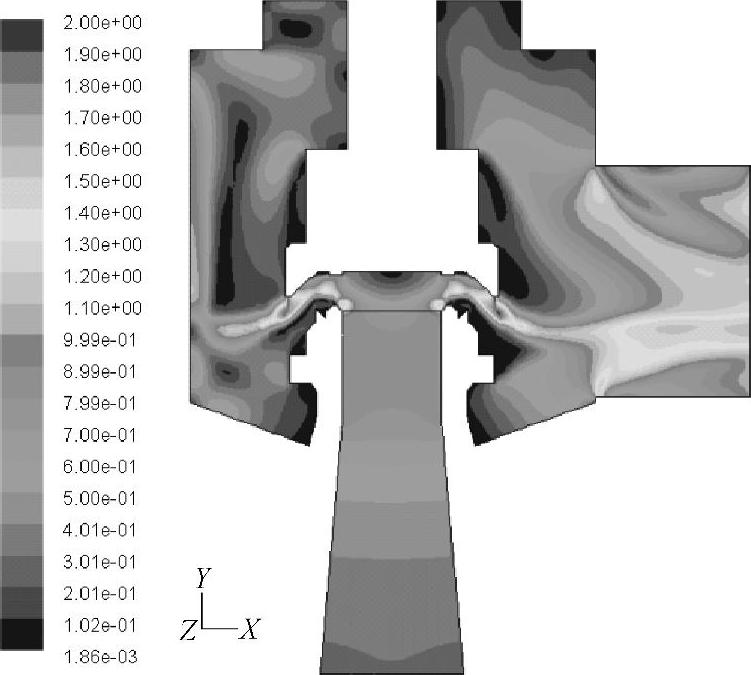
图5⁃11 安全阀流场对称截面马赫数云图

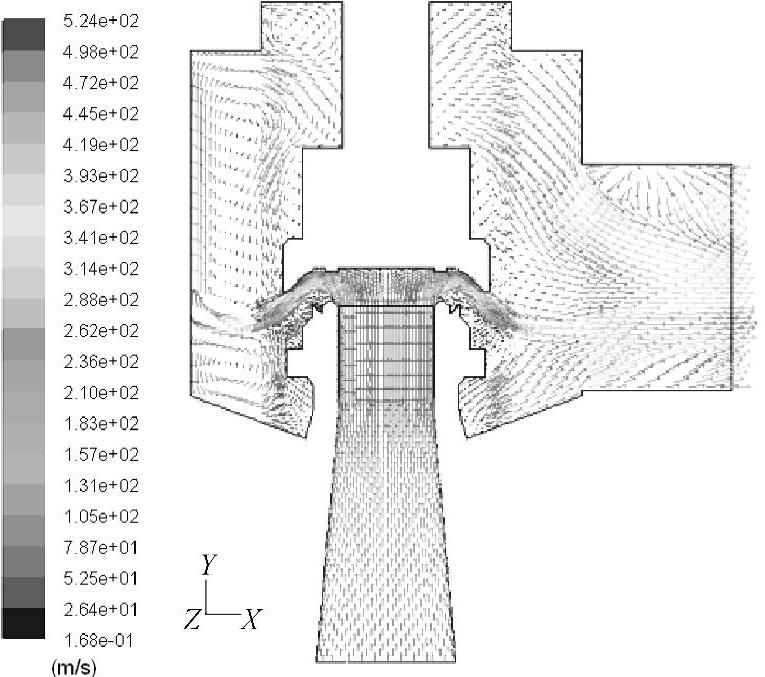
图5⁃12 安全阀流场对称截面速度矢量图（全部）

(www.xing528.com)

图5⁃13 安全阀流场局部区域对称截面速度矢量图

a）阀座内 b）调节圈和反冲盘区域 c）阀体内

如图5⁃13a所示，在阀座内，流道变化平缓，各点介质的流动方向一致。当介质从阀座流出时，与阀瓣底面碰撞，受其阻断，在阀瓣下方形成一个滞止区，正如图5⁃10、图5⁃11和图5⁃13a中所显示的，该区域内，速度很小、静压力增大。

如图5⁃13b所示，介质在流动中遇阀瓣面发生折转，而后遇反冲盘再次发生折转，而且过流截面面积发生突变，因此造成流动异常复杂，各点流动方向变化剧烈，在流道突变处发生流体分离，在阀瓣凸台的下流贴壁面处，以及下调节圈与阀座之间的空间，出现了低速的回流区。

如图5⁃13c所示，超声速射流紧贴反冲盘壁面冲出后遇阀体内壁面又多次折转，最后汇集从阀体出口流出。阀体内产生了很多涡旋、回流区域，这些区域内流速很低，对介质的排放没有多大贡献。

图5⁃14所示为安全阀出口中心线所在的X⁃Z平面（图5⁃10中的A⁃A截面）上的压力云图。图5⁃15所示分别为X⁃Y平面上45°、90°和135°截面的压力云图。

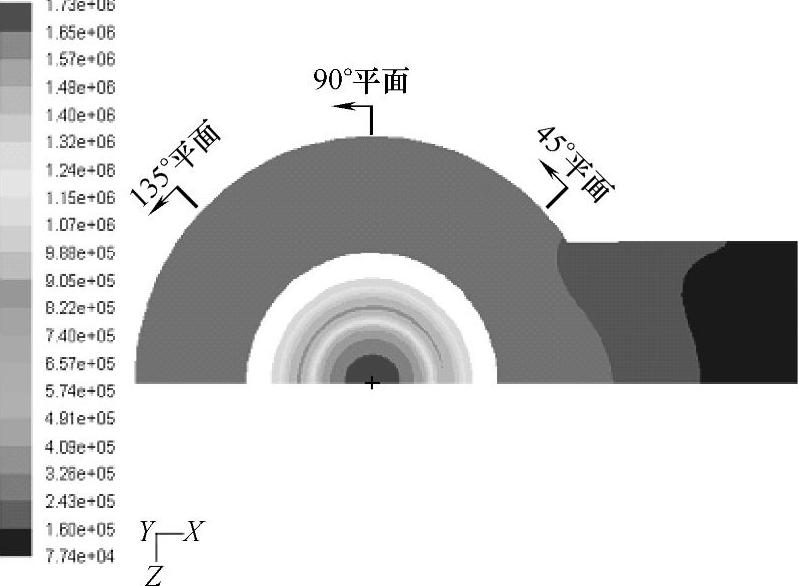
图5⁃14 安全阀出口中心线所在的X⁃Z平面（A⁃A截面）上压力云图

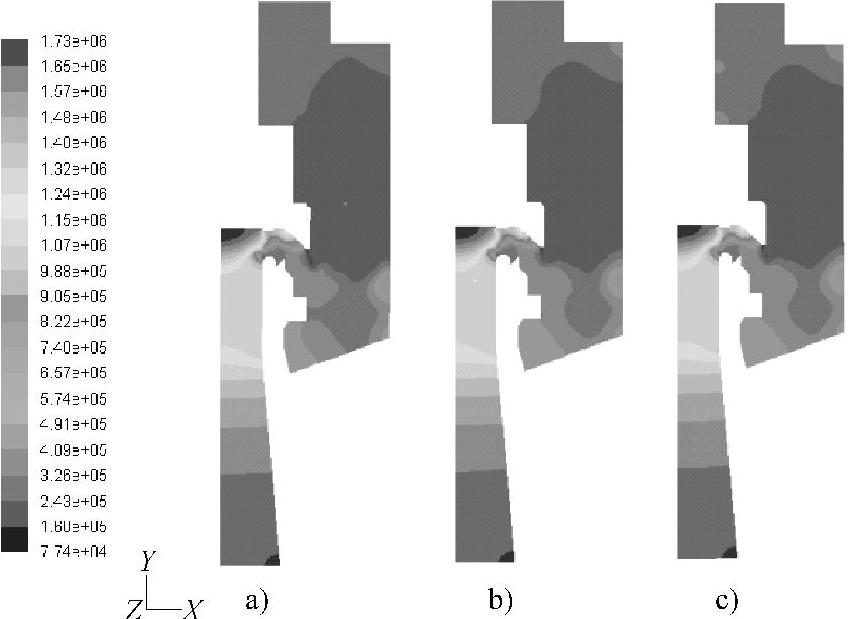
图5⁃15 X⁃Y平面上45°、90°和135°截面的压力云图

a）45°截面 b）90°截面 c）135°截面

从中可以看出，在阀座和阀瓣密封面之间的流道，流动形态是轴对称的，但在阀体内，流动存在一定的差异。

通过对流场形态的可视化观察，对性能特性的物理机理进行透彻的分析。不但知其然，而且知其所以然。CFD的这一优势在本章后面的论述中将得到具体的体现。