冲积河流通过自动调整作用,从较长时期的平均情况看,有可能处于相对平衡状态,在纵剖面和断面形态与流域因素之间应该存在某种定量关系,这种定量关系,一般称为河相关系。河相关系取决于流域来水来沙条件和河床边界条件,这种函数关系可以表达为数学方程式(6.2-1):

式中 B——河槽的水面宽度;
h——河槽的平均水深;
J——河流纵比降;
Q——来自上游的流量及过程;
G——床沙质来量及其过程;
D——河槽的边界条件,包括河床及两岸的物质组成。
可以通过测量资料的统计分析确定上述函数关系。也可以联立求解水流连续方程、水流运动方程、挟沙能力方程和另一个独立方程组成的方程组,得到上述函数关系。有不同学者从能量分配、能耗最小、河床活动性的方面寻找另一个独立方程。
河相关系有两种类型,一种称为沿程河相关系,反映不同河流之间,或者同一河流上下游之间,由于水流、泥沙和边界条件的不同所引起的河床形态的变化。它是通过某一特征流量(往往取造床流量),把不同断面的资料联系在一起,用以描述冲积河床的总轮廓。另一种称为断面河相关系,它研究某个短河段或某个断面在不同流量下断面尺寸和坡降的变化。断面河相能确定断面形态随流量变化的细节。可以用沿程河相关系确定断面的总体轮廓之后,再用断面河相关系确定其变化细节。
河相关系问题的研究已有近百年的历史。河相关系的公式很多,一般是经验公式,适用于特定的流域条件,局限性较大。钱宁通过经验公式分析了河流形态与流域因素之间的关系,得出的主要结论有:流域因素中起作用最大的是流量,河流的纵剖面、断面形态和平面形态无不受流量的影响;来沙量的影响主要反映在河流的比降上;河床物质对比降的影响最大,在其他方面只具次要地位;河岸物质组成主要影响断面的宽深比,河岸抗冲性大时,河流在一定范围内也变得更弯曲一些;河谷比降主要对河流的弯曲系数产生影响。
研究河相关系问题,有助于认识河流形态规律,拟定合理的河道整治方案。工程师们采用时,可以利用本流域的公式或者条件近似河流的经验公式,采用前应进行必要的验证。工程师们一般喜欢简单、直观的公式,用于工程的参考。
6.2.3.1 造床流量
造床流量被作为一个特征流量,认为是其造床作用与多年流量过程的综合造床作用相当的某一种流量。该流量不等于最大洪水流量,因为尽管最大洪水流量的造床作用剧烈,但时间过短,所起的造床作用并不是很大;它也不等于枯水流量,因为尽管枯水流量作用时间甚长,但流量过小,所起的造床作用也不可能很大。因此,造床流量应该是一个较大但又并非最大的洪水流量。造床流量的确定方法有平滩流量法、输沙率法、输沙量法、河床变形强度法、输沙能力法等。造床流量如何选取,至今尚无一致的认识。下面仅列出平滩流量法。
平滩流量是指当大河水位到河漫滩(或边滩的滩边)高度时相应的流量。从试验过程和资料分析均可看出,水位由枯水位上升至平滩水位的过程中,水流的造床作用不断增强,而当水位继续上涨,水流漫滩后,水流分散,造床作用反而有所降低。实际工作中,由于滩地高程不易确切确定,因此一般都是选取一个较长的河段作为依据。
6.2.3.2 河床纵剖面河相关系
河床纵剖面有三种基本类型:下凹型、直线型和上凸型。上凸型剖面极为少见。下凹型剖面很常见,它意味着比降越到下游越平缓,即水流消耗较小的能量也能维持河流的纵向平衡。从不同的尺度看,纵剖面光滑度不同。取较短河段看,纵剖面多呈现锯齿状。从大尺度河段,纵剖面会变得光滑一些。纵剖面形状是地质条件、水沙条件的产物。不同的岩性会造成不同的坡降,河流流经不同的岩性,会造成纵剖面上的折点。河流的侵蚀基面,也会在纵剖面上形成折点。从输沙平衡的角度看,床沙的粗细程度对应不同的坡降,床沙越粗,坡降越陡。在同一流域,流量越大,往往坡降越小。
着眼于全河段河床纵剖面的平均形态,那么它可以被看成一条连续的光滑曲线。根据河流实测资料分析,它大致与枯水期的水面曲线相近。这条几何曲线可以用对数曲线、指数曲线等来描述。
很多学者研究了流量、泥沙、水力因子与河床比降的关系。李保如教授根据长江、黄河、永定河及实验室模型小河的资料,整理而成公式(6.2-2)。钱宁整理黄河资料得到公式(6.2-3)。

式中 Q——平滩流量,m3/s;
S——平滩流量时的含沙量,kg/m3;
d50——床沙中值粒径,mm。
6.2.3.3 横断面河相关系
格鲁什科夫统计天然河流形态的分析成果,得出宽深关系式(6.2-4):

式中 B——河宽,m;
h——平均水深,m;
ζ——河相系数,对砾石河床取1.4,一般沙河取2.75,极易冲刷的细砂河取5.5。
公式(6.2-4)反映了天然河流随着河道尺度或流量的增大,河宽增加远较水深增加为快的一般性规律。我国的资料研究表明(表6.2-1),ζ与河型密切相关,弯曲型河流ζ数值要小,游荡型河流ζ数值较大。
表6.2-1 中国不同河型ζ值变化表(https://www.xing528.com)

阿尔图宁整理中亚细亚河流,提出公式(6.2-5):
![]()
式中 m——变值0.5~1.0,其中平原河流取0.5~0.8,山区河流取0.8~1.0。河相系数ζ根据不同河段位置取值,其中山区河段取10~16;山麓河段取9~10;中游河段取5~9;下游河段壤土河岸取3~4,砂土河岸则取8~10。
维利坎诺夫运用量纲分析法,得到河宽及水深的表达式为式(6.2-6)和式(6.2-7)。
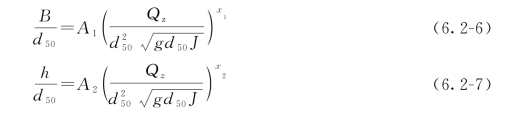
式中 Qz——造床流量;
d50——床沙中值粒径;
J——纵比降;
A1、A2——系数;
x1、x2——指数,根据若干实验室及野外资料求得的有关数据列入表6.2-2。
表6.2-2 式(6.2-6)与式(6.2-7)系数表

6.2.3.4 河湾平面河相关系
冲积河流在流域来水、来沙及河床边界条件制约下,塑造出不同的河湾,不同类型河流的河湾平面形态差别很大。同一类型河流的不同河段,河湾的平面形态差别也较大,研究河湾的平面形态主要研究比较稳定的弯道的形态关系。河湾平面形态的要素如图6.2-5所示。
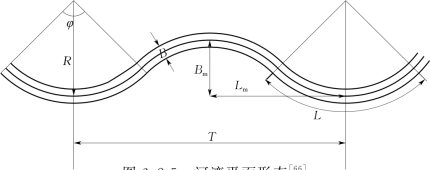
图6.2-5 河湾平面形态[66]
R—弯道中心线的曲率半径;φ—中心角,弯道自进口到出口所包含的中心角;L—弯曲段长度,单个弯曲段的弧线长度;T—河湾跨度,两相邻同向河湾间距;Lm—河湾间距,两相邻反向河湾间距;Bm—弯曲幅度,相邻反向弯道之间的垂直距离;B—直段河宽,两相邻反向河湾间的过渡的直段河宽
河湾形态是不断变化的,同时又具有相对的稳定性;相对稳定的河湾形态出现的概率更大,保持的时间更长。密西西比河179个河湾的统计表明,较多的弯道曲率半径的变化范围为1000~2500m,中心角的变化范围为30°~100°。
河湾形态受流量的影响,它们之间的关系可以表示为式(6.2-8)
![]()
式中,系数K、n的取值见表6.2-3。
表6.2-3 式(6.2-8)中的系数K、n[19,66]

不少学者用直段河宽表示河湾河相关系,如式(6.2-9):

式中 B——直段河宽,m。
系数KR、KT、Km见表6.2-4。
表6.2-4 式(6.2-9)中的系数值[66]

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




