使用层次分析法确定权重的方法

3.4.5.1　层次分析法的优缺点

层次分析法（AHP）是一种系统分析方法，由美国萨迪（T.L.Saaty）教授在20世纪70年代提出，以后得到了快速应用和发展，并衍生出了改进层次分析法、模糊层次分析法、可拓模糊层次分析法和灰色层次分析法等方法。

层次分析法具有诸多优点。它按照分解、比较、判断、综合的思维方式进行决策，可以做到定性分析与定量分析相结合，能够反映决策者对决策问题的认知和判断，并将决策者的思维过程系统化和模型化。它将复杂问题分解为若干层次和若干因素进行分析比较，从而将复杂问题简单化，便于数学计算。它适用于多准则、多目标复杂问题的决策分析，应用范围非常广泛。

层次分析法也有不足。它只能对原有方案排序择优，无法提出新方案。它的过程反映了决策者的判断，但也受制于决策者的主观认识。不同的人对同一问题用层次分析法解决，可能构建各不相同的层次结构模型、判断矩阵，分析得出不同的结论。为克服层次分析法主观判断造成的不足，宜尽量采用对问题理解较深的行业专家的群体判断，明晰决策目标和约束范围。分解问题时要把握主要因素，不要遗漏也不要烦琐化，重要性程度相差太大的因素不能放置在同一层次。

3.4.5.2　层次分析法的步骤

层次分析法解决问题的基本思路是先分解后综合。首先要确定待决策的问题，然后将决策问题分解成不同层次的组成因素，这些因素组成分层隶属关系，形成一个多层分析结构模型，最终分析各层要素相对于上层要素的重要程度，确定权重值，得到各个解决方案的相对优劣次序。

层次分析法的步骤如下：

（1）确定总目标，构建层次结构模型。图3.4-1为一个简单的层次结果模型，共四层。顶层为总目标层，表示要解决的问题。二、三层为基准层，表示考虑的因素和和决策的准则，第四层为方案层，表示决策时的备选方案。

（2）构建判断矩阵，求解特征值和权重向量。

（3）进行层次单排序一致性检验及层次总排序一致性检验。

（4）确定权重向量和方案的优劣次序。

图3.4-1　层次结构模型

3.4.5.3　构造判断矩阵

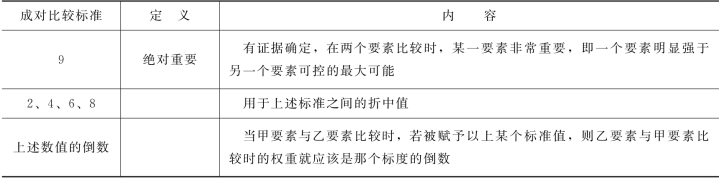
构造判断矩阵时，需要进行各个要素之间的成对比较。萨迪等学者用试验的方法比较了在不同标度下人们判断结果的正确性，认为采用9级比例标尺最为合适（表3.4-4）。

表3.4-4　层次分析法的9级评价尺度[52]

续表(www.xing528.com)

层次结构模型中，元素间的隶属关系可以称为亲要素和子要素。如图3.4-1中，目标S为亲要素，则子要素为A1、A2和A3；A1为亲要素，则子要素为B1、B2、B3；A2为亲要素，则子要素为C1、C2、C3、C4；亲要素A3的子要素则为B4和B5。

根据层次结构模型，对于子要素进行成对比较，可以构造隶属亲要素的各个判断矩阵。在某个亲要素下，记两个子要素的重要性为Ci和Cj，两者之间按表3.4-4规定的评价尺度进行比较，得到Ci∶Cj=aij。例如，Ci相对于Cj为“相当重要”，则aij=5；如果Cj相对于Ci为“相当重要”，则aij=1/5。如果亲元素有n个子元素，则得到n阶判断矩阵A，如式（3.4-13），其中，aii=1，aij与aji互为倒数。

判断矩阵A为正反矩阵，其最大特征向量归一化以后，为子元素的权重。可以采用和积法、方根法、幂法、最小二乘法等近似方法求解判断矩阵的最大特征根和特征向量。下面介绍和积法。

将判断矩阵为A=（aij）n×n中的元素按列归一化，见式（3.4-14）；然后将归一化后的矩阵的同一行的各列元素相加，再除以n得权重向量（wi）1×n，见式（3.4-15）。最大特征根λmax则按式（3.4-16）计算。

3.4.5.4　一致性检验

判断矩阵的要素之间要满足一致性要求。按照逻辑关系，如果元素甲比元素乙重要，元素乙比元素丙重要，则正常的判断应为元素甲比元素丙重要，否则会出现逻辑判断的混乱和不一致。如果判断矩阵A为基本一致性矩阵，那么会满足式（3.4-17）。但由于实际工作的复杂性，决策者很难对aij精确取值，aij取值会与式（3.4-17）的要求存在一定的偏差，这种偏差只要控制在一定范围，就不会影响判断结果的合理性，因此需要进行基本一致性检验。

按式（3.4-18）设立判断矩阵的一致性指标CI。CI越大，判断矩阵的不一致性越严重。再按式（3.4-19）引入一致性评价指标CR和随机一致性指标RI。RI按表3.4-5取值。当CR=0时，称判断矩阵是完全一致性矩阵，CR＜0.1时，认为判断矩阵是满意一致性矩阵，当CR＞0.1时，称判断矩阵不具有一致性。

表3.4-5　随机一致性指标RI

对于单个判断矩阵进行的一致性判断为单排序一致性检验。对于底层和目标层之间的一致性，要进行层次总排序一致性检验，检验标准也为CR＜0.1，其中CR按式（3.4-20）计算。式（3.4-20）中CIj、RIj为与wj对应的该层次中判断矩阵的一致性指标和随机一致性指标。

当单排序一致性检验和总排序一致性检验均满足CR＜0.1时，认为判断矩阵的一致性可以满意，由其计算出来的权重可以接受。当一致性检验CR≥0.1时，应对判定矩阵进行基本一致性修正，修正的方法可以参考层次分析法的有关文献。