加锚节理岩体的三维重构方法优化

为了实现对加锚节理试件不同断层的裂隙演化规律的研究,利用前文的图像处理技术分析了加锚节理试件的不同扫描断层的CT扫描图像,但是由于分析研究断层的角度始终在二维阶段,导致其结果具有很大的局限性。计算机的功能随着计算机的飞速发展逐渐变得丰富全面,利用计算机技术已经可以对加锚节理试件展开三维研究,为了更加准确地分析加锚节理试件破坏前和破坏后的两种状态,将CT扫描得来的图像导入Mimics软件中,进行三维重构。

1)试件内部破裂的分形描述

为了实现定量分析岩体内部破裂情况,进而对剪切蠕变作用下加锚节理试件的内部破裂状态进行描述,所以本节基于本章前文中的图像处理以及三维重构的基础上引入分形理论来进行分析。借助盒维数进行分形描述,盒维数计算示意图如图5.37所示。

图5.37　盒维数计算示意图

(1)盒维数定义

首先选择边长为r的小盒子,把需要研究的图像覆盖住,然后统计含有裂隙的非空盒子数目[记为N(r)];盒子的个数随着边长r的减小,而逐渐增大,当r→0时,便可得出所求的分形维数。

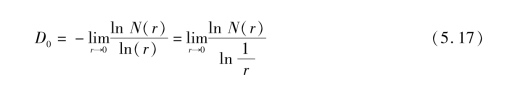
当实际计算时,r不是无限的,需要选取一系列r和N(r),然后借助最小二乘法在双对数坐标中拟合得到直线,表征其分形维数的是直线的斜率。

盒子的边长一般取:

式中　r0——盒子的最小边长。

(2)差分盒维数

引入差分盒维数是因为利用盒维数进行计算会产生较大的误差,导致不能充分利用CT图像中的有效信息。因此,可将差分盒维数法看成盒维数法基础上的进一步完善,分形计算给定面积为M×M的CT二值化图像。为了覆盖要分形的图像,将该图形分割成为s×s个小块,可以选择边长为r的盒子,s是一个整数,1≤s≤M/2记为r=s/M。可将面积为M×M的图像模拟成一个三维空间,(x,y)表示某个像素点的平面位置,用像素点的灰度值表示第三维度的坐标。通过上述处理就能把CT图像划分成多个s×s的网格,可以理解为在任意的一个网格位置上存在一系列体积为s×s×s的盒子。假设在图像的第(i,j)个网格中,在第1个小盒子中存在最大的灰度值,在第k个小盒子中有最小的灰度值,则Nr在第(i,j)个网格内的分布nr(i,j)为:

对所有的格子nr(i,j)求和,则有Nr=∑nr(i,j)。

每一个不同的s,都有一个r与之对应的,经过r随s的不断变化而变化的多次变换,能获得一系列的r～N(r)的散点图,通过这些散点可以拟合出ln N(r)-ln(1/r)曲线,分形维数D即为该直线的斜率。

(3)利用Matlab计算分形维数

借助Matlab软件能够更利于对分形维数进行计算分析。具体步骤如下:

①读取图像。将图片转化成计算机能够辨识的信息,具体方法是用imread函数对图片中的信息进行处理,记录图片信息是通过数据字节形式进行的,除此之外,还有一部分数据信息以二维数组的形式对应图片中的每个像素点的信息。

②处理原始图像得到灰度图像。利用Matlab软件通过rgb2gray(I)函数,对原始图像进行灰度处理。(www.xing528.com)

③处理图像边缘。通过edge(I)函数,对图像边缘进行检测,从而分割出截面的边界,以免截面附近的空气影响分形维数的分析。

④确定图像尺寸。通过size(I)函数,调出图像矩阵的行数和列数,进而确定图像的尺寸。

⑤求出Nr等数据。选择尺寸为M×M的CT图像,盒子的尺寸选取s(1≤s≤M/2,s=2,4,8,…),计算尺度r=s/M将CT图像划分为s×s×s的盒子,计算每个盒子的nr(i,j)值,则M×M区域内对应尺度r下的盒子数为

⑥曲线拟合。通过Polyfit函数进行曲线拟合,得到分数维数D。

(4)结果分析

将得到的分形维数信息放置在表5.10中,以节理倾角为0°的加锚节理试件为例,作图5.38。

图5.38　0°节理倾角的加锚节理试件分形维数曲线

根据盒维数的定义,完整岩体的分形维数是3。随着剪切蠕变作用下锚固节理试件内部破裂程度的增加,分形维数逐渐变小。

2)含不同角度的节理加锚试件的三维重构模型研究

对CT扫描得到的原始图像进行处理,利用Mimics将经过处理后的CT图像进行三维重构,对经过三维重构后的图像进行分析,得到表5.10。

表5.10　不同节理倾角的加锚节理试件内部破裂情况的参数统计

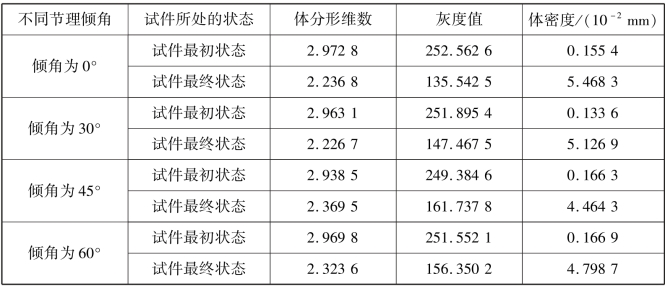
注:t是体密度,即裂隙的面积与试件体积之比。

结合表5.10和图5.28可以得到图5.39,由图分析可知,体密度随着节理倾角的增加开始减小,到倾角为45°时最小,然后增大,说明节理倾角的变化影响着在长期剪切荷载作用下的加锚节理试件其内部的破坏情况。随着节理倾角的改变,体分形维数和灰度值也发生了变化,说明这两种也可以作为判断加锚节理试件的破坏程度的指标,从而对剪切蠕变作用下加锚节理试件的细观规律加以分析。

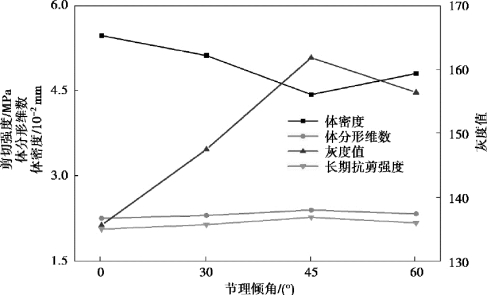
图5.39　长期抗剪强度与各细观参数随节理倾角变化曲线

在图5.39的基础上作进一步分析,得到图5.40。通过图5.40(a)可以看出,长期抗剪强度与体分形维数之间有着较强的相关性。由图5.40(b)和图5.40(c)可以得到与图5.40(a)类似的结论,即长期抗剪强度与体分形维数、体密度、灰度值之间存在较为理想的相关性。由分析可知,节理试件的长期抗剪强度随灰度值、体分形维数的增大而增加,而随体密度的增大而减小。以上研究表明,通过体分形维数、体密度、灰度值等相关参数对加锚节理试件的裂隙发展规律进行描述,从而确定加锚节理试件的长期抗剪强度是可行的。

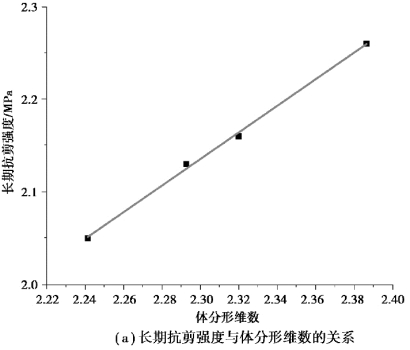
图5.40　长期抗剪强度与体分形维数、灰度值、体密度的关系曲线