参数识别方法及应用于GTN模型中的力学参数求解

GTN模型中需要确定9个参数,可将其分为以下3类[77]:

①q1,q2,q3为孔隙间相互作用参数,对于金属材料来说,考虑孔隙周围非均匀应力场和相邻孔隙之间的相互作用,取q1=1.5,q2=1.0,q3=2.25。

②f0,sn,εn和fn是材料孔隙体积分数参数,其中,f0是初始孔隙体积分数;sn为表征孔隙体积分数的离散程度,一般取0.1;εn为塑性应变水平,一般取0.3;fn为控制损伤的演化率。

③fc和fF为韧性断裂参数,其中,fc为控制累计孔隙体积分数的增长,fF为控制材料的断裂,其中部分已知参数见表5.3。

表5.3　GTN模型适用参数

1)GTN屈服函数参数识别

(1)静水应力p

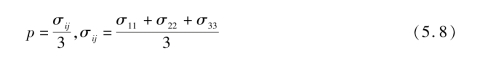
式中　σij——材料应力,代入得p为0.1 MPa。

(2)von Mises等效应力q

式中　sij——柯西应力的偏应力分量,Pa;

δij——克罗内克记号,代入上式得等效应力为10.5 MPa。

(3)基体材料的屈服应力σm

为求解GTN模型参数,取法向应力0.3 MPa作用下,剪切应力为18.3 MPa时的剪切蠕变试验结果绘制,如图5.10所示,等效应力采用Swift[82]强化模型对剪切试验曲线初期阶段进行拟合求解,其计算式为

式中　k,ε0——材料参数;

n——硬化指数。

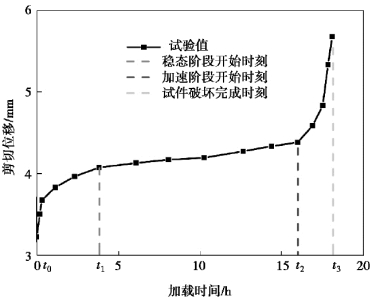
图5.10　剪切蠕变曲线

通过对图5.10中(t0-t1)时刻剪切蠕变曲线初期阶段进行拟合,拟合得到k=52.79,ε0=0.198,n=0.36,将参数代入式(5.10)得

取t1时刻的应变代入式(5.11)得到基体材料的屈服应力为0.229 MPa。

2)孔隙体积分数求解

孔隙体积分数表示均质或非均质材料内部微孔隙的体积占材料总体积的百分比,是一种外力加载下材料损伤的具体形式。以求解fF为例,说明不同孔隙体积分数的求解步骤:

①确定各孔隙体积分数对应的试件的剪切蠕变状态,如fF试件在加速阶段开始时的孔隙体积分数。

②对确定好蠕变状态的试件进行CT扫描,每个图层间隔为100μm,塑性剪切破碎带约为2 cm,共有扫描图层200个。

③利用Matlab图像处理软件对CT图进行二值化处理,通过调节阈值,找到节理剪切破碎带不同位置的清晰图像,如图5.11所示。

图5.11　Matlab处理图(www.xing528.com)

④将处理后的图像导入三维重构软件,基于商业三维重构软件Mimics和开源软件Image J对图片中的裂隙进行了标记、分割和三维特征参数的测量,图5.12为试件塑性剪切破碎带的三维重构图,其中,黄色部分为裂隙或孔隙,绿色部分为试件,通过测算得到的孔隙体积分数,可作为宏观破坏时的孔隙体积分数fF。

通过上述步骤对试件的不同阶段进行处理,利用对时间因数M的不同取值,得到不同孔隙体积分数,见表5.4。

图5.12　三维Mimics重构图

表5.4　不同孔隙体积分数

3)试验参数识别

(1)元件参数求解

利用试件剪切蠕变破坏阶段的应变-时间曲线,根据以下步骤可求得式(5.7)中的相关元件参数,见表5.5。

①确定EB,由式[5.7(a)]可知,当t=0时,ε(0)=σ(0)/EB,而σ(0)=0.3 MPa,ε(0)可由试件剪切流变试验曲线得到,可得EB=σ(0)/ε(0)。

②确定σs,由图[5.7(c)]可知,0.3 MPa法向应力下对应的试件剪切蠕变的长期强度为18.1 MPa。

模型试验参数识别,见表5.5。

表5.5　模型试验参数识别

(2)有效孔隙体积分数的系数求解

由于加速段为非线性变化,且幂指函数的自身特点也更加符合加速蠕变的规律,所以令

将式(5.12)代入式[5.7(c)]中,得

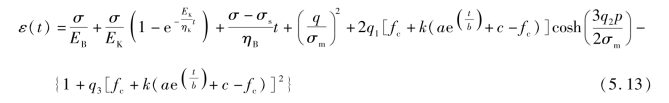
将表5.5中的系数代入式(5.13),利用数学优化软件1stOpt,基于准牛顿法和通用全局优化法对图5.10中t2-t3时间段的试验值进行参数识别,可求EK,ηB,ηK的值见表5.5,得到有效孔隙体积分数的相关系数见表5.6。

表5.6　有效孔隙体积分数的系数

4)拟合结果分析

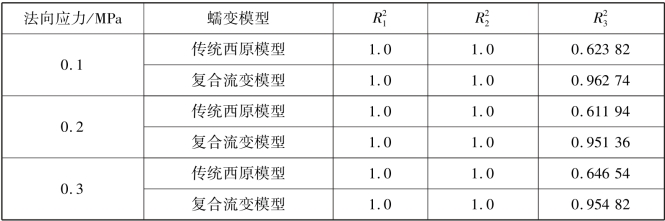
利用传统西原模型和复合流变模型分别拟合不同法向应力下试件剪切蠕变过程曲线,结果如图5.13所示,并对两种模型不同时刻曲线的拟合系数进行对比,见表5.7。

图5.13　蠕变模型数值拟合结果与试验结果对比

表5.7　模型不同阶段拟合系数表

由图5.13可知,传统西原模型与复合流变模型均能够较好地描述试件剪切流变的衰减、稳态阶段,但在试件加速流变阶段,传统西原体模型依然近似保持稳态阶段的剪切速率不变,而实际情况是剪切速率呈现指数增长,与实际不符,而复合流变模型在加速蠕变阶段则能够较好地匹配其剪切速率。为了更加准确地分析两种模型,制作其在不同法向应力下各阶段的拟合系数表,见表5.7,其中表示衰减阶段拟合系数、表示稳态阶段拟合系数、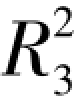表示加速阶段拟合系数,从表中可知,两种模型和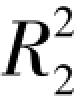都相等且为1,这说明两种模型均能够较好地描述衰减与稳态阶段;不同法向应力下复合流变模型的均在0.95以上,而传统西原模型的平均值仅为对应阶段复合流变模型的64%,这说明相较于传统西原模型,复合流变模型能够更加准确地描述试件在加速阶段的各个状态。