剪切蠕变特性的分析与研究

1)长期强度

为求解试件的长期强度,通过对图5.3采用Boltzmann叠加原理,以每级相同时间间隔为参数,绘制不同法向应力下剪切应力-位移的等时曲线簇,其中,0 d为每级剪切应力施加时的相对起始时间,如图5.6所示。

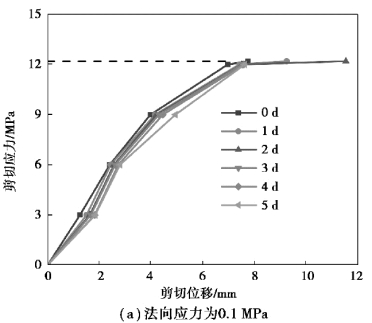
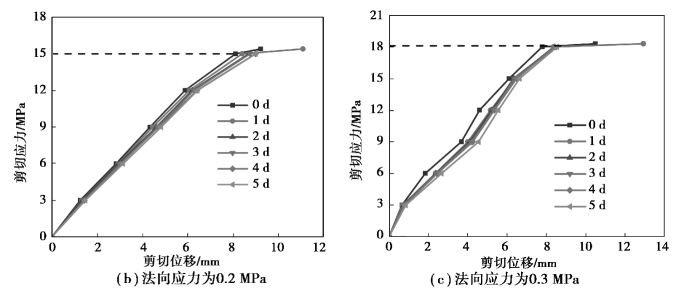
图5.6　剪切蠕变等时簇曲线

由图5.6可知,不同法向应力下试件的长期强度不同,当法向应力分别为0.1,0.2,0.3 MPa时,其长期强度分别为12.2,15,18.1 MPa,曲线在长期强度之前近似为线性变化,随着剪切应力的增加,剪切位移逐渐变大,试件节理经历了由闭合到扩展的过程;而当剪切应力大于长期强度后,曲线近似呈现水平状态,其原因是随着剪切应力水平的增大,试件抵抗变形的能力降低,当超过剪切强度时,试件已经发生破坏,试件失去抵抗剪切的能力,从而出现当剪切应力恒定时,剪切位移随时间而变化的现象。

2)剪切速率

为了更好地研究剪切蠕变全程,以0.1 MPa法向应力为例,绘制剪切速率随时间变化的曲线,如图5.7所示,由图可知,不同剪切速率随着时间呈现先急剧下降而后逐渐接近于某一定值的趋势,当时间一定时,随着剪应力水平的提高,蠕变速率增加,由分析可知,蠕变速率描述的是单位时间内的蠕变量,剪应力越大,在相同法向应力下的剪切位移就越大;在衰减蠕变阶段,蠕变速率随着时间呈现断崖式下降,其原因在于,在剪切蠕变初期,由于试件具有抵抗剪切破坏的能力,使得剪切速率大幅度下降;在稳态或亚稳态蠕变阶段,蠕变速率曲线下降速度减慢,逐渐趋向于0,在此阶段,节理逐渐发育、扩展,由于试件抵抗剪切破坏的能力逐渐下降,使试件中节理的发育速度降低,直至为0;在加速蠕变阶段,试件发生新生节理的贯通,蠕变速率上升,曲线近似呈现“U”形。(www.xing528.com)

3)剪切模量

为了定量描述剪切模量随着时间的变化,以法向应力0.3 MPa为例,取各相对时刻下不同剪应力水平和与之对应的应变来进行线性回归,拟合出直线的斜率即为对应的剪切模量,整理出各时刻对应的剪切模量绘制拟合曲线如图5.8所示。

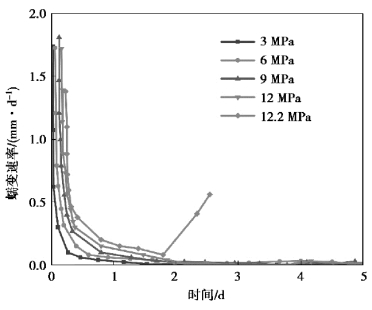
图5.7　蠕变速率-时间曲线

图5.8　剪切模量-时间关系曲线

由图5.8可知,剪切模量随着时间的推移逐渐变小,且减小的速率也越来越小,逐渐趋于恒定,采用对数函数对其进行拟合,其拟合系数R2为0.981 86,说明拟合效果较好,能够用对数函数描述剪切模量随时间的变化关系。