【摘要】:无节理加锚试件蠕变变形与锚杆预应力损失耦合效应模型参数,见表4.6。理论推导值较为接近预应力损失试验结果,可以较好地反映单轴压缩蠕变变形导致的锚杆预应力损失规律。图4.37节理试件锚固区回弹变形曲线图4.38不同倾角节理试件锚杆预应力损失对比曲线
无节理加锚试件蠕变变形与锚杆预应力损失耦合效应模型参数,见表4.6。
表4.6 无节理加锚试件蠕变变形与锚杆预应力损失耦合效应模型参数

通过式(4.11)计算出锚固区范围弹模损失值,根据预应力锚杆在预应力损失阶段由于横向应力导致端头的回弹变形,利用公式σ=E′s·ε,计算预应力损失值,具体结果分析如图4.36所示。

图4.36 节理试件锚杆弹模损失曲线(https://www.xing528.com)
由图4.37可知,锚端回弹变形趋于非线性变化。随着倾角减小,回弹曲线降低速率先增加后减小,回弹变形时间由1.5 min递减为0.5 min,相比无节理试件,其回弹变形时间明显减小,说明节理存在加速了预应力的损失速率。
经预应力损失计算公式得到锚杆预应力损失规律,由图4.38可知,由于施加预应力较小,导致纵向蠕变应力的横向应力分量远大于预应力值,预应力损失时间段多发生在起始阶段,随着应力水平的增加,预应力损失曲线呈非线性递减。3种倾角节理试件的锚杆预应力损失时间分别为1.5,0.5,1 min。理论推导值较为接近预应力损失试验结果,可以较好地反映单轴压缩蠕变变形导致的锚杆预应力损失规律。

图4.37 节理试件锚固区回弹变形曲线
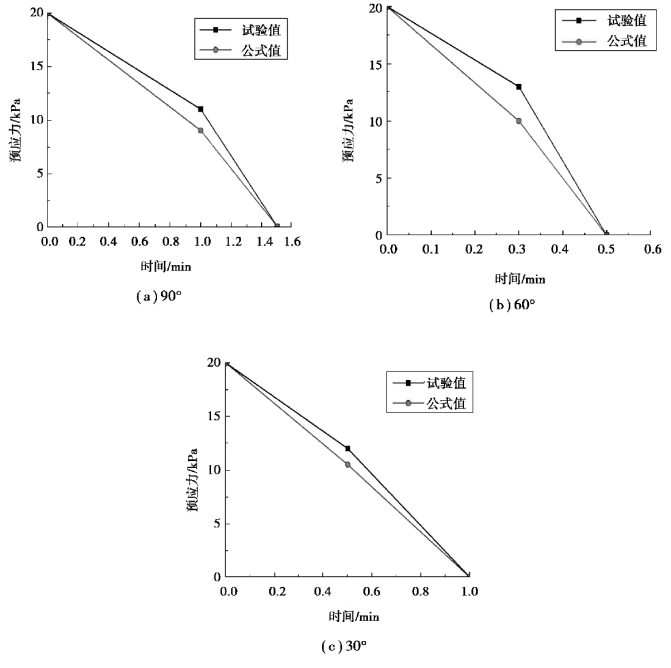
图4.38 不同倾角节理试件锚杆预应力损失对比曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




