加锚节理岩体蠕变变形与锚杆预应力损失的耦合效应分析

1)加锚节理岩体蠕变变形与锚杆预应力损失耦合效应模型的建立

大量工程实例表明:岩体工程失稳破坏与其内部节理、裂隙发育、扩展、贯通息息相关。有必要针对节理加锚试件蠕变变形与锚杆预应力损失耦合效应进行研究。本节以单条节理加锚试件为分析对象,设置3种节理倾角,分析不同节理角度的岩体蠕变变形特征与锚杆预应力损失耦合效应。参考Chen等[69-70]在Sharma和Pande的流变模型[71]的基础上提出了新的加锚节理岩体流变模型构建方式,将整体模型分为岩体部分与节理部分,两部分均采用广义开尔文模型并将其串联,表征模型整体蠕变分为密实岩体变形与节理变形之和,模型如图4.19所示。

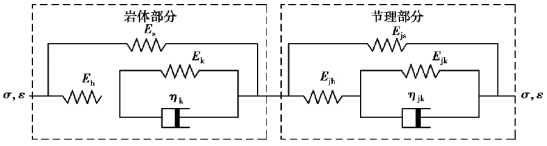
图4.19　加锚节理岩体蠕变变形与锚杆预应力损失耦合效应模型

已知式(4.8)为

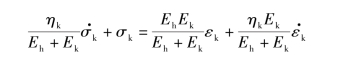
式中　Eh,Ek,ηk——岩体的元件参数。

节理部分本构方程为

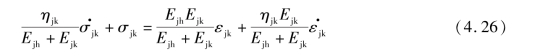
式中　Ejh,Ejk,ηjk——节理的元件参数。

对于均质岩体,假设锚杆自由段预应力均匀分布在均匀岩体上,那么锚杆体的弹性模量可以等效转化为式(4.9)、式(4.27)。

式中　E1——锚杆实际弹性模量,Pa;

As——锚杆体侧向截面面积,cm2;

Ar——锚杆体侧向有效锚固范围内岩体截面面积,cm2。

设定锚杆弹性模量随时间变化的损失函数y=at+b,用来表征轴向压力对侧向锚杆预应力的损失程度。则E′s=Es(at+b),当t=0时,E′s=Es,则b=1,E′s=Es(a′t+1);则E′js=Ejs(a′t+b);当t=0时,E′s=Ejs,则b=1,E′s=Ejs(a′t+1)。

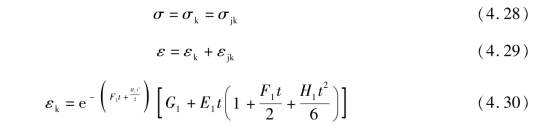
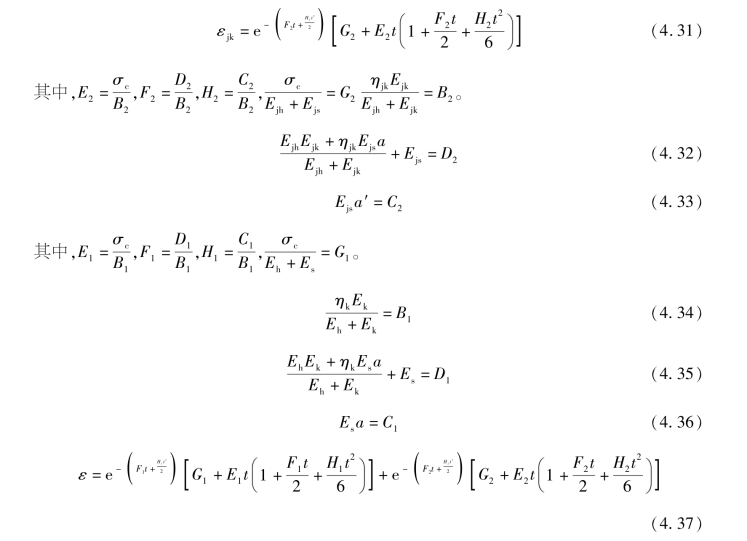
2)加锚节理岩体蠕变变形与锚杆预应力损失耦合效应数值试验

(1)计算假定

本节采用有限元软件FLAC3D进行数值模拟。根据实际情况,采用了以下假定:

模型试件为均质、连续、各向同性体,节理部分采用实体加接触面结构,节理长15 cm,宽5 cm,厚5 mm。节理与锚杆夹角设置3种角度,分别为30°,60°,90°。

(2)试验模型

模型锚杆采用pile结构单元建立,视为弹性体材料,不考虑预应力锚杆自身的应力松弛。蠕变运算采用数值软件内置Viscous经典蠕变本构模型对锚固系统进行粘-弹特性分析。

取边长15 cm的正方体模型视为试件模型,锚杆直径10 mm,锚杆长15 cm,预应力施加值20 kPa,模型具体参数同前文。不同角度节理数值模型如图4.20所示,数值实验材料参数见表4.5。

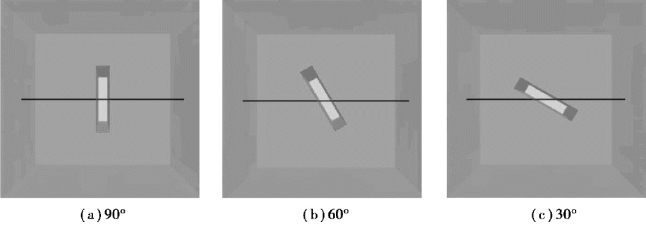
图4.20　不同倾角数值试验模型

表4.5　数值实验材料参数

3)数值试验结果分析

(1)90°倾角节理试件蠕变规律

如图4.21所示,取90°节理试件1,4,7,10 h x-z平面纵向蠕变云图分析,由x-z平面纵向蠕变变形趋势可以观察到,由于预应力锚杆的锚固效果,在施加荷载初始阶段,试件产生了不均匀变形,致使试件局部变形量较大。由于节理弱面存在,相同水平位置,节理轴向变形较大。随着蠕变荷载施加的时间增加,试件轴向平均蠕变量减少,并趋于均匀。说明随着蠕变变形过程,预应力锚杆的锚固效果呈减弱趋势。节理面的存在,使试件整体变形呈两边向中心递减趋势增加,且节理面增加了与其变形值相同的变形范围。

图4.22是以试件顶面中心单元为例的纵向蠕变曲线,由图可知,随着轴向荷载的施加,试件产生了0.61 mm的瞬时变形量。试件的初始蠕变阶段发生在0～2 h内,其间试件纵向蠕变速率随时间增加逐渐降低,蠕变曲线主体呈下凹形,当t=2 h时,试件纵向蠕变速率达到最小值。试件的等速蠕变阶段发生在2～10 h内,蠕变量随着时间缓慢递增并最终趋于稳定。蠕变曲线近似直线,最终蠕变量为0.866 mm。

图4.23为试件在轴向压缩蠕变过程中,取1,4,7,10 h x-z平面横向的蠕变变形云图。由图可知,试件由于预应力锚杆作用,试件首先发生了明显的剪切变形特征,呈倾斜不均匀变化,由于竖直方向节理面的存在,使得试件在横向蠕变变形量增大,随着蠕变时间增加,预应力锚固效果减弱,试件切向蠕变变形沿节理趋于均匀分布,最终产生劈裂变形趋势,出现了扩容现象。相比无节理模型,横向最终蠕变变形量增加。

图4.21　90°节理试件x-z平面纵向变化规律

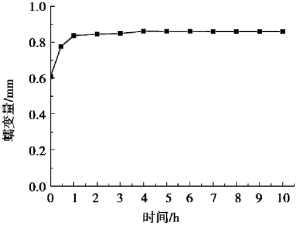
图4.22　90°节理试件纵向蠕变曲线

图4.24为x=0时断面中心点横向蠕变曲线。由图可知,随着轴向荷载的施加,试件横向并未随即产生瞬时变形。待锚杆预应力值损失至0,t=1.5 min后,试件产生了0.078 mm的瞬时变形量。试件的初始蠕变阶段发生在0～2 h内,其间试件横向蠕变速率随时间增加而降低,蠕变曲线主体呈下凹形,当t=2 h时,试件纵向蠕变速率达到最小值。试件的等速蠕变阶段发生在2～10 h内,蠕变量在2～5 h内产生较明显的等速蠕变现象,在5 h后,试件横向蠕变量趋于稳定。最终蠕变量为0.14 mm。相比无节理试件,其初始变形及最终变形值均增加,进入等速蠕变阶段时间减小。(www.xing528.com)

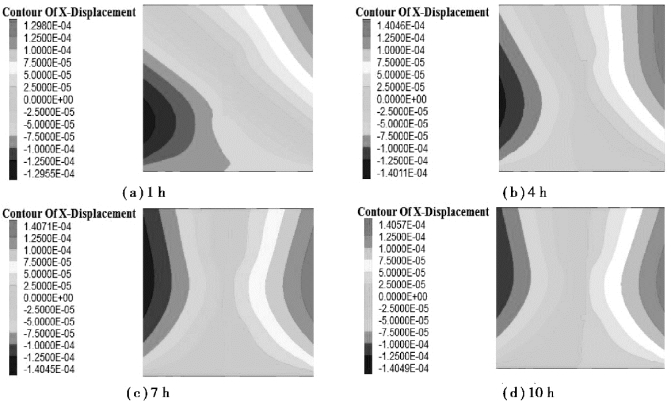
图4.23　90°节理试件x-z平面横向变化规律

如图4.25所示,由于倾角为90°的节理弱面的存在,试件最终的变形趋势沿节理中心发生劈裂变形。

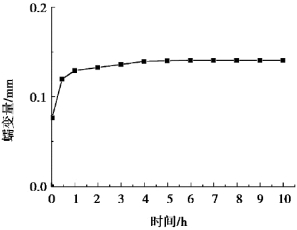
图4.24　90°节理试件横向蠕变曲线

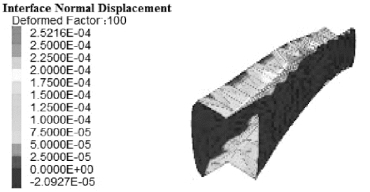
图4.25　90°节理试件接触面变形

(2)60°倾角节理试件蠕变规律

如图4.26所示,取1,4,7,10 h x-z平面纵向蠕变云图分析,由x-z平面轴向蠕变变形趋势可以看出,由于预应力锚杆的锚固效果,在试件施加荷载初始阶段,试件产生了剪切变形,试件右侧局部变形量较大。由于节理弱面存在,相同水平位置的节理轴向变形较大。随着蠕变荷载的完全施加,试件轴向平均蠕变量少量减少,并趋于均匀。说明随着蠕变变形过程,预应力锚杆的锚固效果呈减弱趋势。节理面的存在,使试件整体变形呈两边向中心递增趋势,并且节理面增加了变形范围。相比90°试件轴向变形规律,其轴向蠕变量数值增加,形成的剪切趋势增加,并在蠕变应力作用下,最终形成V字区范围的增加。

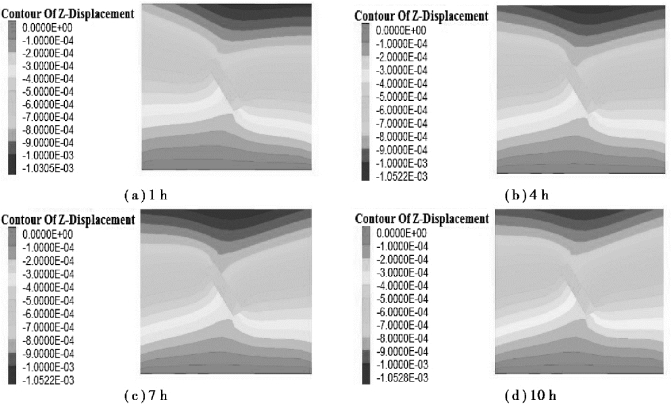
图4.26　60°节理试件x-z平面纵向变化规律

图4.27是以试件顶面中心单元为例的纵向蠕变曲线,由图可知,随着轴向荷载的施加,试件产生了0.8 mm的瞬时变形量。试件的初始蠕变阶段发生在0～2 h内,其间试件纵向蠕变速率随着时间的增加而降低,蠕变曲线主体呈下凹形,当t=2 h时,试件纵向蠕变速率达到最小值。试件的等速蠕变阶段发生在2～10 h内,蠕变量随着时间缓慢递增并最终趋于稳定。蠕变曲线近似直线,最终蠕变量为1.05 mm。

图4.28是试件在轴向压缩蠕变过程中,横向的蠕变变形云图。由图可知,试件因预应力锚杆的作用,锚端位置的横向变形范围由试件底部向顶部移动。随着蠕变时间增加,预应力锚固效果减弱,节理面变形明显,试件沿节理两端发生变形角度为60°的剪切变形,变形特征较为明显。

图4.27　60°节理试件纵向蠕变曲线

图4.28　60°节理试件x-z平面横向变化规律

图4.29为x=0断面中心点横向蠕变曲线。由图可知,随着轴向荷载的施加,试件横向并未随即产生瞬时变形。待锚杆预应力值损失至0,t=0.6 min后,试件产生了0.092 mm的瞬时变形量。试件的初始蠕变阶段发生在0～4 h内,其间试件横向蠕变速率随着时间的增加而降低,蠕变曲线主体呈下凹形,当t=4 h时,试件纵向蠕变速率达到最小值。试件的等速蠕变阶段发生在4～10 h内,试件横向蠕变量趋于稳定。最终蠕变量为0.233 mm。相对90°节理试件,其初始变形及最终变形值均增加,进入等速蠕变阶段时间减小。60°节理面使试件x方向剪切变形增加,进入等速蠕变阶段时间增加。

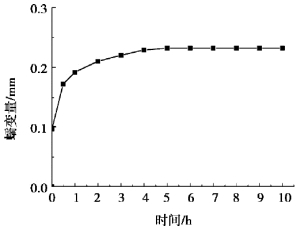
图4.29　60°节理试件横向蠕变曲线

如图4.30所示,由接触面剪切变形可以观察到,其左侧顶部及右侧底部变形最为明显,由于节理角度与水平方向成60°,受到轴向压力作用,节理面两侧成60°对称剪切变形发展。

图4.30　60°节理试件接触面变形

(3)30°倾角节理试件蠕变规律

如图4.31所示,取1,4,7,10 h平面纵向变形云图分析,从x-z平面轴向蠕变变形趋势可以看出,由于预应力锚杆的锚固效果,在试件施加荷载的初始阶段,试件顶部V字区分布不均匀,偏向试件尾部分布。由于节理弱面的存在,相同水平位置,节理纵向变形较大。随着蠕变时间的增加,试件轴向蠕变量趋于均匀。说明随着蠕变变形过程,预应力锚杆的锚固效果呈减弱趋势。节理面的存在,使试件整体变形呈两边向中心递增的趋势,并且节理面增加了变形范围。相比60°轴向变形,其蠕变值减小。

图4.32是以试件顶面中心单元为例的纵向蠕变曲线,由图可知,随着轴向荷载的施加,试件产生了0.72 mm的瞬时变形量。试件的初始蠕变阶段发生在0～2 h内,其间试件纵向蠕变速率随着时间的增加而降低,蠕变曲线主体呈下凹形,当t=2 h时,试件纵向蠕变速率达到最小值。试件的等速蠕变阶段发生在2～10 h内,蠕变量随时间缓慢递增并最终趋于稳定。蠕变曲线近似直线,最终蠕变量为0.95 mm。

图4.31　30°节理试件x-z平面纵向变化规律

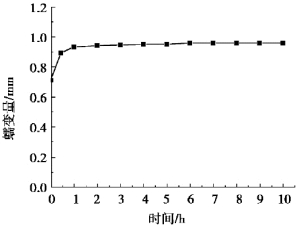
图4.32　30°节理试件纵向蠕变曲线

图4.33取试件在轴向压缩蠕变过程中1,4,7,10 h平面横向蠕变云图分析,由图可知,试件由于预应力锚杆的作用,试件变形趋势由顶部向底部发展。随着蠕变时间的增加,预应力锚杆锚固效果逐渐减弱,试件沿节理面端部变形,最终变形趋向30°剪切变形,变形特征较为明显。

图4.34为x=0断面中心点横向蠕变曲线。由图可知,随着轴向荷载的施加,试件横向并未随即产生瞬时变形。待锚杆预应力值损失至0,t=1 min后,试件产生了0.081 mm的瞬时变形量。试件的初始蠕变阶段发生在0～3 h内,其间试件横向蠕变速率随着时间的增加而降低,蠕变曲线主体呈下凹形,当t=3 h时,试件纵向蠕变速率达到最小值。试件的等速蠕变阶段发生在3～10 h内,试件横向蠕变量趋于稳定。最终蠕变量为0.22 mm。

图4.33　30°节理试件x-z平面横向变化规律

由图4.35接触面剪切变形可以看出,其左侧顶部及右侧底部变形最为明显,由于节理角度与水平方向成30°,受到轴向压力作用,节理面两侧最终成30°发生剪切变形。对比分析3种角度条件下节理面变形趋势,试件整体变形以节理面滑移为主,最终发生明显的压剪破坏。

图4.34　30°节理试件横向蠕变曲线

图4.35　30°节理试件接触面变形