加锚岩体蠕变变形及锚杆预应力损失耦合效应模型研究

1)弹性元件

弹性元件由一个弹簧组成,用来模拟理想的弹性体,如图4.11所示,其本构规律服从虎克定律,即

式中　E——弹性模量,Pa;

σ——应力,Pa;

ε——应变。

图4.11　弹性元件示意图

2)黏性元件

黏性元件由一个带孔活塞和充满黏性液体的圆桶组成,又称阻尼器,如图4.12所示,用来模拟理想的黏性体,其本构规律服从牛顿定律,即

分离变量积分后,得

式中　η——动力黏滞系数,Pa·s;

t——时间,h;

σ0——初始应力,Pa。

图4.12　黏性元件示意图

3)塑性元件

塑性元件由一对摩擦片构成,如图4.13所示用来模拟完全塑性体,其本构规律服从库伦摩擦定律。塑性体受力后,当应力小于其屈服极限时,物体不产生变形,当应力一旦达到或超过屈服极限σs时,便开始持续不断地流动变形。

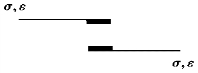
图4.13　塑性元件示意图

4)Maxwall模型

Maxwall模型由弹性元件和黏性元件串联而成,如图4.14所示。通常用来模拟软硬相间的岩体在垂直侧面加载条件下的本构规律。

Maxwall模型的本构方程为

研究模型的蠕变特性,使σ为常量,模型蠕变方程为

图4.14　Maxwall模型

Maxwell模型的蠕变曲线如图4.15所示。在t=0时,模型具有瞬时变形。

图4.15　Maxwall模型的蠕变曲线

5)Kelvin模型

Kelvin模型由弹性元件和黏性元件并联构成,如图4.16所示。Kelvin模型常用来模拟软硬相间的层状岩体在平行层面加荷时的本构规律。

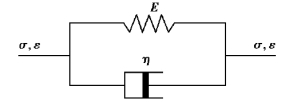
图4.16　Kelvin模型

Kelvin模型本构方程为

当σ为常量时,Kelvin模型的蠕变方程为(www.xing528.com)

Kelvin模型蠕变曲线如图4.17所示,可知Kelvin模型不具有瞬时变形。

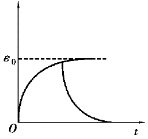
图4.17　Kelvin模型的蠕变曲线

岩体流变模型采用广义开尔文(General Kelvin)模型,该模型由弹簧和Kelvin模型串联组成,其本构方程为

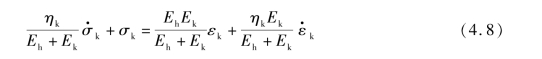
式中　Eh——瞬时弹性模量,Pa;

Ek——滞后弹性模量,Pa;

Es——锚杆弹性模量,Pa;

ηk——黏滞系数,Pa·h。

广义开尔文模型对模拟岩石的黏-弹性具有一定的优势,同时该模型具有模拟岩石瞬时弹性变形的优点。

考虑岩体蠕变与锚杆预应力损失耦合效应,将代表锚杆弹性元件与广义开尔文体并联,表征锚-岩协同变形。其模型如图4.18所示。

图4.18　加锚无节理岩体蠕变变形与锚杆预应力损失耦合效应模型

对于假定岩体为各项同性的均质体,锚杆预应力均匀分布在均质岩体上,锚杆的弹性模量可以等效转化为

式中　El——锚杆实际弹性模量,Pa;

As——锚杆体截面面积,cm2;

Ar——锚杆体侧向有效锚固范围内岩体截面面积,cm2。

设定锚杆的弹性模量随时间变化的损失函数为

用来表征轴向压力对侧向锚杆预应力损失程度,则

当t=0时,E′s=Es,则b=1,E′s=Es(at+1)。

考虑锚-岩协同变形机制以及其耦合关系,则有

对式(4.14)求导,得

将式(4.15)代入本构方程:

当σ=σc=con st时,式(4.16)可转化为

进一步整理,得

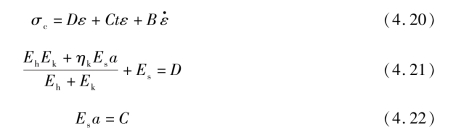
求解式:

当t=0时,岩体的弹性变形为

将式(4.24)代入式(4.23)后,得