数值模拟方案与数值模型

1)建立模型

数值分析中采用的模型尺寸为φ50×100 mm的标准试件,模型网格单元划分为100×200=20 000个,如图2.54所示,将模型看成平面应力问题来研究,试件节理材料破坏准则选择莫尔-库伦准则,细观力学参数符合Weibull分布随机赋值。在通过大量数值模拟分析以及参考了大量文献发现均值度m取值为3时,室内试验结果与数值分析结果比较接近,故RFPA中以m=3的取值进行不同节理分布的模拟试验研究。

图2.54　试件模型图

数值模拟分为单轴压缩试验、单轴循环加载试验两部分。由单轴压缩试验得出的试件基本力学参数经公式转换成数值分析中基元的力学参数,宏观峰值强度和弹性模量通过公式来确定数值模拟中的细观参数[67],其计算式分别为

式中　E细观和f细观——在软件内输入的数值,即Weibull分布的细观抗压强度和细观弹性模量值,Pa;

E宏观和f宏观——在室内试验中试件宏观抗压强度和宏观弹性模量,Pa。(www.xing528.com)

根据式(2.21)、式(2.22)来计算细观参数值,在软件中重复进行完整试件单轴压缩实验,对每次试验结果输入的参数进行微调,最后得出与室内试验完整试件宏观抗压强度和弹性模量相近的细观参数值,试验中的相变准则参数控制参数取值见表2.16,试件细观力学参数见表2.17。

表2.16　相变准则参数控制参数

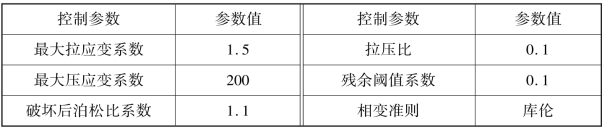
表2.17　试件细观力学参数

2)加载参数设置

建立数值模型之后,进行加载参数设置,加载方式选择Y轴负向位移增量的分步位移控制,在单轴加载模型中每步加载位移量为0.002 mm,在单轴循环加载模型中加载位移量为0.002 mm/步,卸载位移量为0.002 mm/步。