单轴压缩试验的力学特性分析

(1)应力应变曲线分析

单轴压缩试验作用下的应力-应变曲线反映出试件的强度特征和变形性质,试件应力-应变曲线由试验数据统计得出并绘制如图2.10所示。不同节理分布的试件力学参数均低于完整试件,与节理分布方式密切相关。完整试件应力应变曲线单轴抗压强度为74.86 MPa,弹性模量为29.47 GPa,其破坏形式为轴向劈裂拉伸破坏,表现为典型的脆性岩石,在受压过程中大致分为4个阶段:

第一阶段:初始压密阶段。在此阶段由于试件非均质性,在轴压逐渐增大的过程中试件内部存在的裂纹、孔隙开始闭合,释放部分能量,应力应变曲线斜率逐渐增大,表现出非线性上升变形特征。

第二阶段:弹性变形阶段。应力应变曲线几乎呈现线性上升的特征,由于内部仍有一些缺陷存在,初期预制节理周围基本无破坏出现。随着应力的增加,预制节理周围微节理萌生,试件发生起裂现象,曲线呈现非线性上升。

第三阶段:塑性软化阶段。应力应变曲线斜率变小,随着预制节理周围沿着轴向应力方向扩展形成局部贯通破裂面,产生应力跌落现象。

第四阶段:应力峰后阶段。峰值后应力应变曲线出现了迅速的应力跌落,应变变化较小,此时裂纹快速扩展贯通,含节理试件发生脆性破坏。

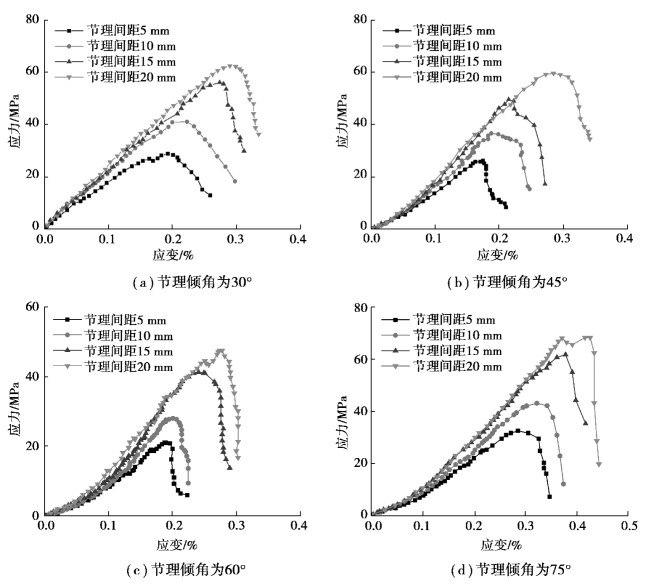
图2.10　试件的轴向应力-应变全曲线

从表2.2中可以看出,试件节理的间距、倾角对试件强度和变形有着不同程度的影响,含预制节理试件峰值强度、弹性模量及轴向应变明显降低。在一定间距范围内,节理间距越大,从初期加载到峰值应力的加载空间越大,其承载抗变形能力越强,对工程安全有重要意义。

表2.2　单轴压缩下含不同节理分布的试件力学参数

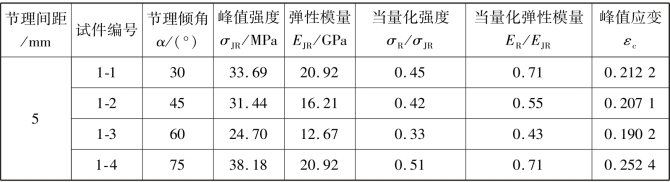
续表

为分析和探讨节理倾角对强度和变形参数的影响,根据试件的轴向应力应变曲线得出在不同节理间距和倾角下的峰值强度和弹性模量,单轴压缩下含不同节理分布的试件力学参数见表2.2,引入以下两个无量纲化参数[61]:

①当量化弹性模量EJR/ER时,定义为含节理试件的弹性模量EJR与无节理试件的弹性模量ER之比。

②当量化强度σJR/σR时,定义为含节理试件的强度σJR与无节理试件的强度σR之比。

(2)强度特征随节理倾角和节理间距的变化规律

从峰值强度随节理倾角与节理间距的变化曲线图中可以得出:

不同节理间距下试件的峰值强度随节理倾角表现出的随着节理倾角先减小后增大的趋势,其曲线形式呈现U形,试件的峰值强度小于完整试件,这是不同的节理分布发生不同程度的变形所致,30°和75°倾角试件的峰值强度较大,表现出节理试件各向异性特征。

从图2.11中可以看出,当节理倾角小于60°时,峰值强度逐渐减小;当节理倾角在30°～45°时,峰值强度降低幅度较小;当节理倾角在45°～60°时,峰值强度降低幅度较大;当节理倾角在60°～75°时,峰值强度增大到最大值。在间距为5 mm时,峰值强度增大幅度为54.57%;在间距为20 mm时,峰值强度增大幅度为44.76%。当倾角为60°的试件强度降低速率最快,在节理间距为5 mm达到最小值为24.70 MPa,当量化强度达到0.33,在倾角为75°时峰值强度最大值达到68.27 MPa;当量化强度达到0.91,在倾角为30°,45°和75°处时峰值强度总体变化幅度不大。

从图2.12中可以看出,节理试件峰值强度随节理间距的增大而逐渐增大,节理间距与峰值强度之间存在明显的非线性关系。当节理倾角一定时,峰值强度在不同的节理间距下,增大速率不一致,当节理间距为5 mm和10 mm时,峰值强度随节理间距的增大而增长速度较快;当节理间距为15 mm和20 mm时,峰值强度随节理间距的增大而增加较慢。当节理倾角为30°时,节理间距从5 mm增至10 mm时,峰值强度从33.69 MPa增至41.17 MPa,峰值强度增大幅度为22.20%,节理间距从15 mm增至20 mm时,峰值强度从56.15 MPa增至62.13 MPa,峰值强度增大幅度为10.65%,当节理倾角为75°时,峰值强度随节理间距的增大而增长速度最快,当s=20 mm时,峰值强度增大为68.27 MPa。

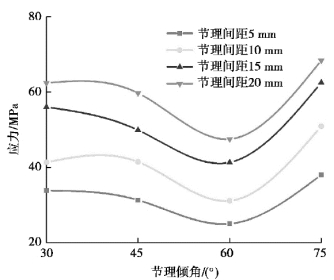
图2.11　峰值强度随节理倾角变化曲线

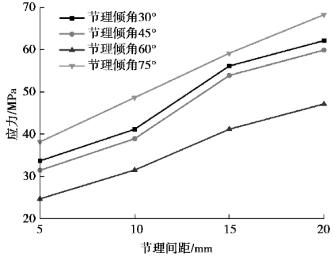
图2.12　峰值强度随节理间距变化曲线

从图2.13中可以看出,当节理倾角为30°,节理间距s由5 mm分别增大为10,15,20 mm时,相应的节理当量化峰值强度值由0.45分别增大到0.55,0.75,0.83,变化幅度为84.4%,均小于完整试件强度值。当量化峰值强度变化分别为22.2%,66.67%,84.4%,从数据中可以得出,节理倾角和间距的不同分布对试件强度和变形能力有着不同程度的影响,其中峰值强度变化最大值为84.4%,说明在节理面作用下,试件变形过程中峰值强度变化最大。当量化峰值强度随节理间距的增大而增大时,它们之间存在明显的非线性关系,试件的当量化峰值强度与节理间距可通过指数函数拟合,通过数据拟合获得相似性方程:

式中　σJR,σR——含节理与完整试件的单轴压缩峰值强度,Pa;

A,B,C——拟合函数。

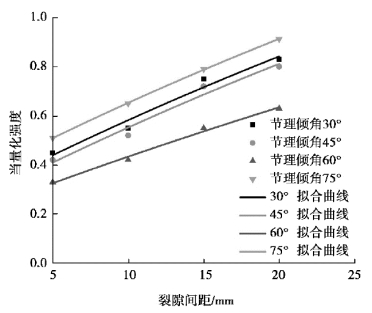
图2.13　不同节理间距下当量化峰值强度拟合曲线

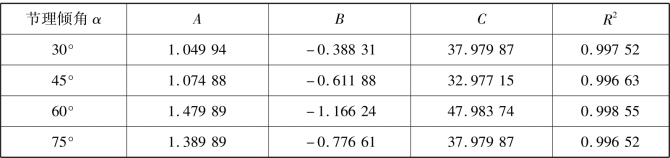
在不同节理倾角下,表2.3列出了节理试件当量化强度随节理间距变化的各拟合曲线的参数、相关系数R2。

表2.3　当量峰值强度与节理间距关系回归参数(www.xing528.com)

(3)变形参数随节理倾角与节理间距的变化规律

从弹性模量随节理倾角与节理间距的变化曲线图中(图2.14、图2.15)可以得出:

不同节理间距下节理试件的弹性模量随节理倾角同样表现出随着节理倾角先减小后增大的趋势,其曲线形式呈现U形,试件的弹性模量小于完整试件。

从图2.14中可以看出,当节理倾角小于60°时,弹性模量逐渐减小;当节理倾角在30°～45°时,弹性模量降低幅度较小;当节理倾角在45°～60°时,弹性模量降低幅度较大;当节理倾角在60°～75°时,弹性模量增大到最大值。在间距为5 mm时,弹性模量变化幅度为65.11%,在间距为20 mm时,弹性模量变化幅度为31.02%。当倾角为60°时试件强度和弹性模量降低速率最快,试件强度达到最小值,弹性模量达到极小值12.67 GPa,当量化弹性模量降低为0.43、倾角为75°时,弹性模量最大值达到27.41 GPa;当量化弹性模量降低为0.93时,节理倾角整体变化幅度不大。

从图2.15中可以看出,试件弹性模量随节理间距的增大而逐渐增大,节理间距与弹性模量之间存在明显的非线性关系,弹性模量在不同的节理间距下增长速率不一致。当节理间距为5 mm和10 mm时,弹性模量强度随节理间距的增大而增长速度较快;当节理间距为15 mm和20 mm时,弹性模量随节理间距的增大而增长速度较慢。当节理倾角为30°、节理间距从5 mm增至10 mm时,弹性模量从20.92 GPa增至22.10 GPa,弹性模量增大幅度为5.64%,节理间距从15 mm增至20 mm时,弹性模量从23.28 GPa增至24.17 GPa,弹性模量增大幅度为3.82%。当节理倾角为75°时,弹性模量随节理间距的增大而增长速度最快,当s=20 mm时,弹性模量增大为27.41 GPa。

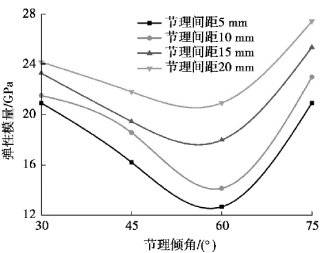
图2.14　弹性模量随节理倾角变化曲线

图2.15　弹性模量随节理间距变化曲线

从图2.16中可以看出,当节理倾角为30°,节理间距s由5 mm分别增大为10,15,20 mm时,相应的节理当量化弹性模量值由0.71分别增至0.75,0.79,0.82,变化幅度为15.49%,均小于完整试件强度值,当量化弹性模量变化分别为5.63%,11.27%,15.49%时,从数据中可以看出,节理倾角和间距的不同分布对试件强度和变形能力有着不同程度的影响,说明在节理面作用下,试件变形过程中峰值强度变化最大。当量化弹性模量随节理间距的增大而增大时,它们之间存在明显的非线性关系,试件的当量化弹性模量与节理间距可通过指数衰减函数拟合,通过数据拟合获得相似性方程:

式中　EJR,ER——含节理与完整试件的单轴压缩弹性模量,Pa;

A,B,C——拟合参数。

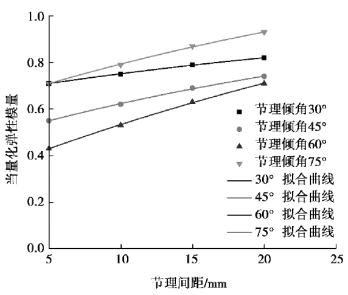
图2.16　不同节理间距下当量化弹性模量拟合曲线

在不同节理倾角下,表2.4列出了节理试件当量化弹性模量随节理间距变化的各拟合曲线的参数、相关系数R2。

表2.4　当量弹性模量与节理间距关系回归参数

(4)峰值应变随节理倾角和间距的变化规律

峰值应变随节理倾角、节理间距变化曲线如图2.17、图2.18所示。由图2.17可以看出,峰值应变随倾角变化曲线呈现出U形,与峰值强度规律保持一致,说明随着峰值强度的增大,试件的延展性越好,其承载安全性越强。不同节理倾角下的峰值应变值从大到小依次为75°＞30°＞45°＞60°,在节理倾角为60°时,峰值应变值降至0.19%,均小于其他倾角对应的峰值应变值。由图2.18可以得出,在各节理间距下,峰值应变变化幅度不大,且随着节理间距的增大,应变值逐渐增大,说明峰值强度也越来越大。峰值应变随着节理间距的增大而增大,它们之间存在明显的线性关系,试件的峰值应变与节理间距可通过一次函数拟合,如图2.19所示,通过数据拟合获得相似性方程:

式中　A,B——拟合参数。

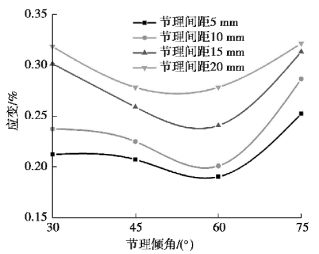
图2.17　峰值应变随节理倾角变化曲线

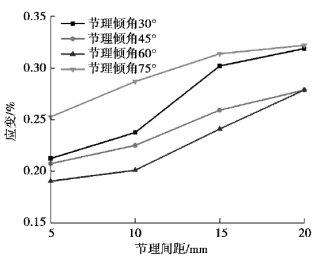
图2.18　峰值应变随节理间距变化曲线

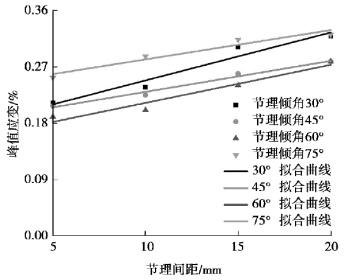
图2.19　不同节理间距下峰值应变拟合曲线

在不同节理倾角下,表2.5列出了节理试件当量化弹性模量随节理间距变化的各拟合曲线的参数和相关系数R2。

表2.5　峰值应变与节理间距关系回归参数