非旋转对称自由曲面整形透镜的优化设计

1.非旋转对称自由曲面整形透镜设计基本原理

除了圆形孔径的光束，矩形孔径的光束也是一种比较普遍的光束。矩形孔径的光束作为一种非旋转对称的光束，只能采用非旋转对称的自由曲面透镜进行整形。针对非旋转对称光束，同样采用单片自由曲面整形透镜，其前表面为平面，后表面为自由曲面。如图10-10a所示，入射光束为一个矩形孔径的准直光束，光束入射到透镜的平面上经过自由曲面透镜折射后，在目标面上产生一个辐照度均匀分布的矩形光斑，自由曲面透镜的孔径也是一个矩形。矩形光束整形的原理为：将输入光束的截面按等能量划分为N×M个网格，目标面按等面积划分为N×M个网格，控制输入光束每个网格的能量经过自由曲面后，入射到目标面上对应的网格，如图10-10b所示。这样目标面上每个网格的能量相同，每个网格的面积又相等，目标面辐照度就可以变得均匀。

图10-9 目标面辐照度分布

a）整形前光束辐照度分布 b）整形后光束辐照度分布

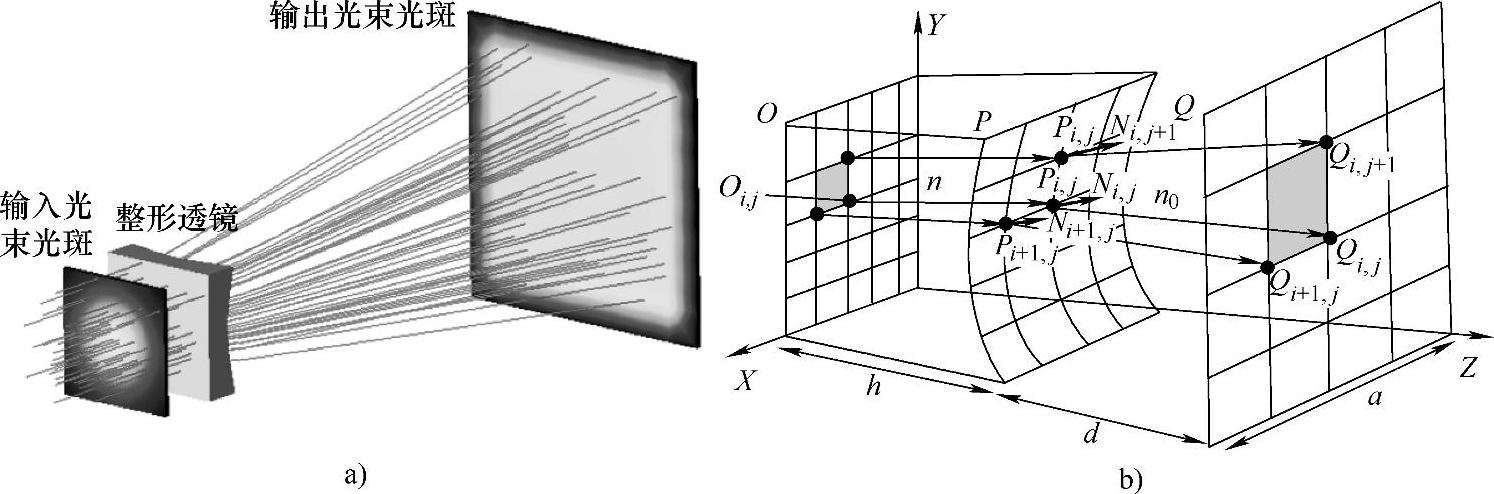
图10-10 准直激光光束整形系统示意图

2.非旋转对称自由曲面整形透镜设计过程

按上述整形原理，设计用于矩形光束整形的自由曲面透镜算法主要分为三步：第一步，对激光光束按等能量进行网格划分，同时对目标面按等面积进行网格划分。第二步，根据边缘光线理论，建立光源与目标面之间的能量映射关系；构建自由曲面相邻两个采样点之间的迭代关系，计算自由曲面上的采样点。第三步，建立自由曲面透镜模型，进行光线追迹，验证设计结果。

（1）将光束和目标面分别按等能量和等面积分割

首先，对入射光源进行等能量网格划分。采用的入射光源为矩形孔径准直激光光束，在光束的束腰截面上，将截面进行等能量划分，划分为N×M份，如图10-11a所示。

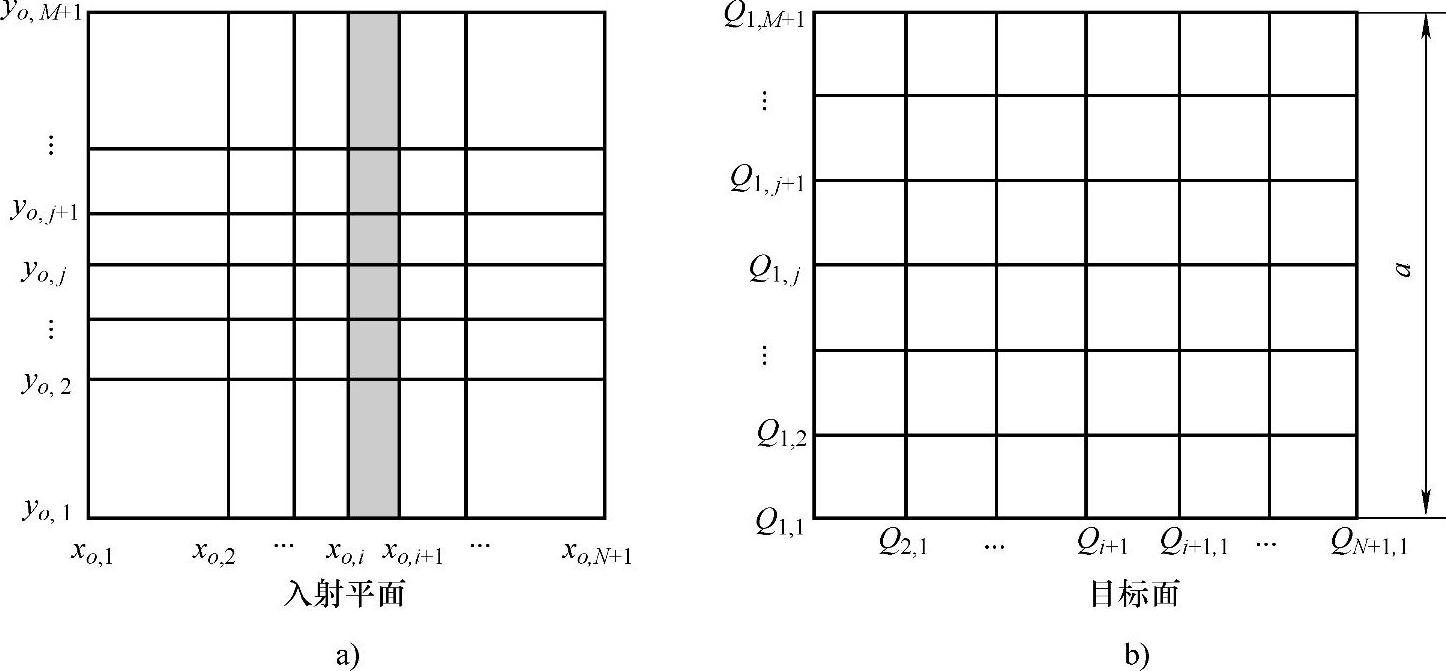
图10-11 将光束和目标面进行网格化

a）光源入射截面能量网格划分示意图 b）目标面网格划分示意图

入射激光束在X、Y两个方向上的发光强度均呈高斯分布，因此对激光光束总能量计算时可进行变量分离，则入射光束的总能量为(www.xing528.com)

光束在X轴方向上的单位能量Φ_o（x）为

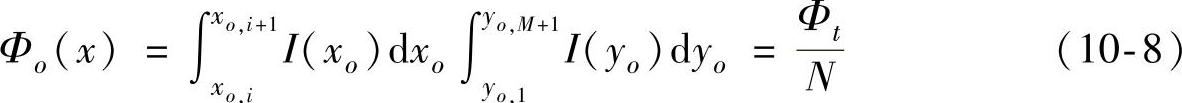
联立式（10-7）、式（10-8），可得到光源所有能量网格格点横坐标x_o，i（i=1，2，…，N+1），同理，利用式（10-7）、式（10-9）可以求得所有网格格点纵坐标y_o，j（j=1，2，…，M+1）。

目标面Q为矩形平面，在x和y轴方向的边长分别为a和b。将目标面按等面积划分，将其划分为N×M份，如图10-11b所示，很容易计算目标面上任意网格格点的坐标Q_i，j（x_i，y_j）：

（2）构建自由曲面相邻采样点之间的迭代关系

透镜的前表面为平面，透镜的后表面为自由曲面，设计主要是针对自由曲面进行的。透镜前表面O和出射面P具有相同的网格，各网格点的横纵坐标相等，即x_p，i=x_o，i，y_p，j=y_o，j（i=1，2，…，N+1；j=1，2，…，M+1）。因此要得到透镜自由曲面P的面形，只需求出自由曲面P各网格点的Z轴坐标即可。

Z轴坐标的求解方法如图10-10b所示。沿Z轴方向，光线O_i，jP_i，j先从透镜前表面入射，经过透镜折射后，光线沿着P_i，jQ_i，j方向出射。透镜折射率为n，由折射定律矢量式（10-6），可求出光线O_i，jP_i，j在P_i，j点的法向量N_i，j，这样可以得到过P_i，j点的切平面。假设划分的网格数量足够多，那么可近似认为与光线O_i，jP_i，j相邻光线O_i+1，jP_i+1，j交于过P_i，j点的切平面上，且交点为P_i+1，j，则法向量N_i，j与向量P_i，jP_i+1，j垂直，由此就能很容易地找到交点P_i+1，j和P_i，j+1的Z轴坐标递推关系式：

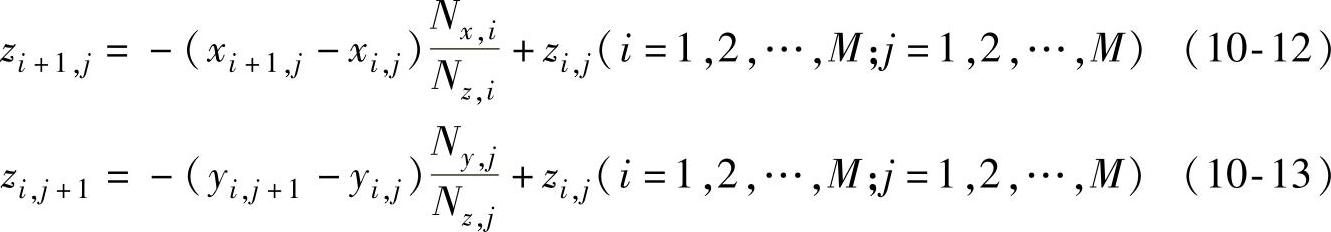
给定透镜初始厚度h，即z_1，1，根据上述递推关系式即可得到自由曲面上所有采样点的坐标。

（3）设计实例

针对10mm×10mm的矩形孔径准直激光光束设计一个自由曲面整形透镜，具体的设计参数如下：透镜初始厚度h为3mm，透镜折射率n为1.4935，透镜距目标面距离d为100mm，目标面边长a为40mm，网格划分数为100×100。基于这些参数，利用上面介绍的设计方法，设计的自由曲面透镜如图10-12所示。其中图10-12a为自由曲面的1/4部分，因为矩形孔径的自由曲面透镜为1/4对称结构，所以设计自由曲面的1/4部分，通过对称即可获得整个自由曲面。图10-13a和b分别为激光光束直接照射目标面的辐照度分布和经过自由曲面整形透镜后的辐照度分布。经过自由曲面透镜整形后，激光光束在目标面的辐照度均匀度为90.5%。