旋转对称自由曲面整形透镜设计技巧

1.旋转对称自由曲面整形透镜设计基本原理

设计自由曲面整形透镜的基本思想就是将激光光束按等能量分割成N个子光束，将目标面面积等分为N份，控制每个子光束入射到对应的目标区域，这样就可以在目标面上产生均匀的激光辐照度分布，如图10-4所示。由于设计的透镜为旋转对称的自由曲面透镜，所以只需要针对其截面轮廓进行设计就可以。然后将这一轮廓作为一条母线进行旋转就可以得到最后的透镜了。整形透镜使用了单个自由曲面，前表面为平面，后表面为自由曲面。

图10-4 旋转对称自由曲面整形透镜设计原理图

2.自由曲面整形透镜设计过程

实现圆对称辐照度均匀分布的自由曲面整形透镜设计主要分为两步：第一步，将激光光束按等能量分为N个子光束，同时将目标面划分为N个等面积的同心圆环，由边缘光线理论，建立光源与目标面之间的能量映射关系；第二步，由斯涅尔定律，计算自由曲面整形透镜的面形数据以及法向矢量，构建自由曲面整形透镜。

（1）将光束和目标面分别按等能量和等面积进行划分

首先，对激光器出射的激光光束进行等能量分割，本节讨论的是光束呈旋转对称的情况，因此对光束能量的划分只需要讨论光束一个截面轮廓如图10-5所示。该图表示了光束的一半口径，光束的全口径范围是-x_n～x_n。

光束的发光强度分布为高斯分布，故截面上的发光强度分布为

图10-5 激光光束等能量划分示意图

式中，ω₀为激光束的束腰宽度。

入射光束的总能量为

将入射到X轴正方向上的光线按等能量划分为N份，则入射光束在X轴方向上每份能量为

根据式（10-3）可以得到将激光光束等能量分割时的分割点x_i，可以将过分割点上的每条光线作为采样光线在计算自由曲面透镜轮廓时使用。

接下来将对目标面进行按等面积划分，目标面为一个圆形平面，目标面的半径为R，将目标面划分为N个等面积同心圆环，如图10-6所示，设每个圆环的半径为r_i（i=1，2，…，N），每个圆环的面积为S₀，可得(www.xing528.com)

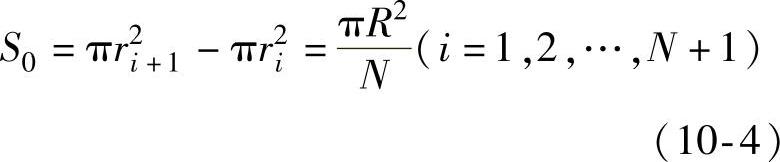
每个圆环的半径为

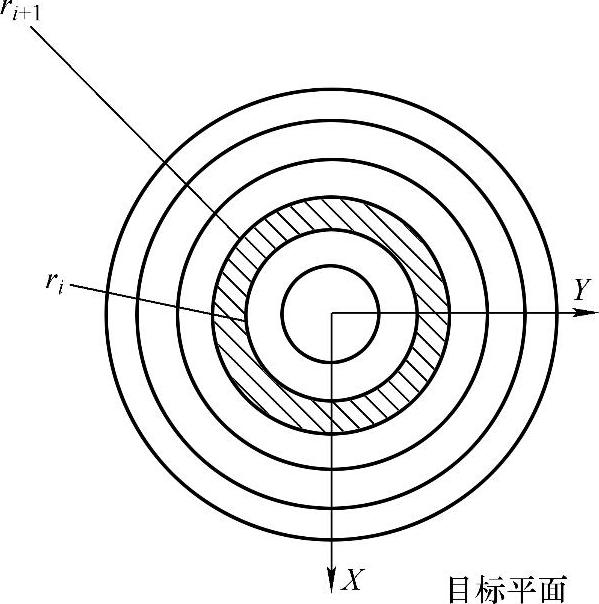
图10-6 将目标面按等面积划分示意图

这样，目标面已被等面积划分为N个圆环单元。

（2）计算透镜轮廓上相邻两个点之间的迭代关系

如图10-7所示，透镜的第一面（下表面）为平面，第二面（上表面）为自由曲面，所以设计是针对上表面进行的。实现圆对称光斑辐照度均匀，只需确保子光束的边缘光线能够投射到对应的面积单元的边缘位置，也就是说在光束截面上，通过M_iM_i+1区域的光束，经自由曲面透镜折射后，投射到了Q_iQ_i+1区域，如图10-7所示。这样就建立了光束和目标面的能量映射关系。计算透镜上表面轮廓时，首先要确立透镜上表面中心点的位置P₁，要控制入射光线M₁P₁经过P₁点后出射到Q₁点，这样可以确定入射光线矢量M₁P₁和出射光线矢量P₁Q₁。利用折射定律矢量形式[式（10-6）]可以确定过P₁点的法向矢量N₁。

[1+n²-2n（Out·In）]^1/2·N=Out-nIn （10-6）

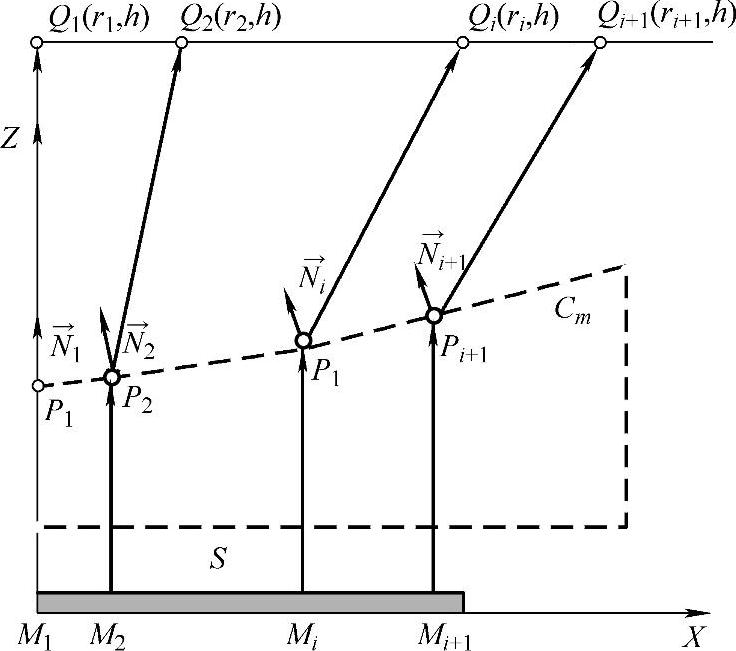
图10-7 计算自由曲面轮廓的原理示意图

式中，In和Out分别为入射光线和出射光线的单位方向矢量；N为光线入射到自由曲面上某点P的单位法向矢量；n为自由曲面透镜材料的折射率。在获得了过P₁点的法向矢量N₁后，进一步可以获得过P₁点的切线。计算过P₁点切线与第二条采样光线的交点为P₂点，第二条光线经过P₂点入射到Q₂，这样可以确定第二条入射光线矢量M₂P₂和出射光线矢量P₂Q₂，这样可以确定过P₂点的法向矢量N₂，计算过P₂点切线与第三条采样光线的交点为P₃点。按照这种迭代方法可以计算自由曲面母线上的所有采样点，确立自由曲面透镜的母线，旋转对称获得自由曲面透镜。

3.设计实例

根据上面介绍的算法，针对圆形孔径光束设计了一个自由曲面整形透镜，具体的设计参数如下：束腰为10mm，透镜折射率为1.495，透镜中心厚度为10mm，透镜到目标面的距离为100mm，目标面半径为20mm。根据这些参数计算得到的自由曲面透镜母线和实体模型如图10-8所示。

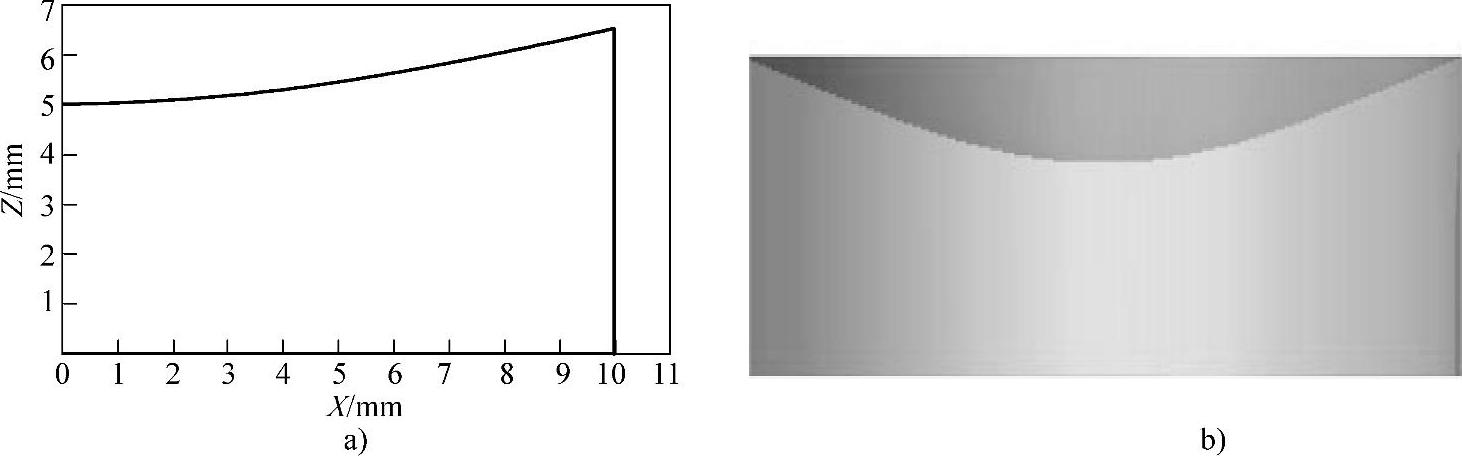
图10-8 旋转对称自由曲面整形透镜母线及实体图

a）自由曲面透镜的母线 b）自由曲面透镜的实体模型

图10-9为激光光束整形前后的辐照度分布。其中图10-9a为激光器直接输出光束的辐照度分布，图10-9b为激光光束经过自由曲面透镜整形后的辐照度分布，通过计算可知激光光束经整形后在目标面有效区域内的辐照度均匀度可达90%。