双反射太阳能集光系统实现辐照度均匀分布设计方案

使用单个抛物面反射器可以有效地会聚太阳光在太阳电池表面，然而无法使太阳光在电池表面产生均匀的辐照度分布。双反射太阳集光系统可以有效解决这一问题。双反射太阳集光系统是一个旋转对称的结构，因此可以只设计一个二维面形轮廓，然后通过旋转对称来形成最后的实体模型。双反射太阳集光系统的光路图的二维视图如图8-7所示，太阳光经过P面和M面两次反射后，入射到了太阳电池的表面。为了控制入射到太阳电池表面的辐照度分布比较均匀，设计思路如下：首先将入射到反射面P的太阳光按等能量进行划分，太阳光是均匀的，故将入射光束的截面按等面积划分为N个区域。通过截面等分点的光线入射到反射面P上，反射面P也对应分为N个区域，每个区域将一部分光会聚到太阳电池上的某个特定的采样点。在太阳电池上选N个采样点，这N个采样点对应着N个采样半径，这些采样半径刚好把太阳电池的表面分成了等面积的同心圆环。当N取得数量足够大时，太阳光照射在太阳电池表面的光分布就越均匀。

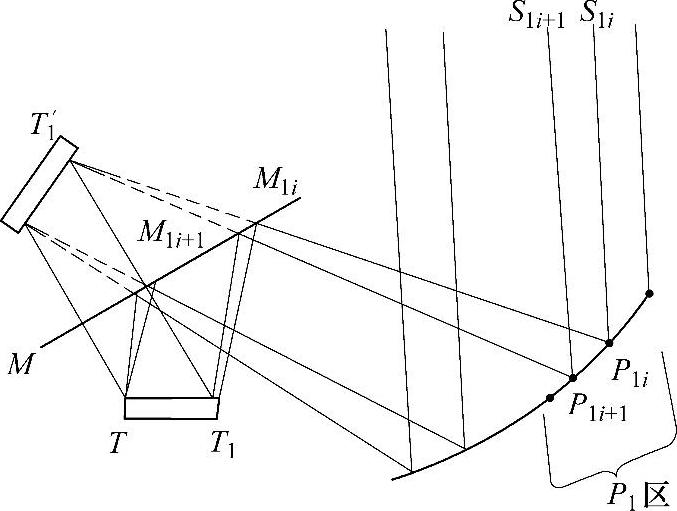
图8-7 双反射太阳集光系统光路示意图

先计算P面上的第1个区域，这里称为P₁区，P₁区的光经过M面反射后直接到达了电池的T₁点，因为M面是一个平面反射面，所以为了计算简便，可以等效为P₁区的光直接入射到了T₁点的镜像点的位置T′₁。先要计算出太阳电池表面上各采样点的镜像点，假设太阳电池上的某个采样点T_q的位置为（x_q，y_q），反射面M的方程（二维情况为一直线）为

y=mx+b （8-5）

该反射面的位置是初始时候确定的，故m、b都是确定的。T_q的位置为（x_q，y_q）也是确定的，这样可以求其关于平面反射面的镜像位置T′_q（x′_q，y′_q），T_q和T′_q是镜像对称的，故满足

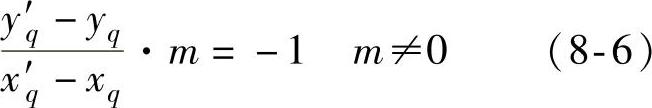
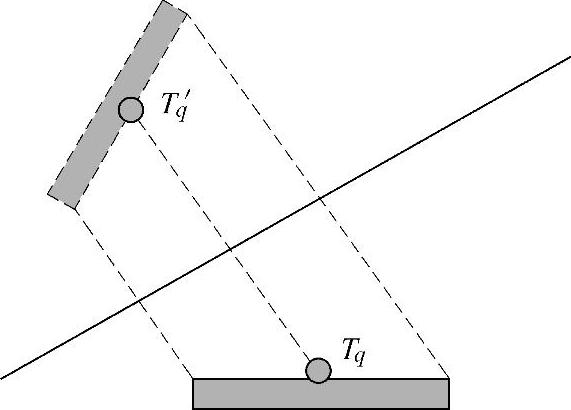
图8-8 太阳电池上的采样点的镜像位置

此外

联立式（8-6）和式（8-7）可以计算出T′_q的横纵坐标为

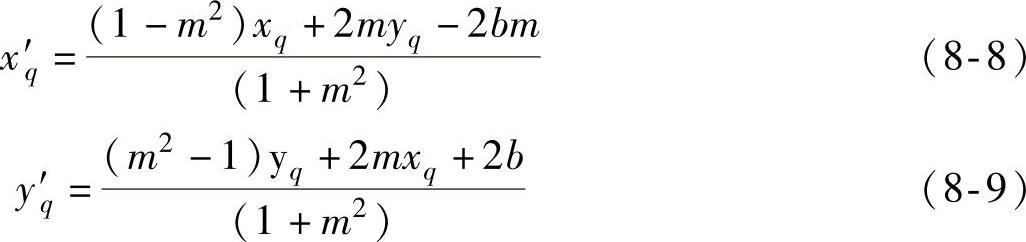
根据式（8-8）和式（8-9）可以求得所有的镜像点。

接下来求P面上第一区域内（P₁区）上各点的坐标，P₁区上各采样点选取的是将光束进行等能量分割的那些点，所有采样点的横坐标都是已经确定的，接下来就是讨论求解各采样点的纵坐标。假设P₁区上的P_1i点已知，构建P_1i（x_1i，y_1i）和其相邻采样点P_1i+1（x_1i+1，y_1i+1）之间的迭代关系可以求得P_1i+1，有了这种迭代关系就可以从起始点依次迭代计算求出该区域内所有点的坐标。接下来就讨论如何构建P_1i（x_1i，y_1i）和P_1i+1（x_1i+1，y_1i+1）之间的迭代关系。

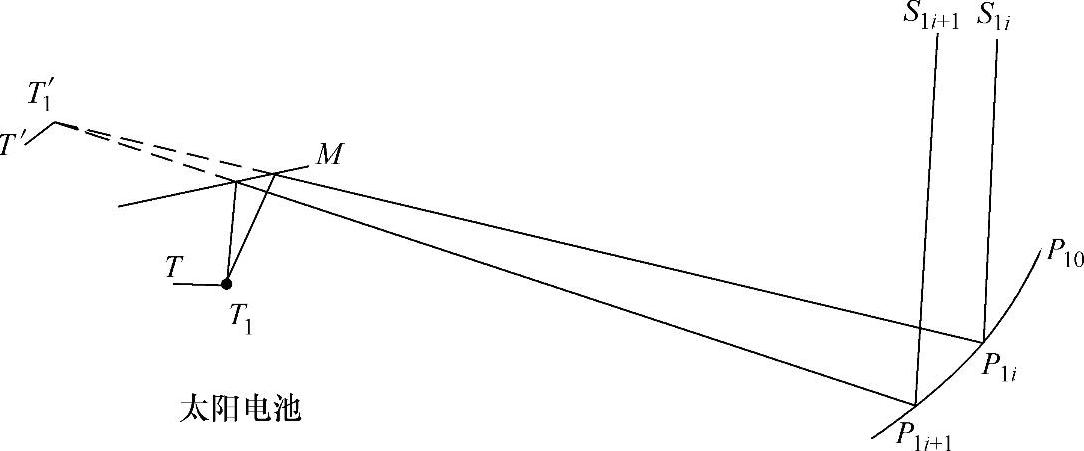
图8-9 P₁区内光线传播示意图

如图8-9所示，入射到P面上的P₁区内的光线经过两次反射后入射到了太阳电池上的采样点T₁处。采样光线S_1iP_1i入射到P₁区上的P_1i点，该入射光线可以用一单位矢量表示如下：

I_1i=[0，-j] （8-10）

经过P_1i点反射光线的矢量为(www.xing528.com)

Out_1i=[（x′₁-x_1i）i，（y′₁-y_1i）j] （8-11）

对矢量进行归一化有

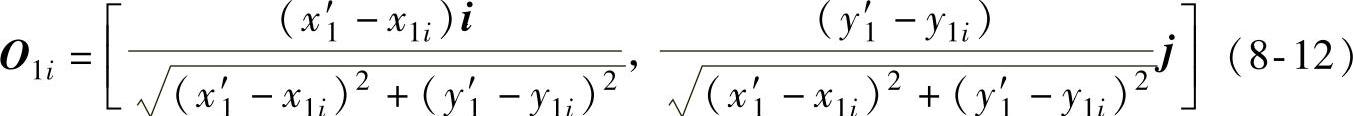
根据反射定律的矢量形式有

Out-In=[2-2（Out·In）]^1/2N （8-13）

可以求得过P_1i点的法向矢量

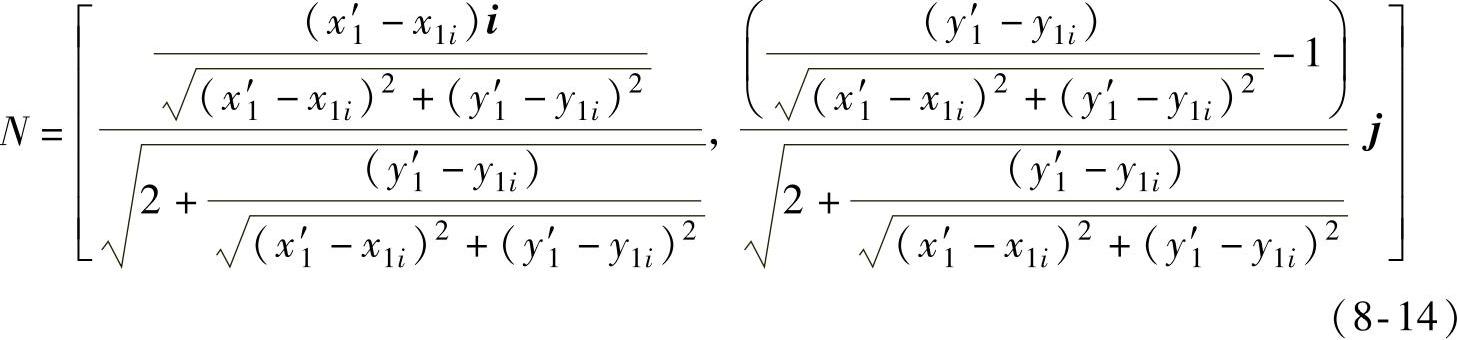
根据法向矢量可以求得过P_1i点的切线斜率为

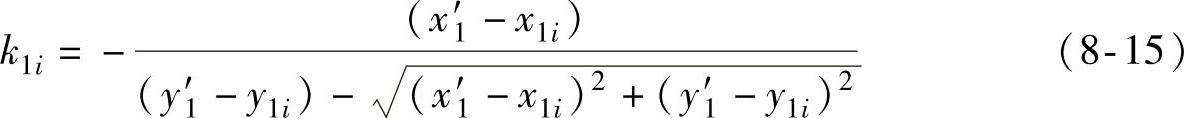
过P_1i点的切线与相邻的光线的交点为P_1i+1，这样过P_1i点的切线斜率又可以表示为

式中，（x_1i+1，y_1i+1）为P_1i+1点的坐标，其中x_1i+1为已知的，因此需要求P_1i+1点的纵坐标。联立式（8-15）和式（8-16）即可求得y_1i+1如下：

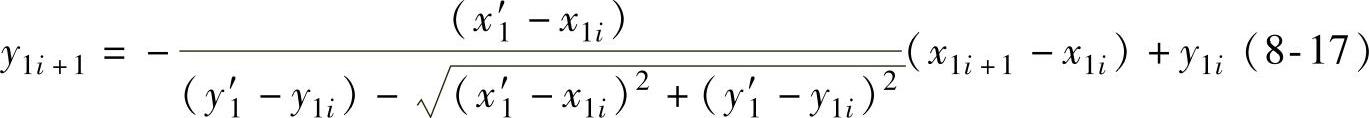
可以看出P_1i+1点的纵坐标与以下几个量有关系：①太阳电池上采样点T₁的镜像点（x′₁，y′₁）；②P_1i的坐标点（x_1i，y_1i，）；③P_1i+1点的横坐标。其中T₁点的镜像点（x′₁，y′₁）及P_1i+1点的横坐标都是选取半径分割点，都是确定的，所以一旦P_1i的纵坐标y_1i确定以后，P_1i+1点的纵坐标就可以计算出来，这样就找到了相邻两个采样点之间的迭代关系了。由于初始点P₀的坐标是确定的，故利用这种迭代关系可以求得该区域内所有点的纵坐标。重复上面的过程可以计算反射面P区内任意一个区域P_i上的所有采样点。使用这种方法设计了一个双反射太阳集光系统，设计结果的二维轮廓图及光线分布如图8-10所示。使用双反射系统，太阳光在电池表面产生了均匀的辐照度分布如图8-11所示。

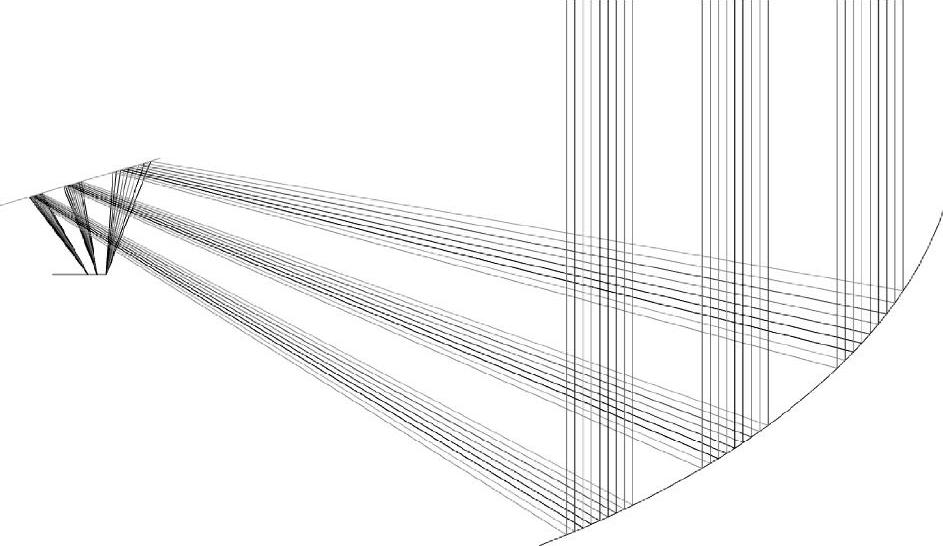
图8-10 双反射光学系统的二维轮廓图及光线分布

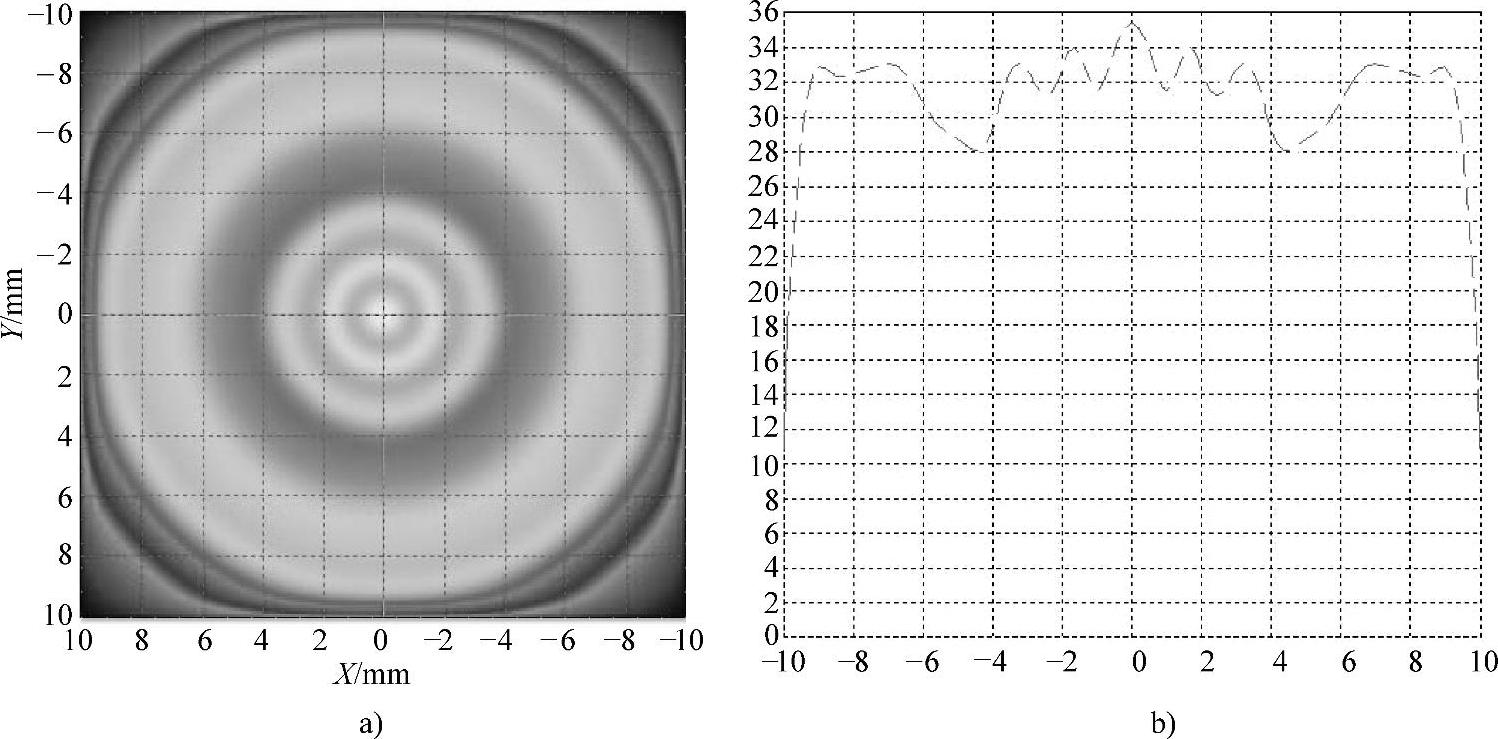
图8-11 太阳电池上的辐照度分布