球形LED阵列：对称分布的照明方案

这个阵列包含了12颗相同的LED，阵列中的每颗LED是一个完美的朗伯光源。这12颗LED分布在两个环上，每个环上分布6颗LED，这两个环处于不同的两个截面上，如图6-3所示。每个环上的6颗LED是等角间隔分布在该环上。两个环上对应的LED之间有一定的错位，假设角间隔为Δφ。

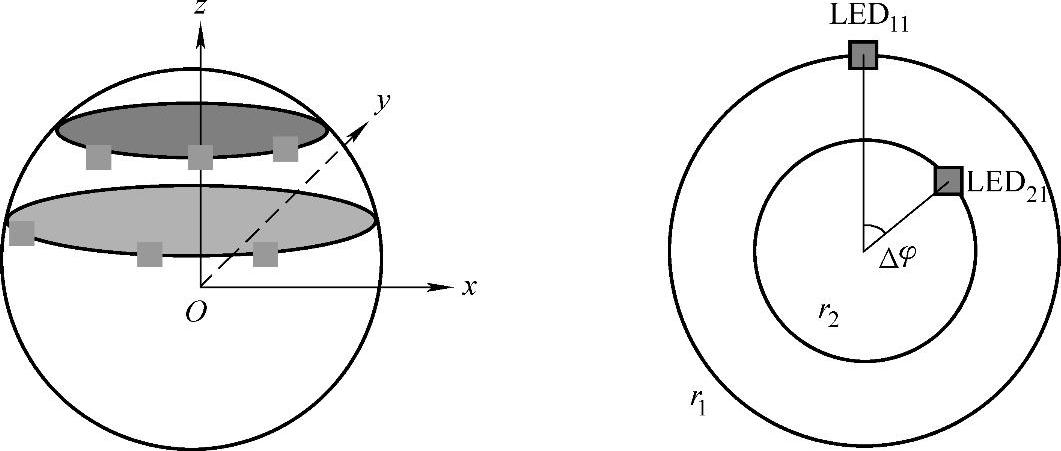
图6-3 球面上两环LED阵列分布的二维和三维示意图

根据图6-4a可以计算两个环的半径分别为

r₁=Rsinθ₁，r₂=Rsinθ₂ （6-10）

第一个环（下面）的第k个LED坐标分别为（X_1k，Y_1k，Z_1k），第二个环（上面）的第k个LED坐标分别为（X_2k，Y_2k，Z_2k），n为每个环上的LED颗数。

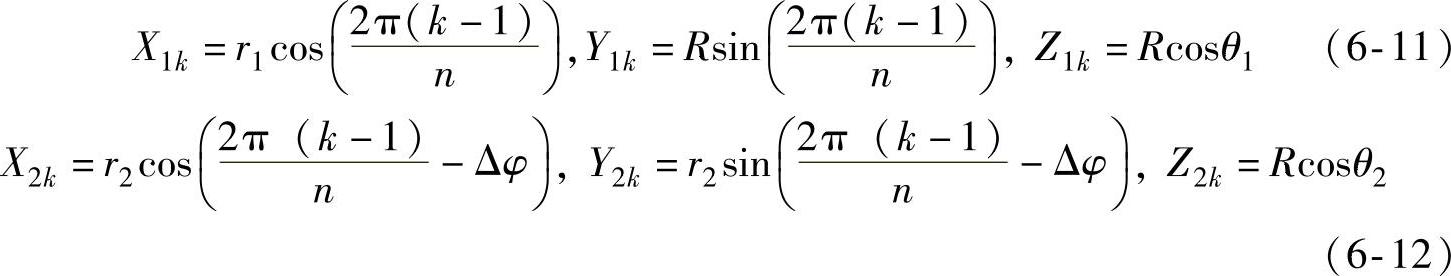
这12颗LED形成的球形阵列在目标面上任一点（x_i，y_j，z）产生的辐照度分布如下：

根据辐照度分布函数式（6-13）和式（6-9）可以构建该阵列优化的评价函数，评价函数中的自变量为每颗LED的坐标，阵列中每颗LED与3个变量（θ₁，θ₂，Δφ）有关系，这3个变量表示的意义可以参考图6-4。本案例优化过程中的初始条件如表6-1所示。

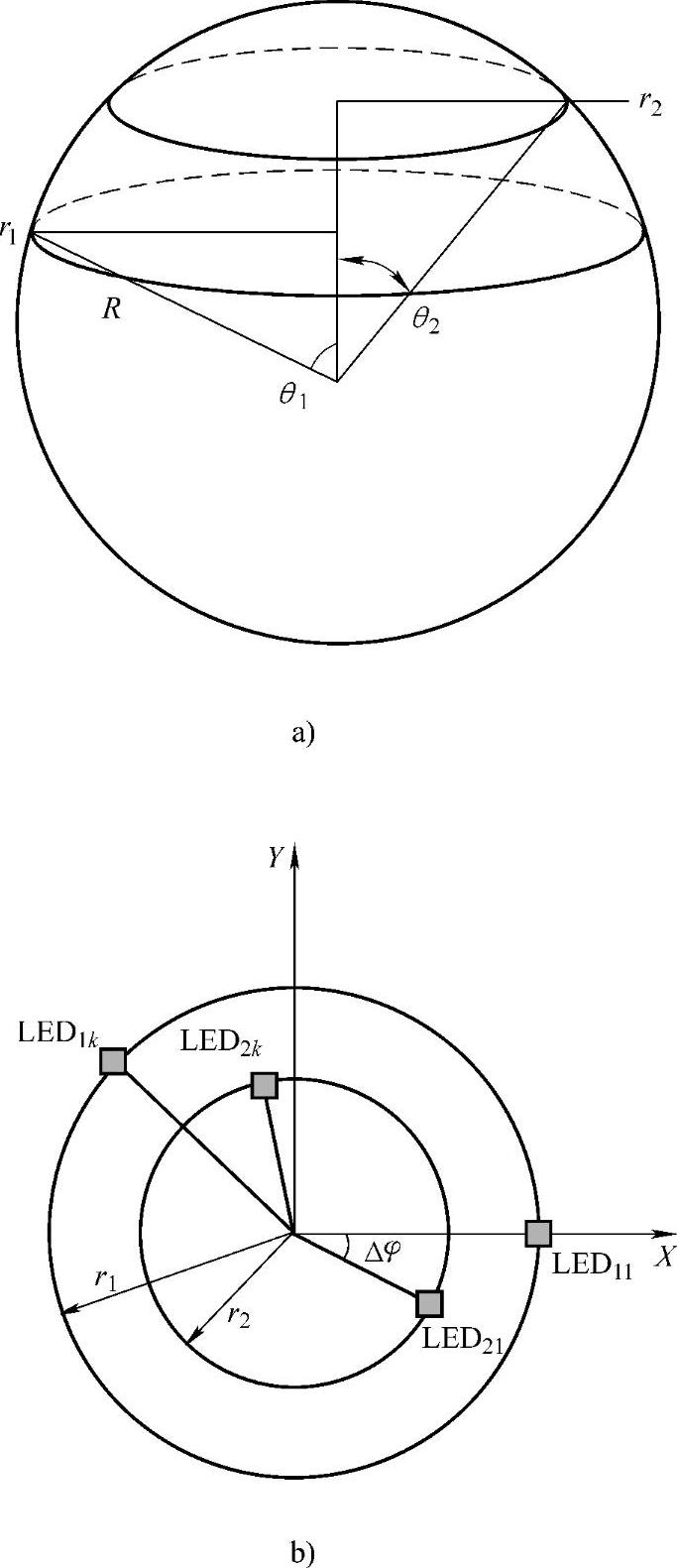
图6-4 LED位置坐标计算示意图(www.xing528.com)

表6-1 球形阵列优化的初始条件

经过优化，得到了三个变量的最优值分别为θ₁=24.7°，θ₂=29.9°和Δφ=30°。图6-5a为优化后的LED阵列。这个优化后的LED阵列在x-y平面的投影如图6-5b所示。阵列1中的第1颗LED与阵列2中的第1颗LED之间的间隔Δφ=30°。

图6-5 对称分布在球面上的LED阵列优化之后的排布图

a）三维视图 b）二维视图

优化后的LED阵列在目标面上产生了均匀的辐照度分布和轮廓如图6-6所示，经过计算目标面上的辐照度均匀度达到了94%。

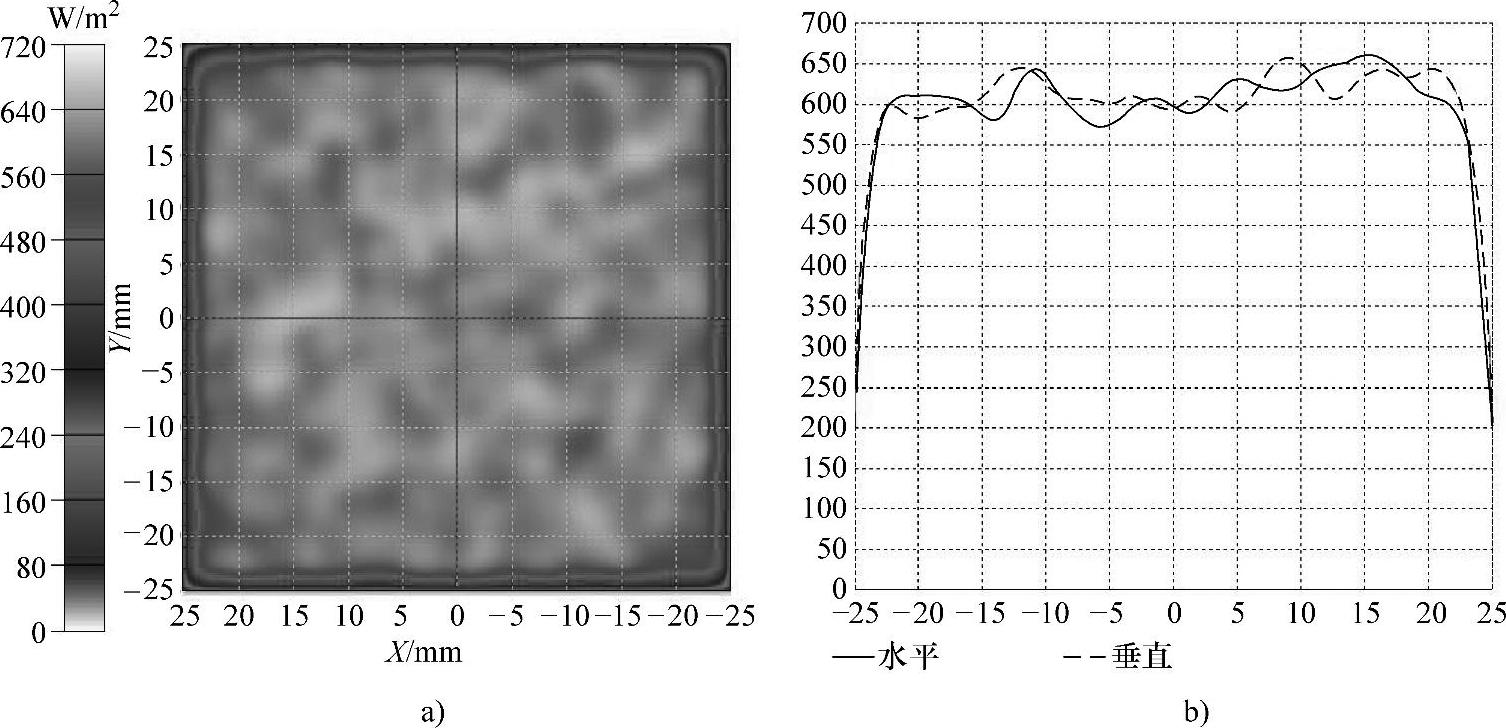
图6-6 对称分布的球形阵列优化之后的辐照度分布和轮廓

a）辐照度分布 b）辐照度轮廓