球形LED阵列设计理论优化探讨

首先分析当单颗LED位于球面上任意一点，在目标面上产生的辐照度分布，如图6-1所示。坐标原点O点是球面的球心，LED位于球面上的P点，球面的半径为R，P点的坐标是（X_k，Y_k，Z_k），P点的坐标满足

X²_k+Y²_k+Z²_k=R² （6-1）

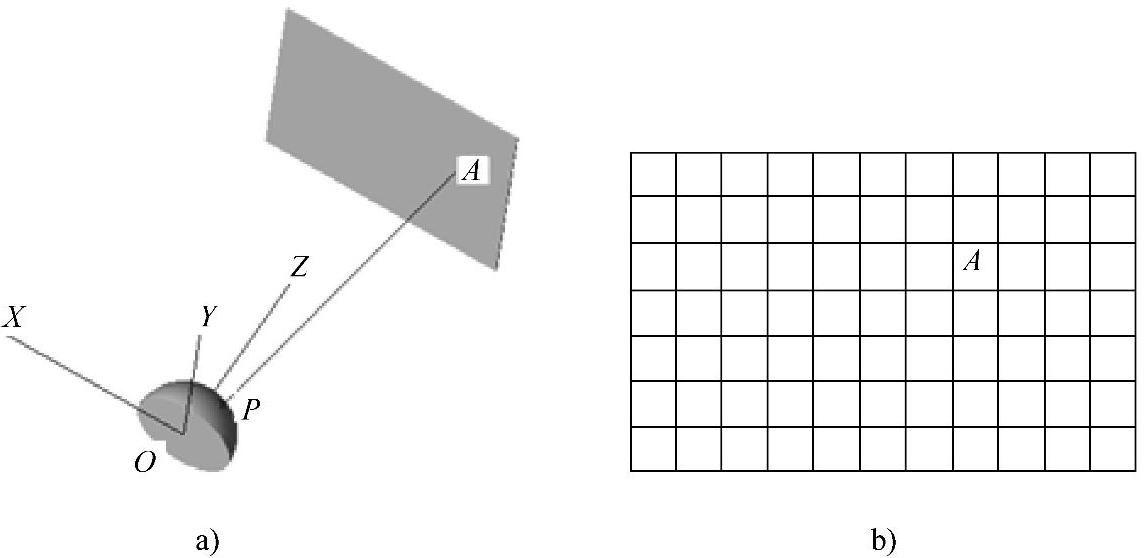
图6-1 固定于球面上的单颗LED照明系统示意图

目标面被分成M×N采样网格如图6-1b所示。假设目标面上有任意一点A其坐标为（x_i，y_j，z）。矢量OP为LED的法向矢量，用矢量PA来表示从光源所在位置P点出射的并照到目标面上A点的光线。矢量OP和PA可以用下式来表示：

OP=X_ki+Y_kj+Z_kk （6-2）

PA=（x_i-X_k）i+（y_j-Y_k）j+（z-Z_k）k （6-3）

式中，i、j和k分别表示X、Y和Z方向的单位矢量。

单颗LED在A点产生的辐照度可以用下式来计算：

矢量PA表示的光线与LED的方向矢量OP的夹角为θ，I（θ）就是沿着矢量PA方向的发光强度，当LED为朗伯发光源时，其发光强度分布如式（5-1）所示。θ是矢量OP和PA之间的夹角，因此可以计算θ的余弦

将式（6-2）和式（6-3）代入到式（6-5），可以得到(www.xing528.com)

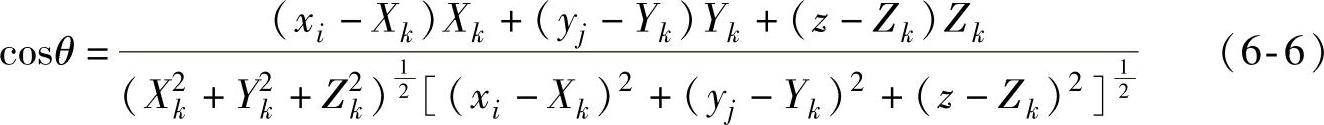
根据式（5-1）、式（6-4）、式（6-6），位于P点处的LED在目标面上的A点产生的辐照度为

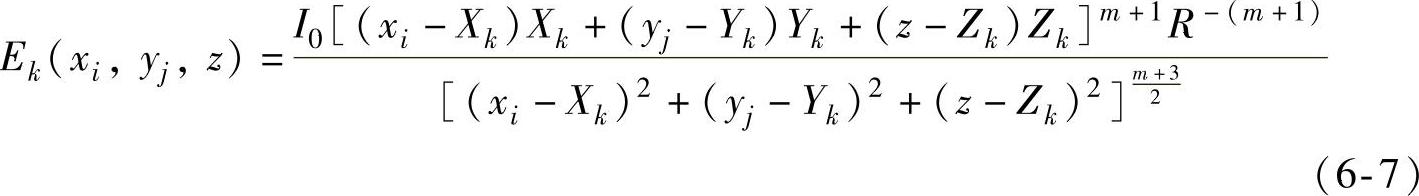
接下来我们分析由n颗LED构成的球形阵列在照明面上产生的辐照度分布。一个球形LED照明系统的示意图如图6-2所示，所有的LED都分布在球面上。

n颗LED构成的球形阵列在目标面上产生的辐照度为

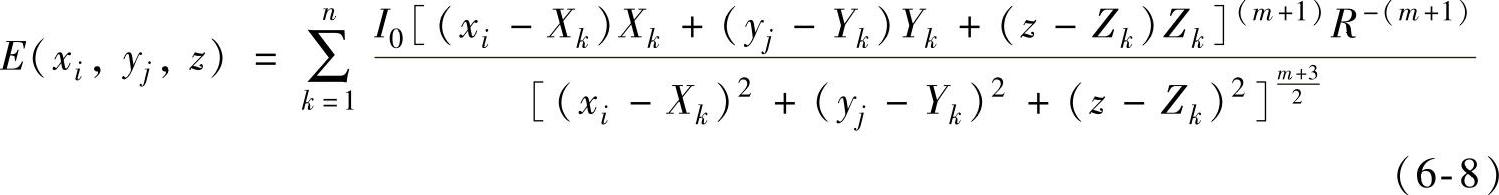
这样可以获得目标面上所有采样点的辐照度[E（x_i，y_j，z），i=1，…，M；j=1，…，N]。可以看出，辐照度是一个关于LED坐标变量（X₁，Y₁，Z₁…，X_k，Y_k，Z_k…，X_n，Y_n，Z_n）的函数。为了评价辐照度的均匀性，使用非均匀度系数（IEC 60904-9标准）作为评价函数[见式（6-9）]，评价函数的值越小，目标面上的辐照度越均匀：

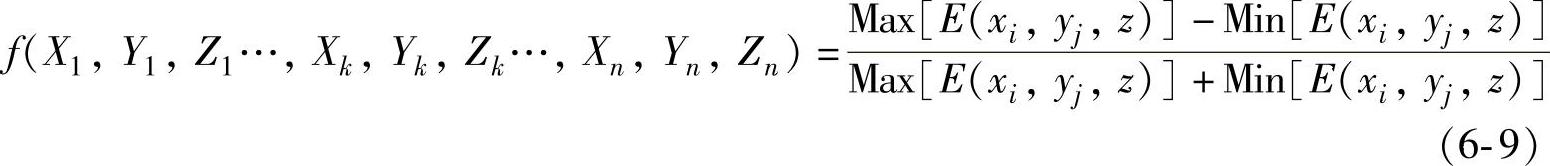
图6-2 球形LED阵列照明示意图

Max[E（x_i，y_j，z）]和Min[E（x_i，y_j，z）]是目标面上所有采样点中的最大和最小辐照度。很明显非均匀度取决于所有LED的坐标。为了产生高均匀的辐照度分布，这个评价函数越小越好。通过优化LED阵列中各LED的坐标，可以使评价函数达到最小值。这样LED阵列的优化设计问题转化为了关于评价函数最小值的搜索问题。这里使用遗传算法来寻找评价函数的最小值。