案例1：相同的LED构成的圆形阵列
图5-3是一个圆形LED阵列的示意图，设该阵列中有n颗LED等角间隔地排布在一个圆周上。这个圆形阵列中任意一颗LED的位置坐标可以确定为
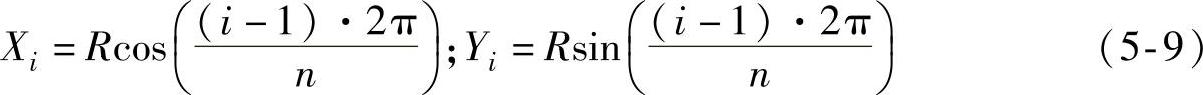
根据式（5-4）可以知道在目标面上任意一点的辐照度可以通过下式来计算：
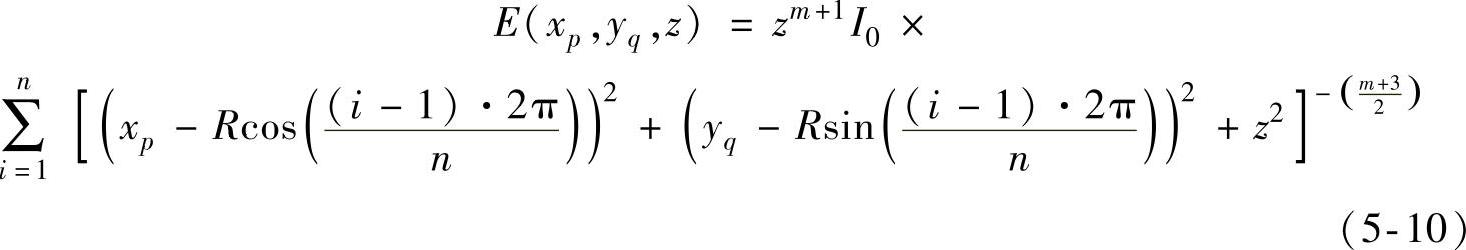
图5-3 LED圆形阵列示意图
从式（5-10）可以看出目标面上的辐照度分布取决于圆形阵列的半径R，将圆形阵列的辐照度计算公式代入评价函数式（5-6），利用模拟退火算法寻找评价数的最小值，优化变量是圆形阵列的半径。本案例设计中使用的参数如下：圆形阵列由12颗LED构成，目标面距离光源15mm，也就是z=15，目标面的大小选取的是5mm×5mm的一个方形区域。使用这些参数，利用模拟退火算法优化后，得到最佳半径值为R=11.5mm。图5-4为优化过程中，评价函数与优化次数之间的关系。当评价函数的改变量小于预先设定的改变量，优化停止。
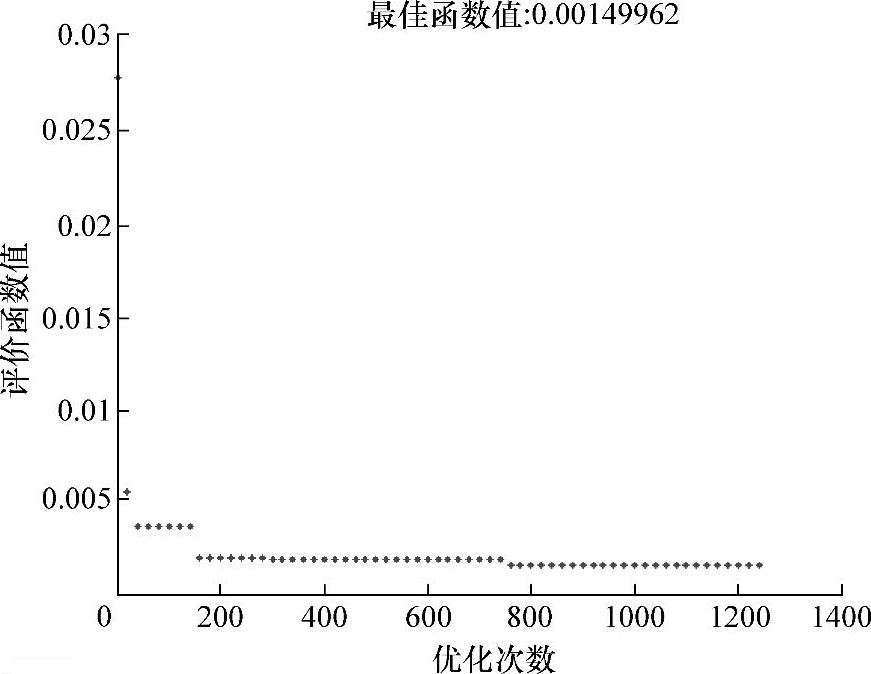
图5-4 评价函数与优化次数的关系
优化后的圆形LED阵列如图5-5所示，图5-6为优化后的圆形LED阵列照明系统图。
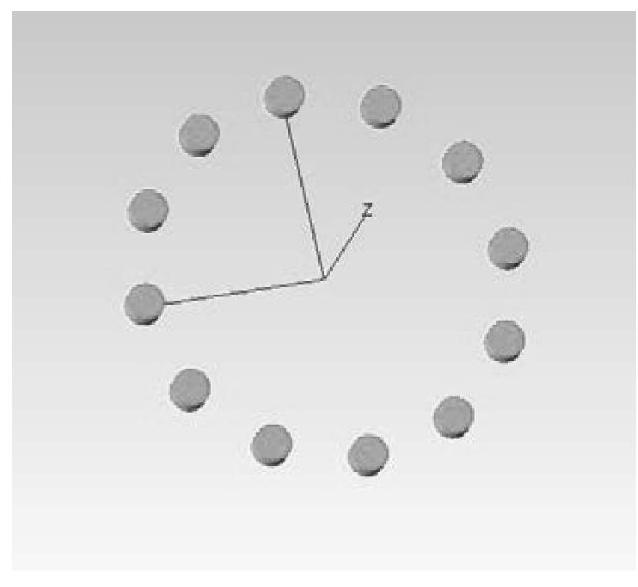
图5-5 优化后的圆形LED排列
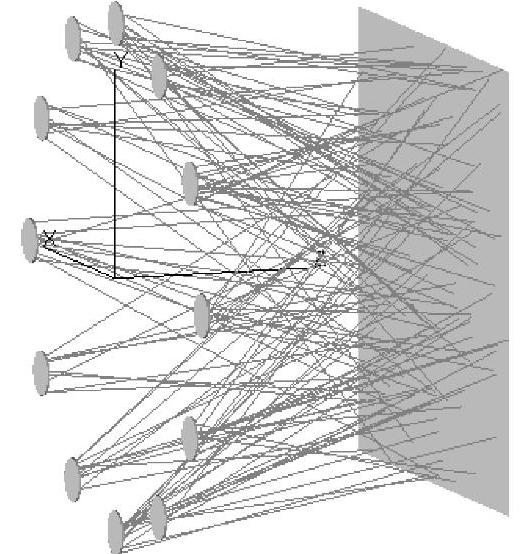
图5-6 优化后的圆形LED阵列照明系统图
图5-7为优化后的圆形LED阵列在目标面上产生的辐照度分布及轮廓，均匀度计算结果为97%。在相同的约束条件下，我们优化了不同颗数的LED构成的圆形LED阵列，图5-8是圆形阵列的最佳半径随LED颗数变化关系。我们发现这个不同颗数的LED形成的最佳阵列，其对应的最佳半径几乎是不变的。从这个图上可以看出对于圆形阵列，LED颗数的变化不会对圆形阵列的最佳半径有影响。
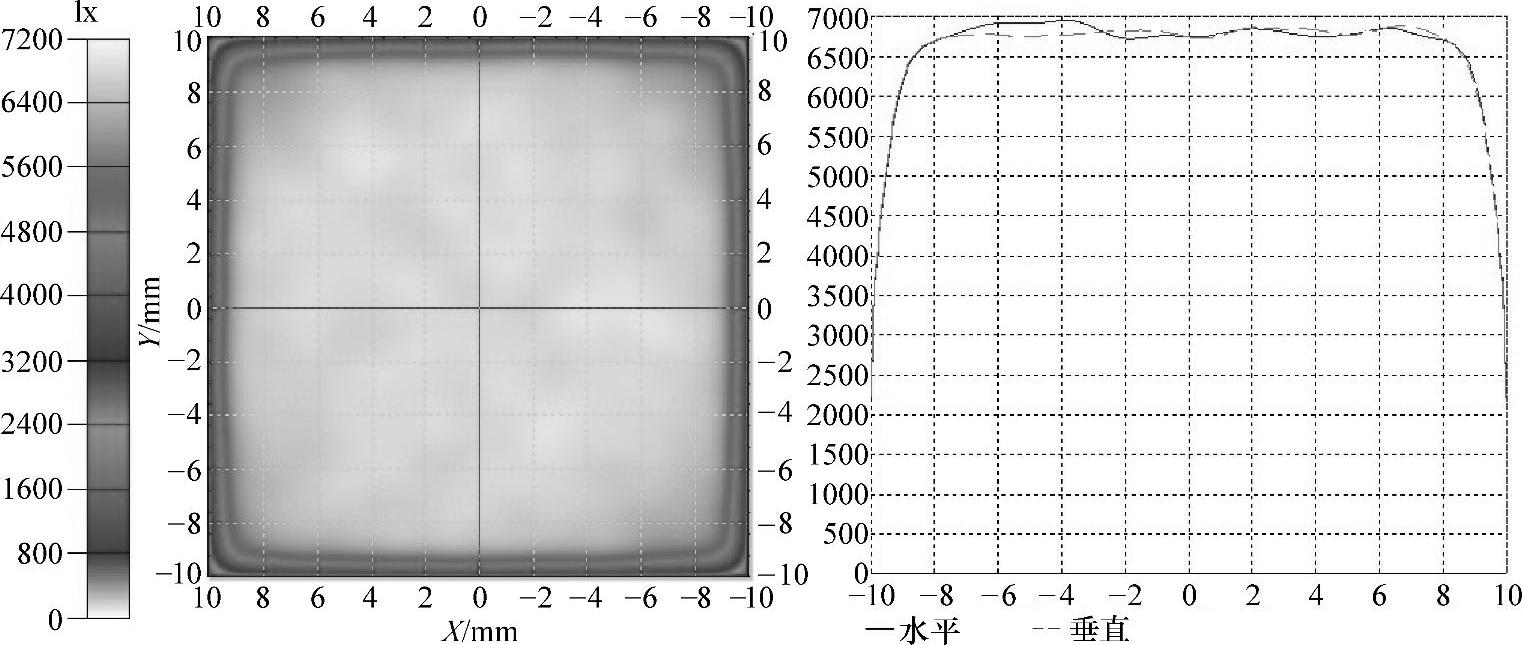
图5-7 优化后的圆形LED阵列的辐照度分布及轮廓
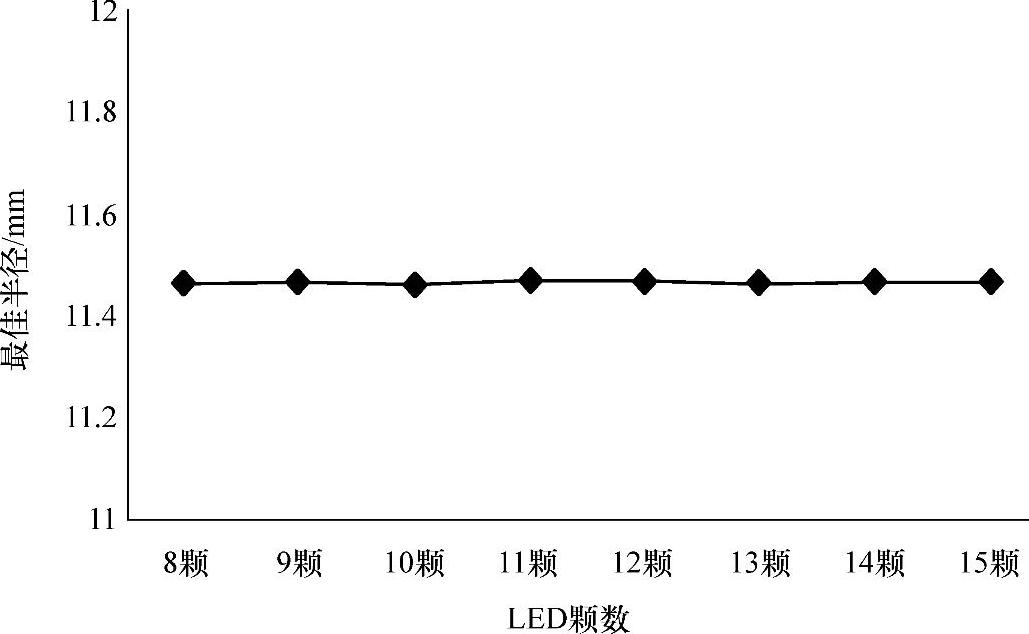
图5-8 不同颗数LED形成的圆形所对应的最佳半径值
接下来我们又分析了LED阵列平面与目标面之间的距离对最佳LED阵列半径的影响。图5-9为LED阵列平面和目标面之间的距离与最佳LED阵列半径之间的关系。可以看出最佳半径和LED阵列平面与目标面的距离几乎成正比。
案例2：由非完美朗伯分布的LED构成的圆形LED阵列
在一些情况下LED的发光强度分布呈非完美朗伯分布。本案例将设计一个圆形阵列，阵列中的每个LED发光强度分布呈非完美朗伯分布。本案例使用的每个LED前面增加了一个二次透镜，用来改变LED输出光的视角，发光强度分布变成了非完美朗伯分布。加了二次透镜和不加二次透镜的LED发光强度分布分别如图5-10和图5-11所示。比较图5-10和图5-11可以看出自由曲面透镜能将LED的视角从±90°减小到±50°。加了自由曲面透镜的发光强度分布曲线可
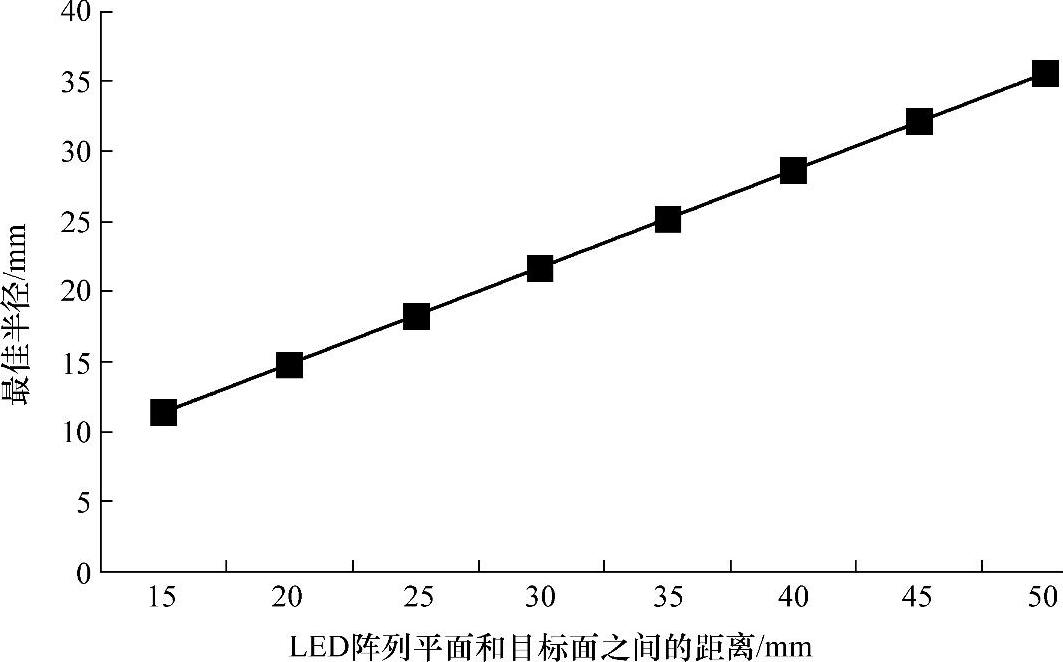
图5-9 LED阵列平面和目标面之间距离与最佳LED阵列半径的关系
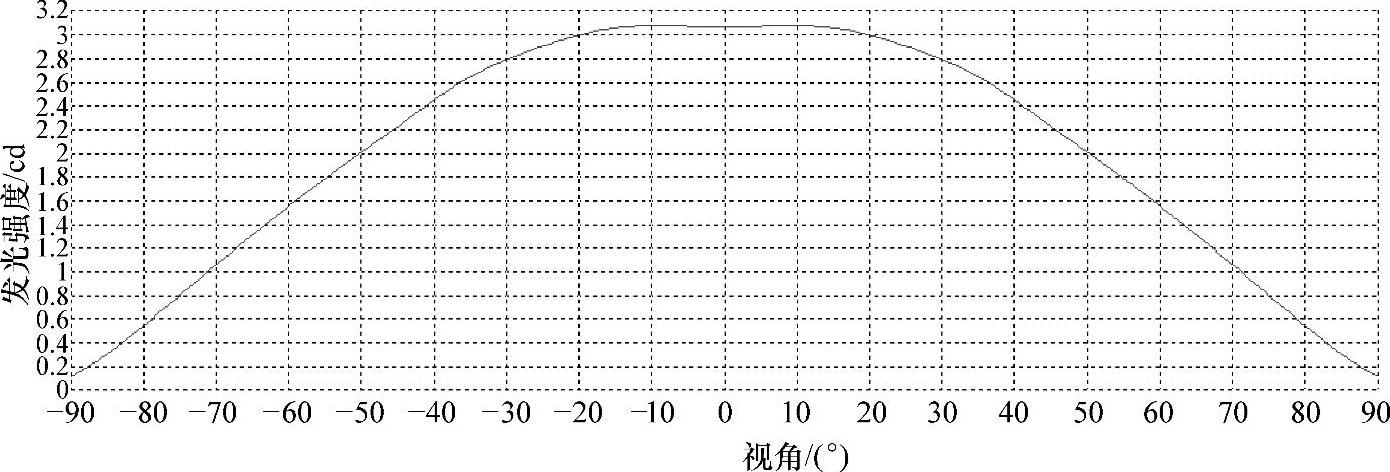
图5-10 未加自由曲面透镜时的LED发光强度分布
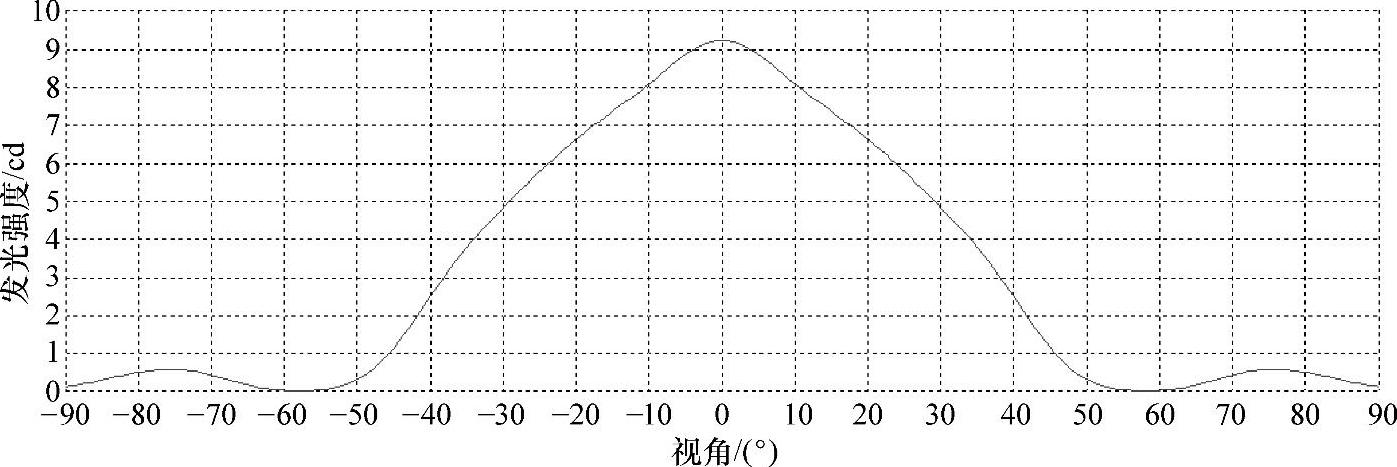
图5-11 加自由曲面透镜时的LED发光强度分布
以用式（5-1）来拟合，拟合的范围在-60°～60°之间，-60°～60°之间的发光强度占总发光强度的96.5%，这个范围之外的那部分发光强度基本可以忽略不计。由式（5-2）可以计算m=4.82。为了比较拟合的精确程度，可以将拟合的发光强度分布与原始的发光强度分布曲线放在同一张图上，如图5-12所示。可见加了自由曲面透镜后的发光强度分布可以拟合成m=4.82的朗伯分布，是一个非完美朗伯发光强度分布。
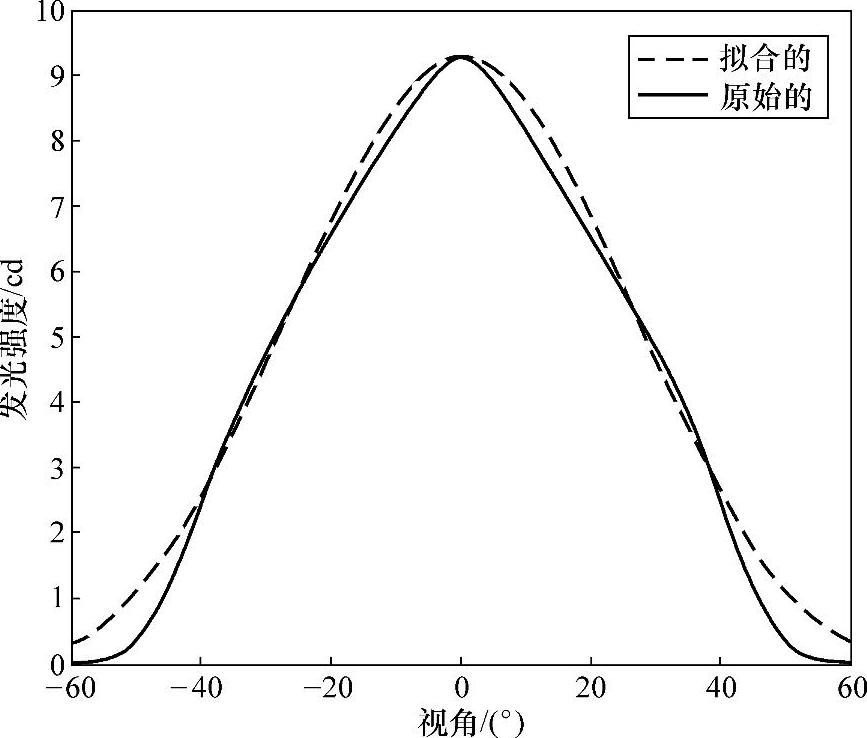
图5-12 圆形阵列中使用的LED的发光强度分布和拟合之后的发光强度分布
为了评价拟合的准确程度，使用归一化的互相关系数（NCC）作为评价的指标。NCC表示如下：
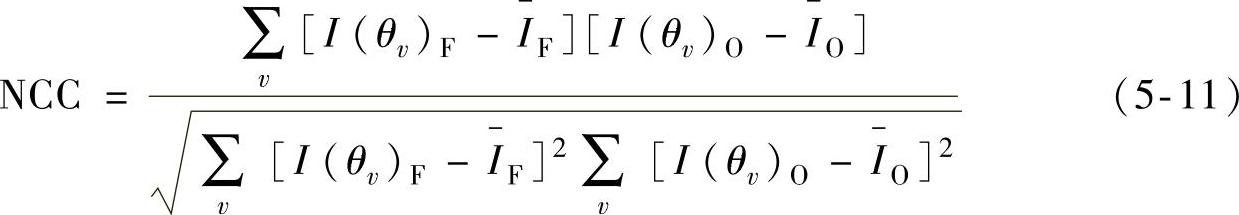
式中，IF和IO分别为拟合发光强度值和原始发光强度值；θv是第v个采样角；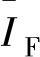
和
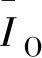是拟合发光强度在所有采样角的平均值和原始发光强度的平均值。NCC计算结果为99.5%。很明显拟合的曲线非常接近于原始的曲线。本案例中的LED的发光强度分布为
I（θ）=I0cosmθ（m=4.82） （5-12）
由非完美朗伯分布的LED构成的圆形阵列的优化与案例1的优化方法基本类似，这次使用的评价函数为式（5-5）。优化圆形LED阵列时所设置的初始条件如表5-1所示。在优化过程中目标函数的变化值（COFV）首先满足了停止条件。通过优化，最佳的圆形LED阵列半径为R=34.5mm。对应于这个最佳半径的圆形LED阵列，在目标面上产生了均匀的辐照度分布。图5-13是这个最佳的圆形LED阵列产生的辐照度分布和轮廓。
表5-1 优化圆形LED阵列的初始条件
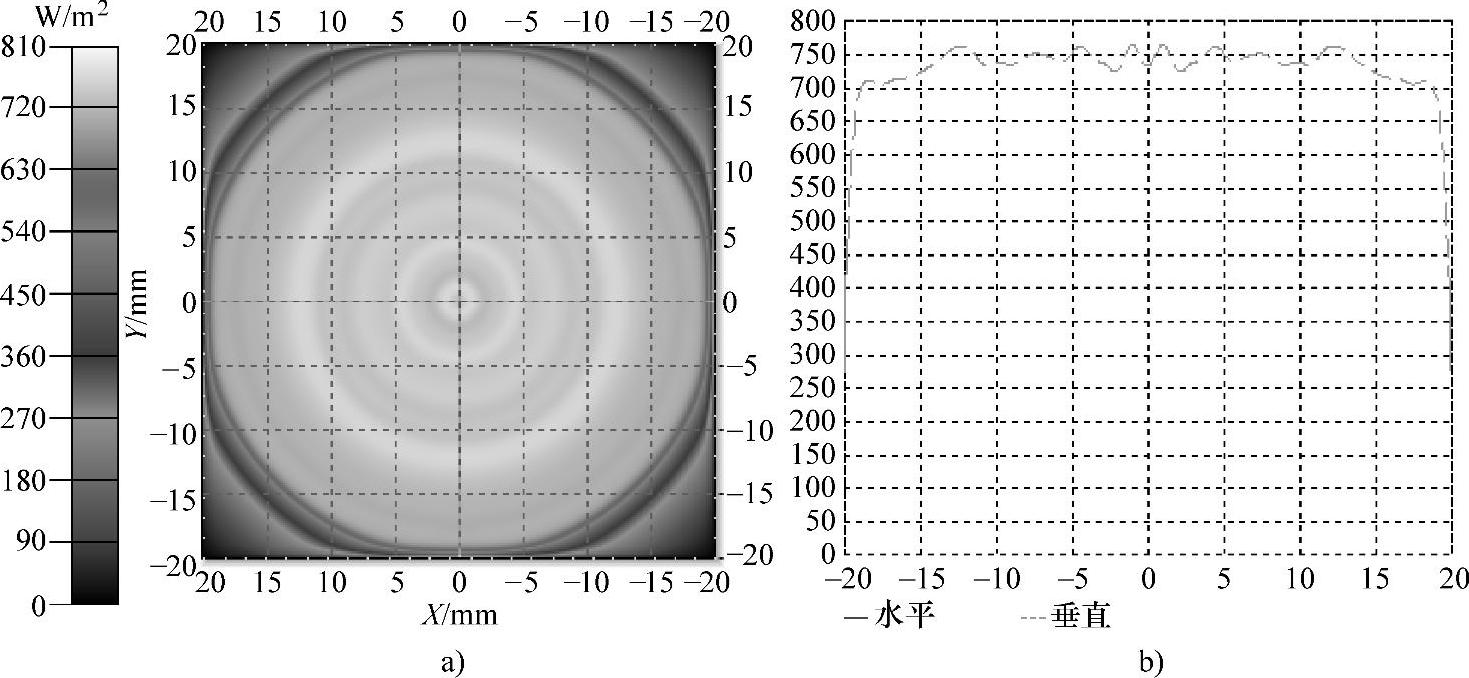
图5-13 优化之后的圆形阵列产生的辐照度分布和轮廓
a）辐照度分布 b）辐照度轮廓
案例3：完美朗伯分布的LED构成的矩形（或方形）LED阵列
本案例将讨论矩形（或方形）LED阵列的优化设计问题。假设要设计一个M×N（M和N为偶数）矩形LED阵列，相邻的两个LED之间的距离都设定为相等，因此这个阵列相邻LED之间的距离的改变就会影响目标面上的辐照度均匀度，因此优化这种阵列就是优化相邻LED之间的最佳距离。在优化过程中构建评价函数式（5-6）是必要的，构建评价函数需要获得辐照度分布的计算公式。为了推导矩形阵列在目标面上的辐照度分布表达式，以一个4×4方形LED阵列（见图5-14）为例子建立一个坐标系，相邻两个LED之间的距离为d。M×N（M和N为偶数）矩形LED阵列坐标系与4×4方形LED阵列基本类似。建立这样的坐标系后，很容易将每个LED的坐标用间距d表示出来：
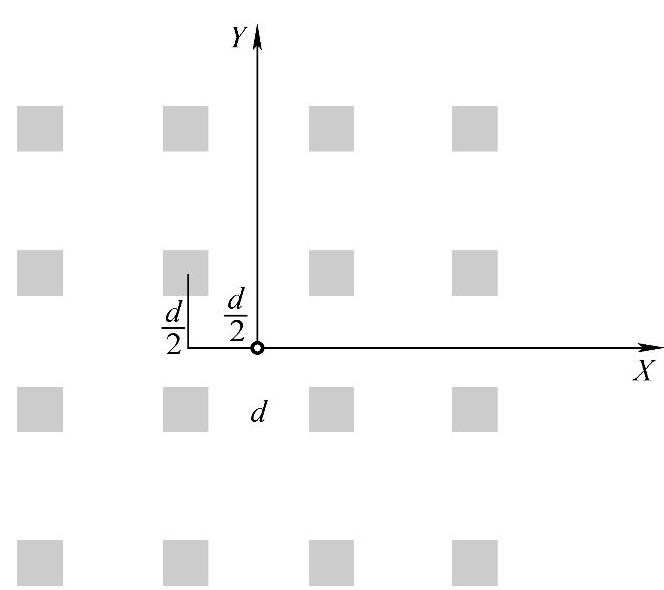
图5-14 4×4方形LED阵列示意图
根据上面的坐标计算公式，可以将4×4方形LED阵列中每个LED的坐标位置表示出来，如图5-15所示。
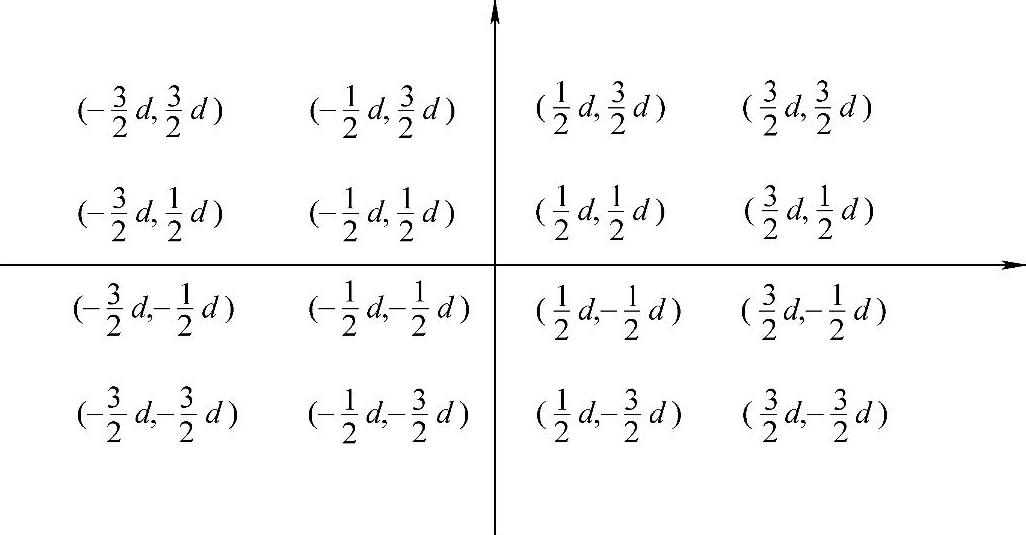
图5-15 4×4方形LED阵列排布的坐标图(www.xing528.com)
根据式（5-4）和式（5-13）可以得到这种M×N（M和N为偶数）矩形LED阵列辐照度分布计算式为
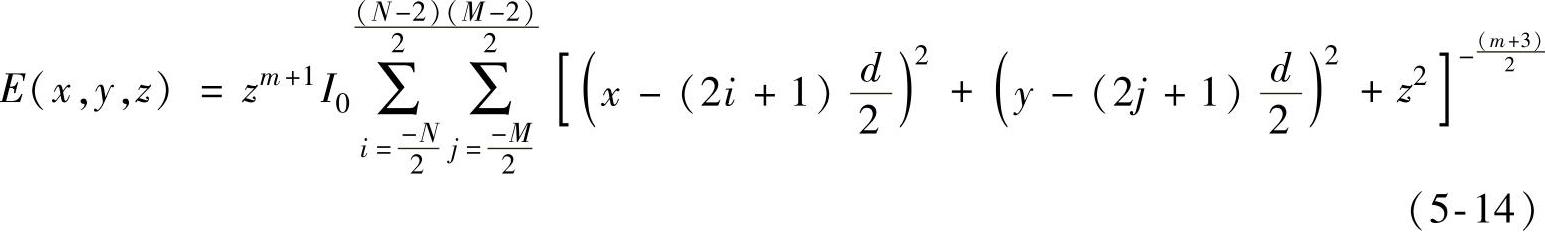
根据式（5-6）构建评价函数，评价函数中需要优化的变量就是相邻LED之间的距离。利用模拟退火算法优化相邻LED之间的距离，优化结果为d=12.79mm。优化后的4×4方形LED阵列如图5-16所示，这个阵列在目标面上产生的辐照度分布和轮廓如图5-17所示，均匀度为96%。
接下来讨论一下M×N（M和N为奇数）的LED阵列的坐标建立及辐照度分布计算。以一个5×5方形LED阵列为例建立坐标系如图5-18所示，LED的坐标为
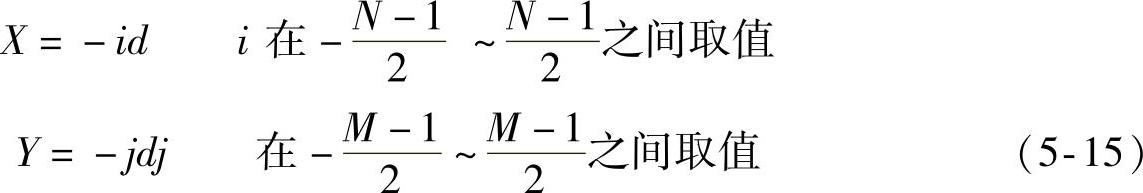
根据式（5-4）和式（5-15）可以推导出该阵列的辐照度分布计算式为
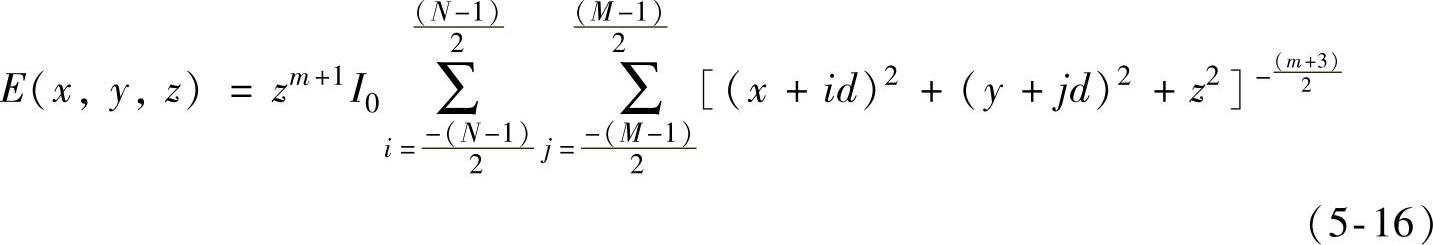
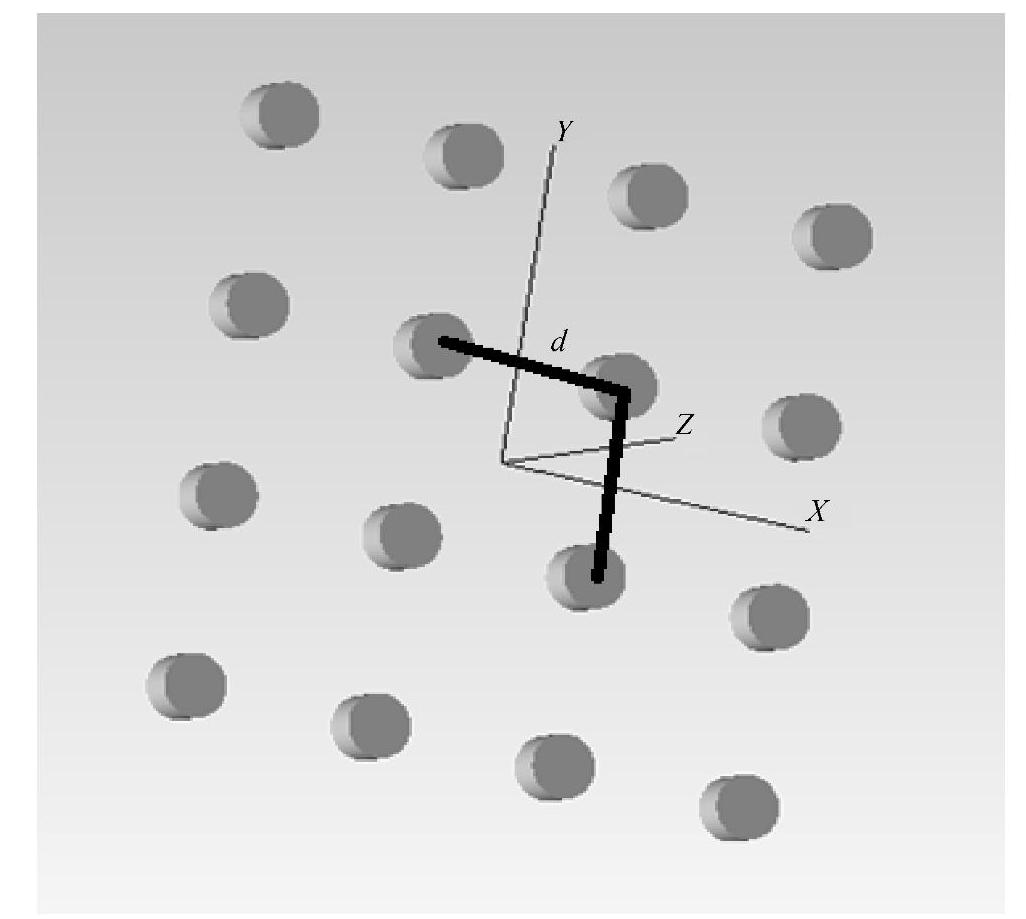
图5-16 优化后的4×4方形LED阵列
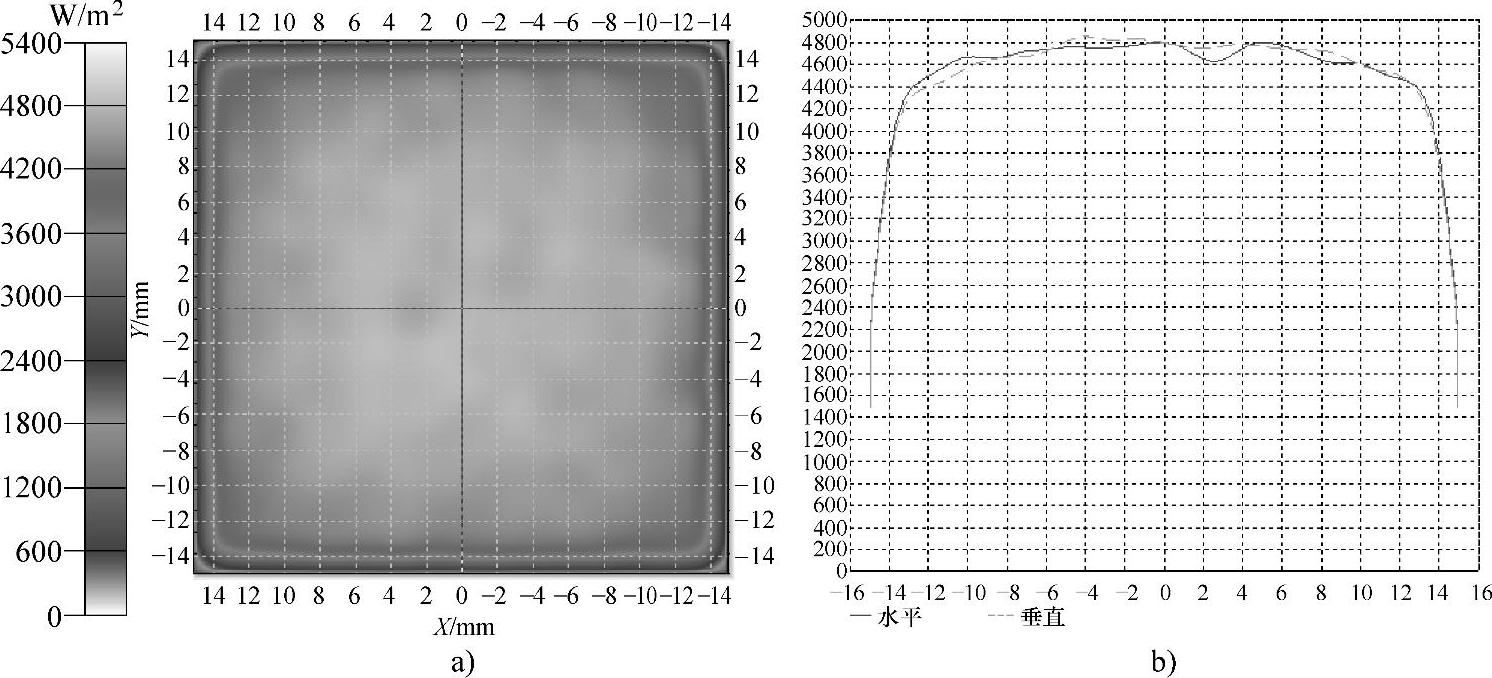
图5-17 4×4方形LED阵列排布的辐照度分布和轮廓
a）辐照度分布 b）辐照度轮廓
从4×4阵列和5×5阵列可以看出，当某一行或某一列LED的颗数为奇数或偶数时，LED阵列的坐标建立有一定的差异性。接下来优化设计一个4×5的矩形LED阵列，这个阵列每一行LED的颗数为奇数个，每一列LED的颗数为偶数个。在排布中，由于X轴方向和Y轴方向的颗数不同，可能会出现不同的间隔，我们将X轴方向的间距定义为dx，Y轴方向的间距定义为dy，LED的坐标为
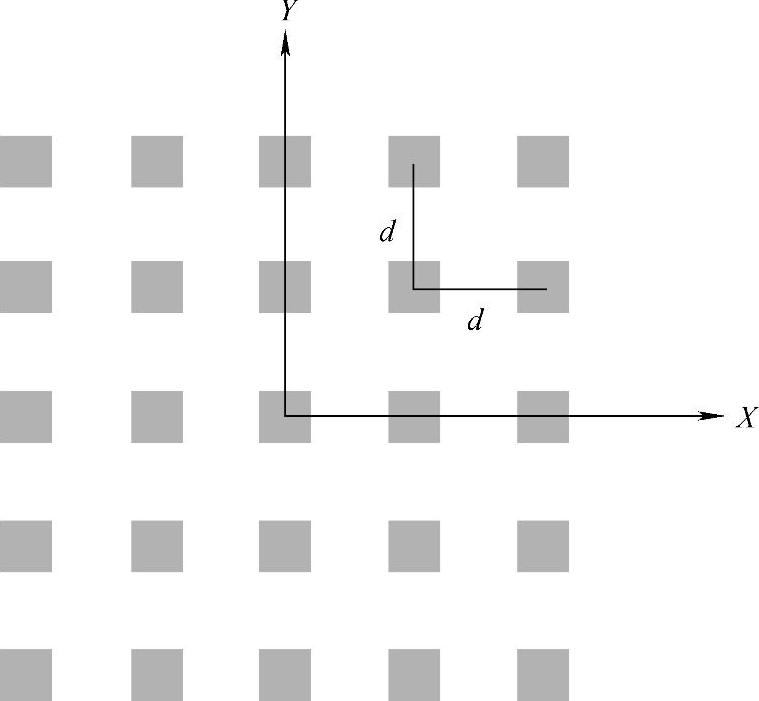
图5-18 5×5方形LED阵列示意图
X=-idxi在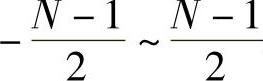
之间取值，N是奇数，为X轴方向的LED颗数
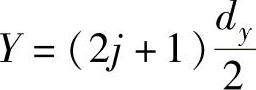j取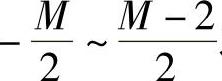
之间的整数，M是偶数，为Y轴方向的LED颗数 （5-17）
LED的坐标如图5-19所示，每颗LED的坐标都可以用dx和dy来表示。根据式（5-4）和式（5-17）可以写出该阵列在目标面上的辐照度表达式
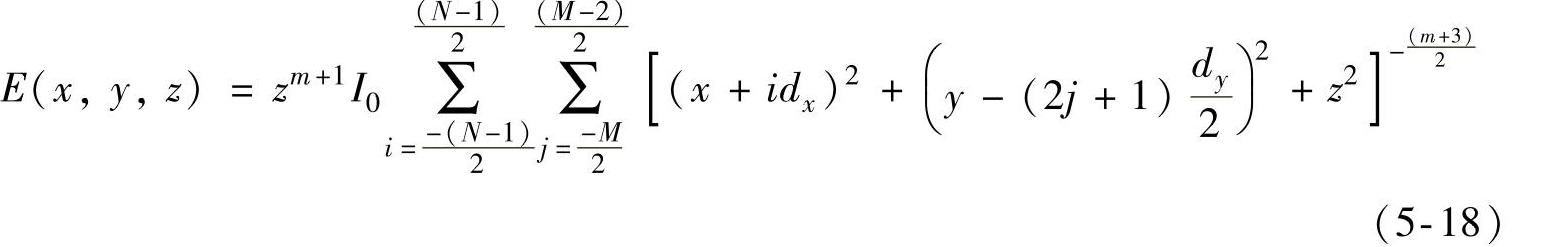
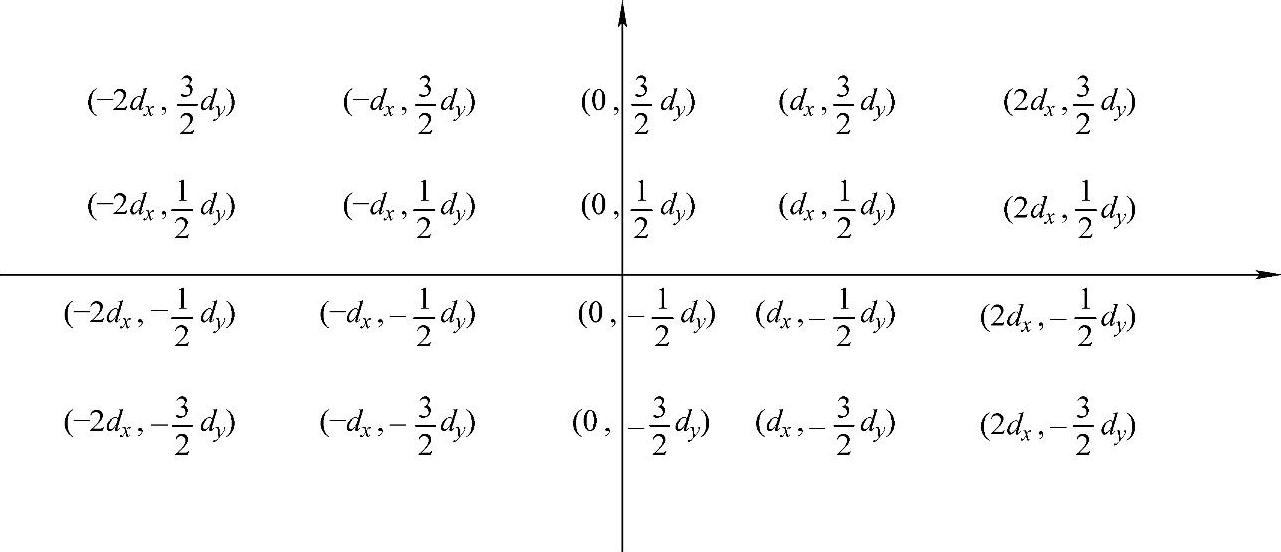
图5-19 4×5矩形LED阵列排布的坐标图
仍然使用式（5-6）作为评价函数。这个优化的阵列中有两个要优化的变量dx，dy。通过模拟退火算法可以得到最佳横向和纵向间距dx=11.54，dy=12.99。优化后的LED阵列分布如图5-20所示，图5-21为优化后的LED阵列在目标面上产生的辐照度分布，我们可以看出辐照度分布很均匀，均匀度计算结果为95%。
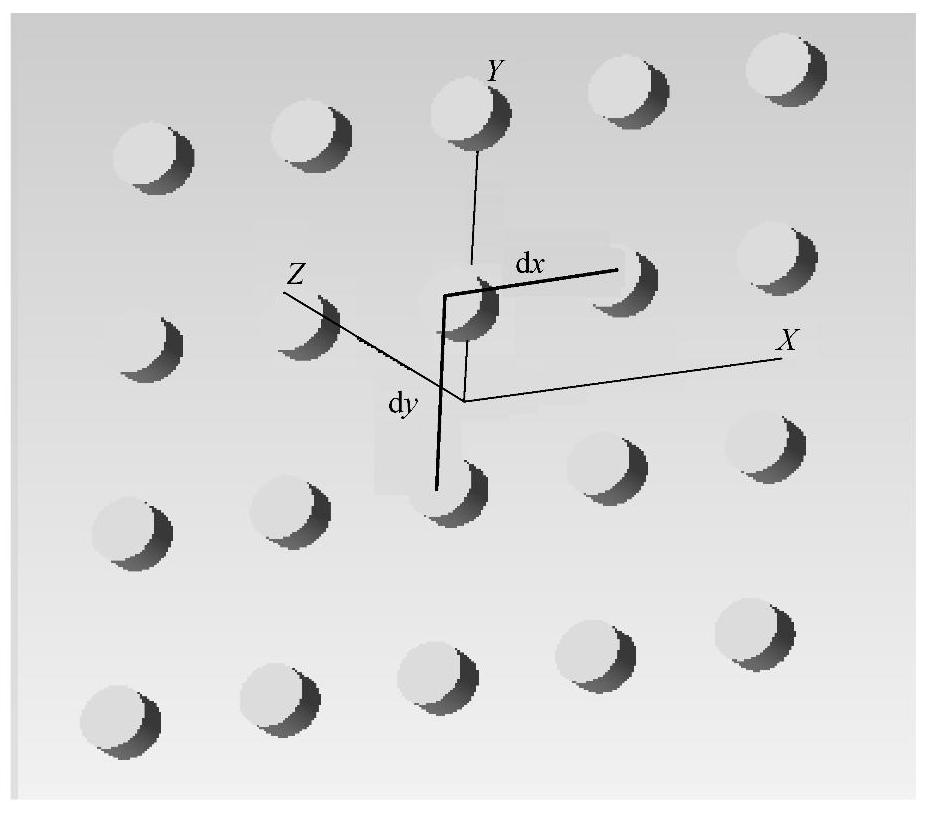
图5-20 4×5矩形LED阵列排布的效果图
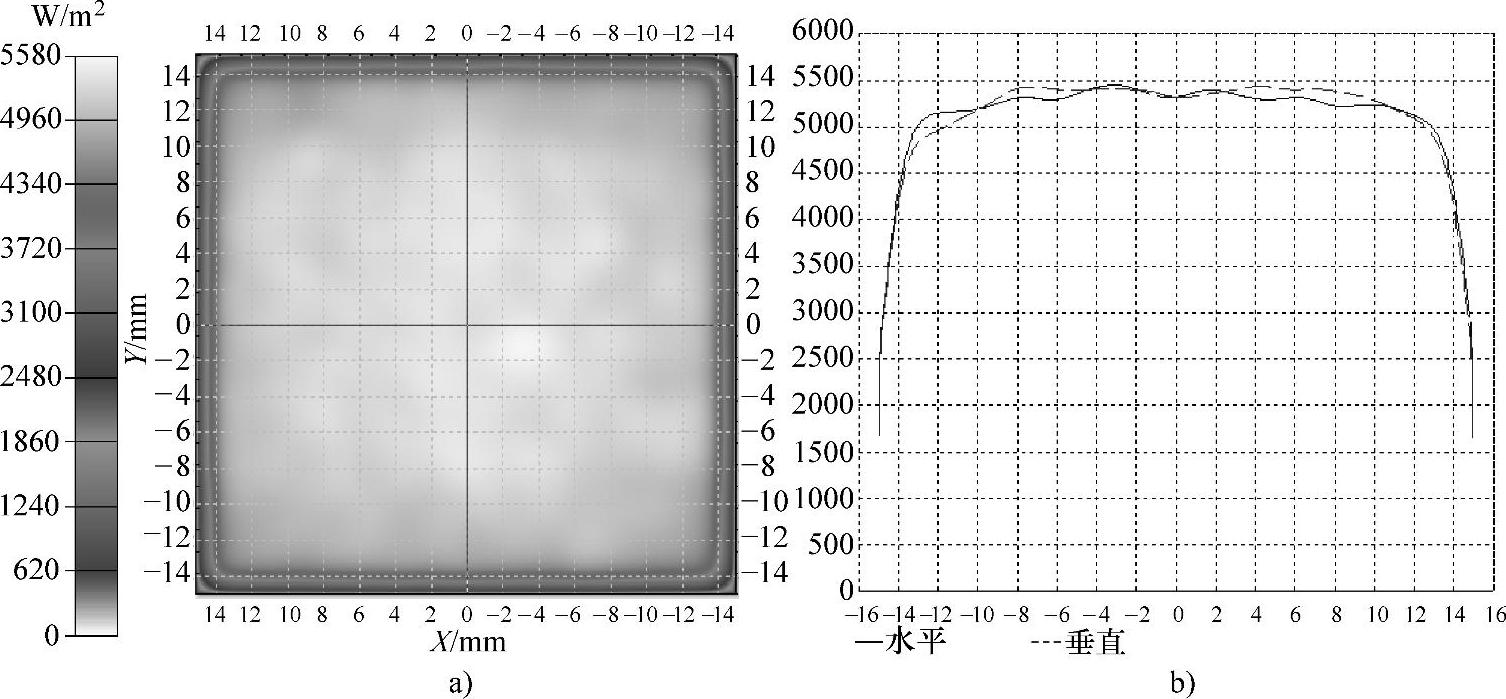
图5-21 优化后的4×5矩形LED阵列产生的辐照度分布和轮廓
a）辐照度分布 b）辐照度轮廓
案例4：复杂发光强度分布的LED形成的不规则阵列优化设计
为了证实这种方法的强大功能，这里优化一个复杂的LED阵列，该阵列是一个不规则的LED阵列，因此优化的变量非常多。在这个阵列中每颗LED有特殊的发光强度分布如图5-22所示。这种特殊发光强度是由于应用了一个特殊的透镜在LED后面而产生的。这个特殊的透镜是这样形成的，在一个平板上挖一个圆锥形的腔，如图5-23所示。其中图5-23a和b是这个透镜的二维和三维轮廓图。
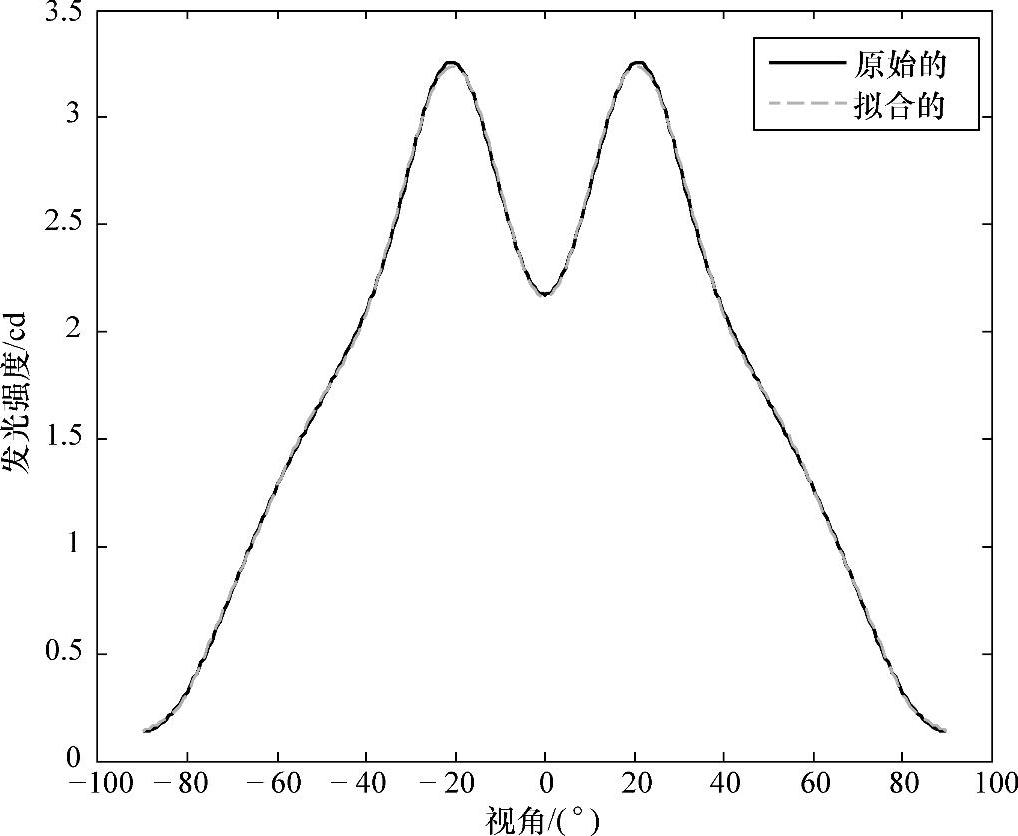
图5-22 加了特殊透镜之后的LED的发光强度分布
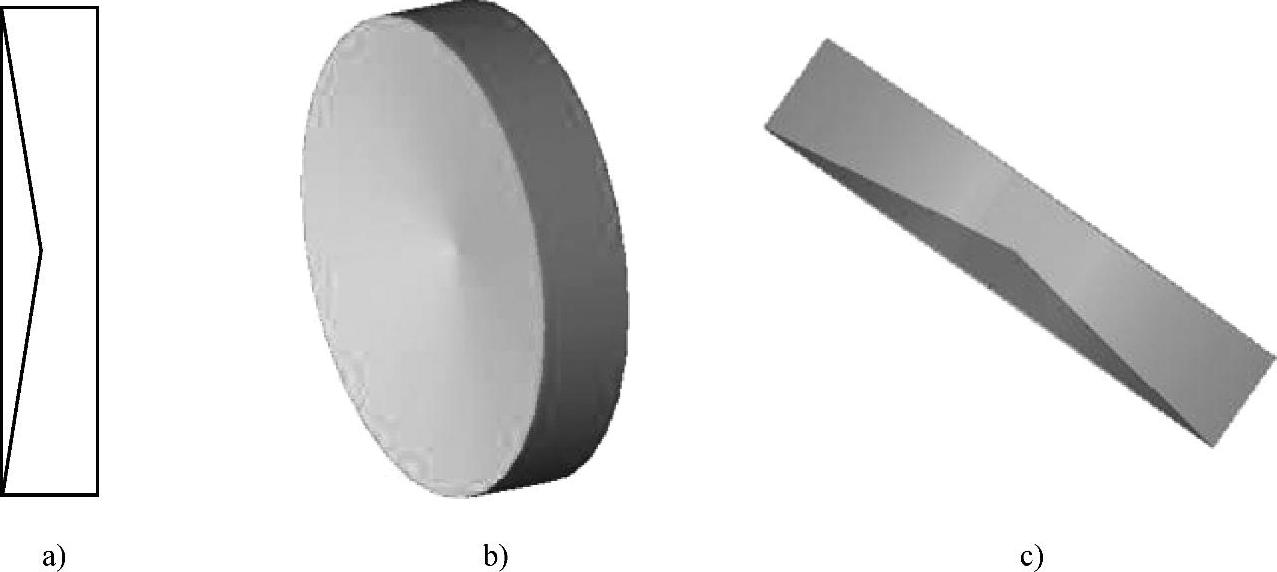
图5-23 特殊透镜的二维和三维轮廓图
从图5-22可以看出这个发光强度分布不是朗伯分布，因此无法用式（5-1）准确地拟合出来，拟合这个发光强度分布使用了关于cosθ的多项式如下：
I（θ）=a8cos8θ+a7cos7θ+…+a1cosθ+a0 （5-19）
式中，a8，a7，…，a0是多项式的拟合系数。在图5-22中，点画线代表了通过式（5-19）拟合出来的发光强度分布曲线。我们也计算了拟合曲线和原始发光强度分布曲线的NCC为99.99%。这表明了拟合的精度非常高。使用这个目前的发光强度表达式，目标面上的辐照度表达式为
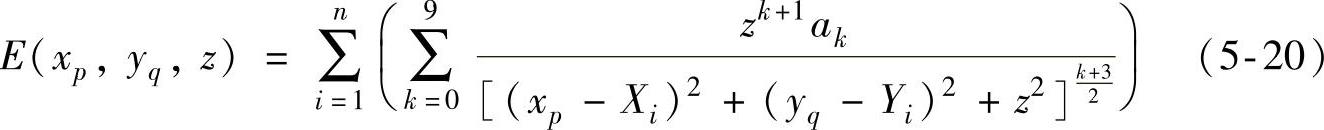
有了辐照度表达函数，可以使用相同的方法优化阵列。在这个阵列里，有4颗相同的LED，其发光强度分布如图5-24中的实线所示，其他3颗LED有相同的发光强度分布，如图中点画线所示，点画线代表的发光强度是实线代表的发光强度的1.5倍。这个阵列并没有约束其具体的排布形状，因此每颗LED的位置坐标都要作为优化的变量，这样7颗LED就有14个变量了。优化过程中使用的初始条件如表5-2所示，使用的评价函数为式（5-5），当评价函数的值达到了0.083，优化就停止下来了。经过优化，LED阵列排列如图5-25所示。图5-25中的菱形和圆形分别代表发光强度为实线和点画线的LED。图5-26为优化后的LED阵列在目标面上产生的辐照度分布和轮廓。这个均匀度的计算结果为87%。
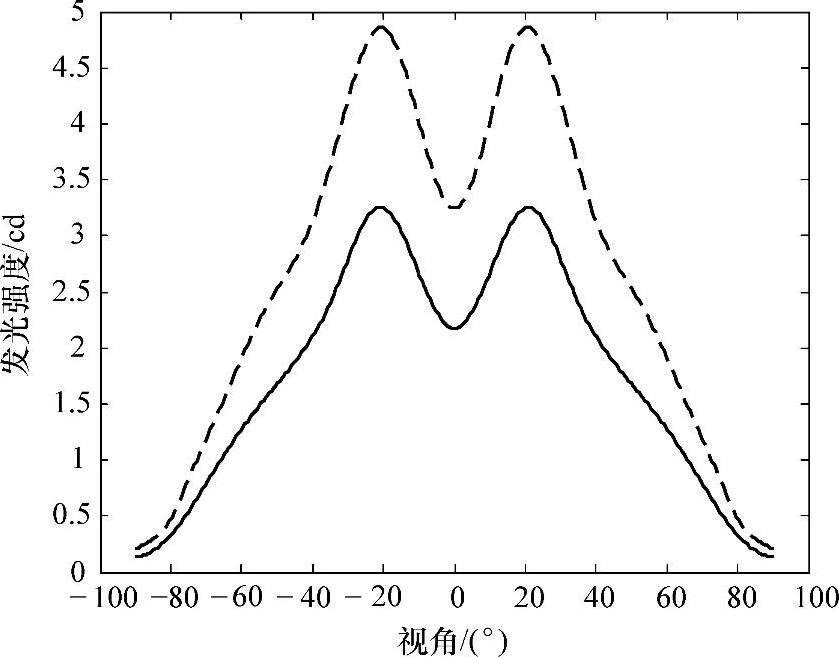
图5-24 第三个阵列中两种类型LED的发光强度分布曲线
表5-2 优化不规则LED阵列的初始条件
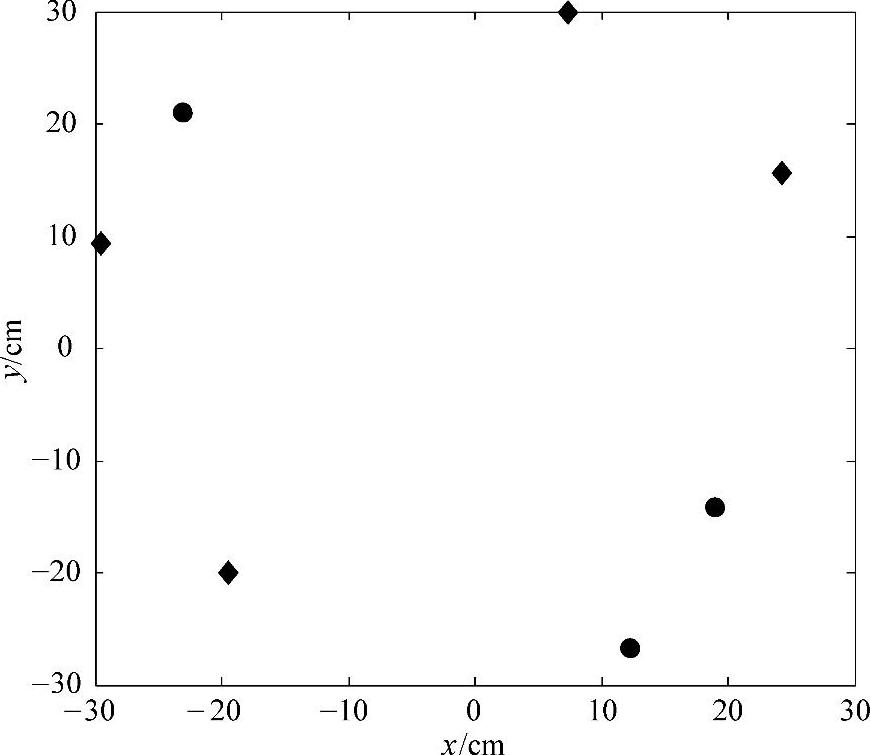
图5-25 不规则阵列优化后的排布图
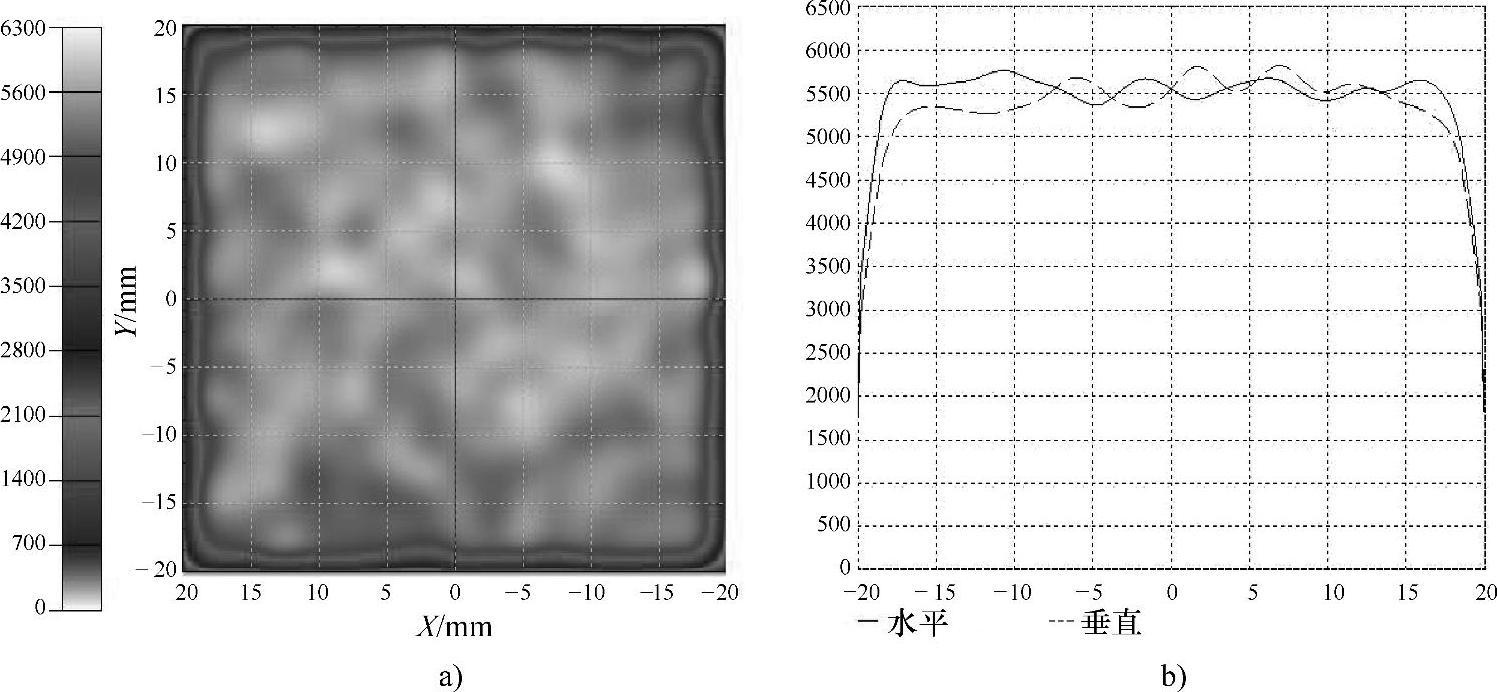
图5-26 不规则阵列优化后在目标面上产生的辐照度分布和轮廓
a）辐照度分布 b）辐照度轮廓
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
