模拟退火算法的设计与优化

模拟退火是一种全局优化算法，可以用来优化多变量目标函数的最小值。模拟退火，就像其名字所言，源于金属中的退火技术，整个过程包括了加热和控制物体冷却过程，使物体的缺陷达到了最小。在一个退火过程中，金属被加热到高温，变成无序状态。然后金属的温度逐渐下降，这样的过程在每一时刻都可以看作是一个热动力平衡的过程。当制冷过程继续，金属结构变得有序，最终结晶，这时候处于最低的能量状态。如果制冷过程比较长，冷却后的物体会变得非常完美。20世纪80年代Kirkpatrick和Cerny发现退火的物理过程和优化问题有很多相似性：①优化问题的当前解对应于热力学系统的当前的能量状态；②优化问题的目标函数对应于热力学系统的能量方程；③全局最小值对应于基态。

在这部分我们将讨论如何应用模拟退火算法来优化LED阵列。模拟退火作为一种全局优化的算法其实施流程如下。

1.初始化

1）构建目标函数如式（5-6）所示，目标函数可以反映LED阵列在照明目标面上的辐照度均匀度。

2）向量s作为一个初始解，包含了2n元素，这表示了n个LED坐标。

3）选择一个初始温度T=2000。

4）定义一个温度递减函数T_h+1=（0.95）hT_h，h是迭代次数，可以用来表示温度减少的数量。

5）设置迭代计数器和每个固定温度下的最大迭代计数次数。

2.迭代过程

1）设置h=0。

2）设置IT=0。

IT=IT+1。(www.xing528.com)

3）随机产生一组新的解s₁。如果f（s₁）＜f（s），这组新解被接受，这就意味着s=s₁。否则在[0，1]范围内均匀地产生一个随机数w。

如果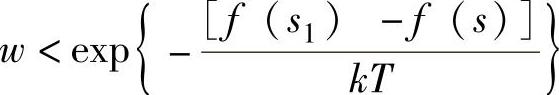，那么s=s₁。其中k是玻尔兹曼常数，T是当前的温度。

4）如果IT＜L，程序将返回到IT=IT+1。

5）如果终止条件满足，将返回到步骤3。

6）h=h+1。

7）按这个变化规律T_h+1=（0.95）hT_h更新温度，程序将会返回到步骤2中2）。

3.停止

4.输出最好值

从步骤2中3）可以看出，这个算法允许接收比当前解更糟糕的解。这将避免优化过程陷入局部最小值。当前的温度决定多大的概率来接受比当前解更糟糕的解。温度越低接受这种不利解的可能性越低。选择足够高的初始温度有利于达到全局最小值。当满足下列条件之一时，算法会终止：

1）目标函数小于预定函数的值。

2）目标函数的变化值小于预设的变化值。