基于多参数调整的反馈优化方法

在反馈优化过程中根据实际辐照度与预期辐照度的偏差可以调整目标面网格单元的大小，可以调整光源立体角大小，也可以同时调整目标面网格和光源立体角大小。下面就这几种情况分别进行讨论。

1.基于目标面网格调整的反馈优化

如果反馈优化过程中立体角的划分保持不变，始终保持初始透镜设计时划分好的立体角，想要调整实际辐照度与预期辐照度的偏差，就要通过调整目标面上的网格划分来实现。基于点光源设计初始透镜（旋转对称的），使用扩展光源进行光线追迹后，目标面上各区域的辐照度分布为E^（0）₁，E^（0）₂…E^（0）_i（0）…E^（0）_N如图4-3所示，下标数字表示目标面上的单元区域的编号，上标括号里的数字表示反馈的次数，如E^（m）_i表示第i单元区域经过m次反馈以后的辐照度分布。目标面上接收的光通量表示为

E^（m）₁S^（m）₁+E^（m）₂S^（m）₂+…+E^（m）_iS^（m）_i+…+E^（m）_NS^（m）_N=E_pS （4-2）

式中，E_p为目标面上的平均辐照度；S为目标面上的总面积。对式（4-2）进行化简可以得到

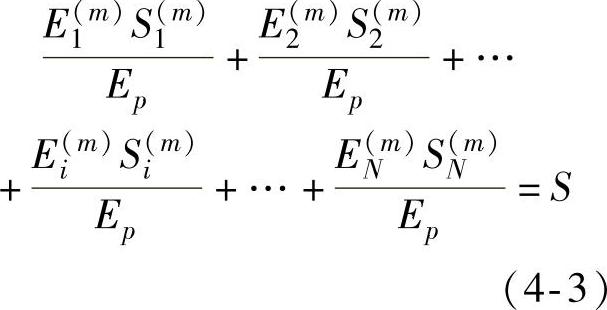
令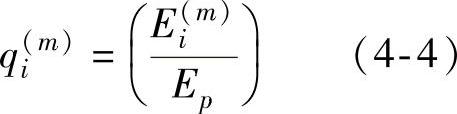

则 q^（m）₁S^（m）₁+q^（m）₂S^（m）₂+…+q^（m）_iS_i+…+q^（m）₁S^（m）_N=S （4-5）

令 S^（m+1）_i=q^（m）_iS^（m）_i （4-6）

根据式（4-6）可以看出目标面的网格面积在不断调整，调整的幅度主要取决于q^（m）_i，q^（m）_i是由式（4-4）决定的。每次调整目标面网格划分之后，重新构建透镜，追迹光线，如果目标面辐照度均匀性满足了要求，停止反馈优化。如果目标面辐照度均匀度不满足要求，继续反馈优化。这部分讨论的是光源每个立体角单元保持不变而调整目标面上的网格划分，所以根据式（4-6）可以近似为式（4-7）。

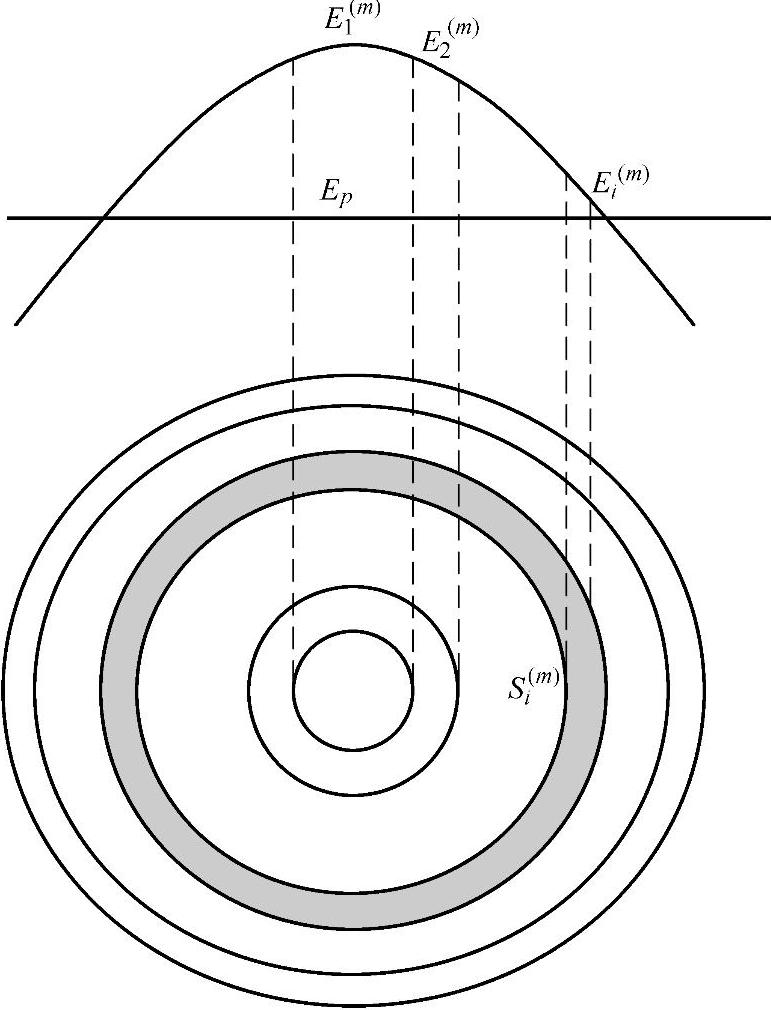
图4-3 目标面上的辐照度分布及光通量计算

令

联立式（4-7）和式（4-8）可以得到

E^（m+1）_i=k^（m）_iE^（m）_i （4-9）

式中，k^（m）_i为反馈系数，通过多次优化可以使实际辐照度逼近预期辐照度。

2.基于光通量划分调整的反馈优化

如果反馈优化过程中目标面上的网格划分保持不变，想要调整实际辐照度与预期辐照度的偏差可以调整光源的各立体角单元，从而改变了各立体角单元内的光通量。假设经过m次反馈以后，第i个单元的辐照度为E_i^（m），预期辐照度为E_p，则有

为了使E_i^（m）接近于E_p调整第i个立体角单元内的光通量如下：(www.xing528.com)

Φ_i^（m+1）=p_i^（m）Φ_i^（m） （4-11）

所以辐照度的分布理想值应为

E_i^（m+1）=p_i^（m）E_i^（m） （4-12）

因为对于扩展光源，调整立体角之后，调整后的光通量无法完全进入第i个面积元上，所以实际上E_i^（m+1）只能是接近p_i^（m）E_i^（m）。

令 k_i^（m）=p_i^（m） （4-13）

式中，k_i^（m）为反馈系数，通过多次优化可以使实际辐照度逼近预期辐照度。

3.同时调整目标网格与光源光通量单元

上面的两种情况都是只调整目标面或光源，实际上可以同时调整目标面和光源。假设经过m次反馈以后，第i个单元的辐照度为E_i^（m），预期辐照度为E_p，则有

目标面的第i个面积元和第i个立体角单元内的光通量都进行如下调整：

S_i^（m+1）=q_i^（m）·S_i^（m） （4-15）

Φ_i^（m+1）=p_i^（m）·Φ_i^（m） （4-16）

联立式（4-15）和式（4-16）可得

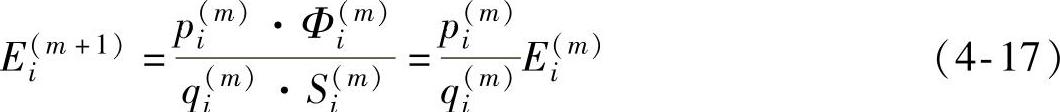
令 k_i^（m）=p_i^（m）/q_i^（m） （4-18）

p_i^（m）、q_i^（m）可以取值为

p_i^（m）=[k_i^（m）]^0.5 （4-19）

q_i^（m）=[k_i^（m）]^-0.5 （4-20）

将上述几种情况列表如表4-1所示，通过该表可以很好地比较这三种反馈情况的特点。