按等光通量划分光源：更合理的方案

将LED光源空间立体角分为M×N份，通过合理划分立体角，使每个立体角内有相同的光通量。这里先介绍一下立体角的计算，如图3-3所示，以坐标原点为球心构建一个半径为r的球面，球面中的阴影部分面积为

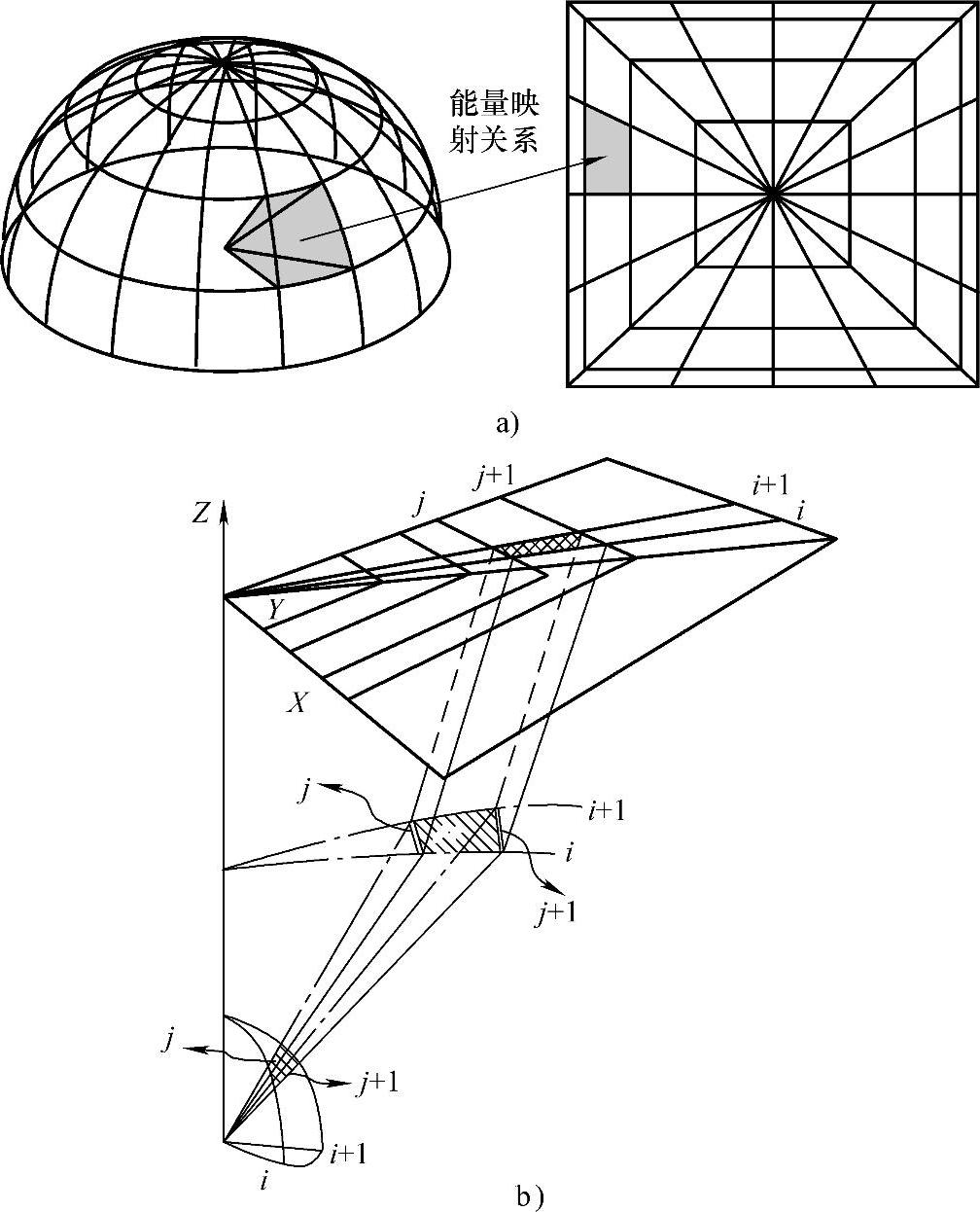
图3-2 使LED光源产生均匀辐照度分布的矩形光斑原理图

dS=rsinθdγrdθ=r²sinθdθdγ （3-1）

该阴影面积对球心O点所围成的立体角为

因为LED在目标面上要产生的光斑分布是矩形光斑，是一个1/4对称结构，所以设计的自由曲面透镜也必然是一个1/4对称的透镜。故在本设计中可先只考虑光源的1/4部分与矩形目标平面1/4部分之间的对应关系，之后再将所设计部分进行镜像对称即可。因此将光源按立体角进行等能量划分时只需要考虑1/4光源部分如图3-4所示，将LED光源1/4部分的能量按立体角分为M×N份，沿着纬线方向将空间划分为M份，沿经线方向将空间再划分为N份，任意相邻两条纬线和任意相邻两条经线围成一定的面积，该面积对应区域与球心围成一个立体角（见图3-4阴影区域），合理控制立体角的大小，使每个立体角内的光通量相等。

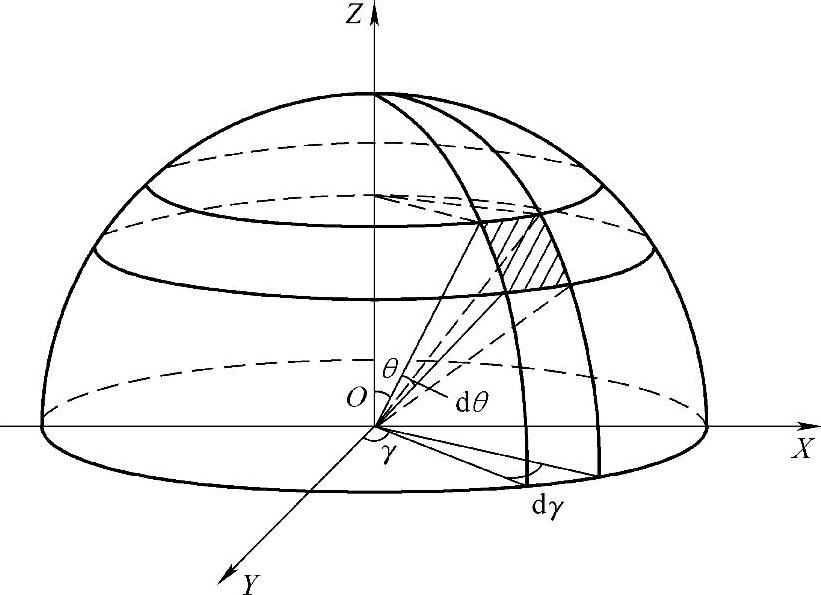
图3-3 空间立体角的计算原理图

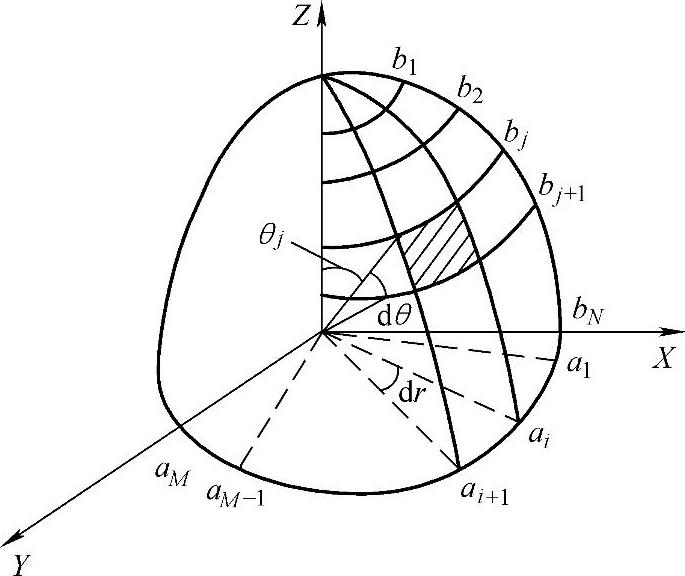
图3-4 LED光源按立体角进行等能量划分

该阴影区域所对应的立体角内的光通量可以由下式来计算：

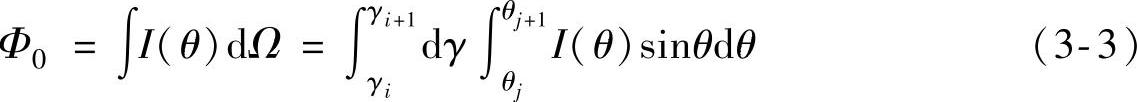(www.xing528.com)

式中，I（θ）为LED的发光强度分布，这里为完美朗伯光源，故I（θ）=I₀cosθ。

LED光源的总光通量（1/4部分）Φ_t为

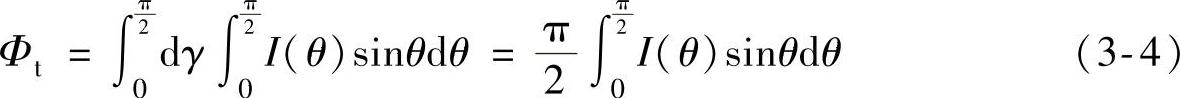
沿着纬线方向将空间按等角间隔分为M份，即相邻经线之间的角间隔为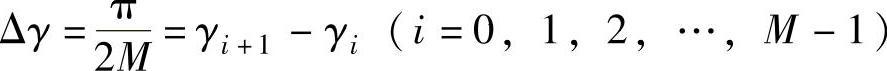，沿经线方向将其划分为N份，经线上任一个分割点与球心之间的连线可以作为一条采样光线，该采样光线与Z方向的夹角θ_j需要通过计算来求得。由于LED光源能量被等分为M×N份，每个立体角内的光通量为

联立式（3-3）、式（3-4）和式（3-5）可以得到

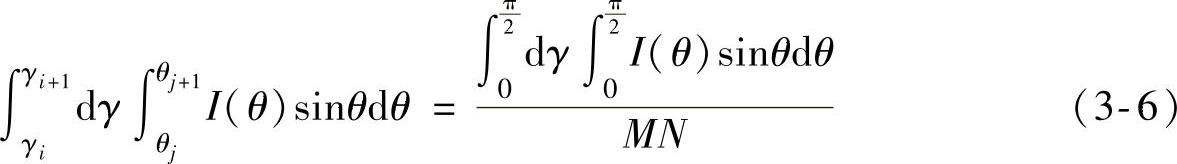
进一步化简可以得到

由式（3-7）可计算得到每一条采样光线与Z方向的夹角θ_j。这样将LED光源按等光通量划分为M×N份。将光源按等光通量划分以后，每一个分割点的坐标都可知，如第i条经线与第j条纬线的交点坐标为（sinθ_jcosγ_i，sinθ_jsinγ_i，cosθ_j）。

这样可以连接球心O点与每个分割点作为采样光线，这些采样光线可以用单位矢量（sinθ_jcosγ_ii，sinθ_jsinγ_ij，cosθ_jk）来表示。