精密冲裁的变形模式及原因解析

根据对精密冲裁塑性变形过程的测试、观察和分析，提出了精密冲裁的变形模式，如图2-3-5所示。对精密冲裁过程材料的变形和发展过程作如下的描绘，图2-3-5a表示精密冲裁开始时的状况，图2-3-5b表示冲裁凸模进入材料一定深度x时的情况。

图2-3-5 精密冲裁变形区域及变形过程

1—压边圈 2—凸模 3—凹模 4—反压板 5—工件 Ⅰ、Ⅱ—塑性变形区 Ⅲ—塑性变形影响区 Ⅳ—弹性变形区

图2-3-5中A、占二点分别表示凸模和凹模的刃口，AB连线将间隙区分为Ⅰ、Ⅱ两个部分，塑性变形主要集中在间隙区，Ⅰ、Ⅱ为塑性变形区，间隙两侧为刚性平移的传力区，它分为两部分，即靠近Ⅰ、Ⅱ区的塑性变形影响区Ⅲ和弹性变形区Ⅳ。精密冲裁的塑性变形始终在以AB为对角线的矩形范围中进行，例如当凸模进人材料一定深度茹时，A点以上的部分和B点以下的部分均已完成变形，精密冲裁继续进行时，塑性变形将在缩短了的AB为对角线的矩形中进行，如图2-3-5b所示。

凸凹模刃口连线AB还将塑性变形区分成I、Ⅱ两个区间，在精密冲裁过程中I区间的材料将被凸模逐渐挤压到条料上，Ⅱ区间的材料将被凹模逐渐挤压到工件上。

随着精密冲裁过程的进行．AB距离和矩形变形区逐渐缩小，一部分材料将转移到A、B以外的已变形区，当AB距离达最小值时，材料全部转移，精密冲裁过程完毕。

实际生产中，精密冲裁件出现的倒锥现象，即凸模侧大凹模侧小，就是以上所Ⅰ述I区的材料随凸模刃口A向下转移到条料（或孔），Ⅱ区的材料随凹模刃口日向上转移到工件的结果。

变形区材料的变形程度随变形区的逐渐缩小而增加，因此最先转移到已变形区的材料变形程度最低，然后逐渐增加．这些变形程度不同的材料逐次转移到工件表面。这就是实际生产中精密冲裁件剪切面从凹模侧到凸模侧变形程度逐渐增加的原因。

-2-3—5中还给出了精密冲裁塑性变形区的变形力学简图，其中主应力简图为三向压应力状态，主应变简图为平面应变状态₁=-ε₂，ε_，s3=0，即是将精密冲裁过程视为纯剪切的变形过程。实际生产中，精密冲裁凸模和凹模的间隙过小时，有时在精密冲裁剪切面上出现内凹的波纹，这是由于间隙过小时将使厚度方₁s．，因为ε₁+ε₂82=0，结果导致垂直工作表面的压应变增加，而出现内凹的现

六、精密冲裁变形区的应力

精密冲裁时作用于材料的外力和变形区的应力，如-2-3—6所示。

2-3-6 精密冲裁时作用于材料的外力及变形区承受的应力

1— 压边圈2 —凸模3 —凹模 4—反压板 5—工件

图中：

P_y——凸模作用于材料的冲压力；Py=P′_y+P″_y

p″_y——顶件反力

P′_y——冲裁力

P_v——V形齿内边作用于材料的力；

N——作用于材料的侧向力；

F_x：F_y——模具表面作用于材料的摩擦力。

1．变形区内任一点的应力张量

在变形区内任一点0取坐标系XYZ，在该处取一基元六面体，其上作用的应力如-2-3—6b所示δ_y。P_y系由0而引起的正δ_vx力δ_vy，Uvx_v，X分别由P，在x_方向Y量P_vx和l_vy方向的分量PH引δ_n正应力力Nc。为侧向力Ⅳδ_z起的正应力，吒为模具等对材料的约束作用而引起的正应力，剪应力由外摩擦力而引起。

O点的应力张量以Tσ表示

Tσ=Tσ′+T″σ

式中Tσ′——球形应力张量；

T″σ——应力偏量。(www.xing528.com)

球形应力张量系O点所受的静水压，它影响该点材料的塑性。

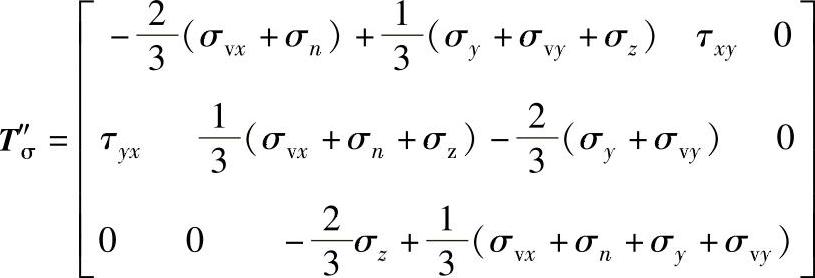
应力偏量T″σ包括一对剪应力τ_xy、τ_yx和由

构成的二对剪应力，应力偏量使材料在精密冲裁过程中产生塑性变形。

2.关于提高变形区静水压力的分析

精密冲裁时变形区的球形应力张量为

是该区所受的静水压力。而

因此从上式可以知道影响变形区静水压力的因素，从而找到提高静水压的途径：

（1）增大σ_yσ_y=σ′_y+σ″_y，σ′_y系冲裁力所引起的正应力，σ′_y在材料一定时为一定值，σ″_y系顶件反力P″_y所引起的正应力，因此增加σ_y只能通过增加σ″_y来实现，就是说增大顶件反力是提高精密冲裁变形区静水压的途径之一。

（2）增大σ_nσ_n为侧向力引起的正应力，它与凸凹模间隙及刃口的圆角密切相关，间隙偏大σ_n将降低，因此小间隙是实现精密冲裁的关键因素。当然采用小间隙的目的不仅是为了提高σ_n。在生产当中或在精密冲裁试模时，如果发现工件某局部出现撕裂采取措施仍不能克服时，可将相应部位的凹模刃口倒圆，借增加σ_n来提高静水压力，作为消除局部撕裂的一种办法。

（3）增大（σ_vx+σ_vy）因为显然增大（σ_vx+σ_vy）可通过增大P_v来实现，就是说增大压边力是提高精密冲裁变形区静水压力的途径之一。

（4）采用最佳压边圈齿形内角α当压边力一定时，还存在着压边圈齿形内角α取何值时（σ_vx+σ_vy）有最大值的问题。

由于σ_vx为P_vx引起的应力，σ_vy为P_vy引起的应力，所以（σ_vx+σ_vy）的极值问题，可以归结为求（P_vx+σ_vy）的极值问题。

由图2-3-6知

取极值：

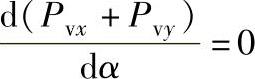
得P_v（cosα-sinα）+dP_v（cosα+sinα）=0

因压边力为一定，P_v为定值，dP_v=0故

以上结果表明，齿形内角α=45°时，（P_vx+P_vy）或（σ_vx+σ_vy）有极大值，此时精密冲裁变形区内材料所受的静水压力最大。

（5）关于σ_z的分析 从静水压力的关系式中知σ_z增加也可提高静水压力，但σ_z为模具等对材料约束而引起的应力，它取决于工件的轮廓，在工件轮廓内凹的部分σ_z值比较大，这些部分压边圈的齿形不必沿工件轮廓线分布，就能使变形区有足够大的静水压力，从而使精密冲裁过程获得完美的结果。