如前所述,混凝土纯扭构件在裂缝出现前,钢筋应力很小,且钢筋对开裂扭矩影响也不大。可以忽略钢筋的作用。

图6.3 矩形截面受扭构件
图6.3 所示为一在扭矩T 作用下的矩形截面受扭构件,扭矩使截面上产生扭剪应力τ。由于扭剪应力作用,在与构件轴线呈45°和135°角的方向上相应的产生了主拉应力σtp和主压应力σcp,并有
![]()
若混凝土为理想弹塑性材料,在弹性阶段,构件截面上的剪应力分布如图6.4 (a)所示。最大扭剪应力τmax及最大主应力,均发生在截面长边中点处。当最大扭剪应力值及最大主应力值到达混凝土抗拉强度值时,截面并未发生破坏,荷载还可少量增加,直到截面边缘的拉应变达到混凝土的极限拉应变值,截面上各点的应力全部到达混凝土的抗拉强度后,截面才开裂。此时,截面承受的扭矩称为开裂扭矩Tcr。如图6.4 (b)所示。
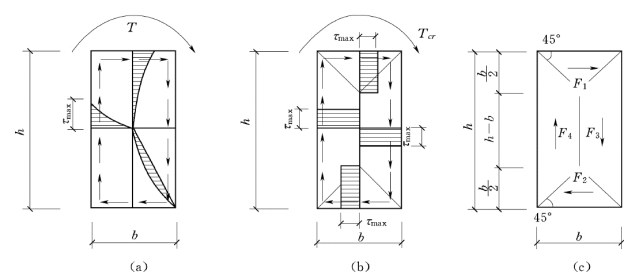
图6.4 扭剪应力分布图
根据塑性力学理论,可把截面上的扭剪应力划分成四个部分,如图6.4 (c)所示。计算各部分扭剪应力的合力及相应组成的力偶,其总和则为Tcr。如图6.5 所示,各部分剪应力合力对截面中心取矩,得:
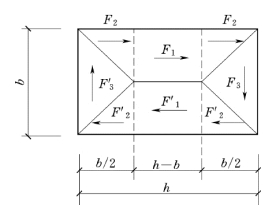
图6.5 塑性理论计算Tcr(https://www.xing528.com)
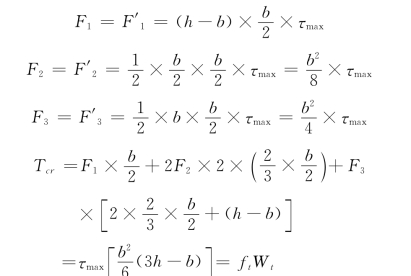
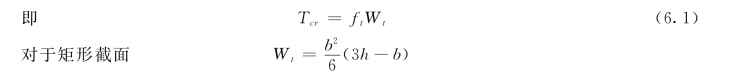
式中 Tcr——开裂扭矩;
Wt——受扭构件的截面受扭塑性抵抗矩;
b、h——矩形截面的短边和长边尺寸。
根据弹性力学理论,则当最大扭剪应力及最大主应力达到混凝土抗拉强度ft时,构件开裂,开裂扭矩则为:
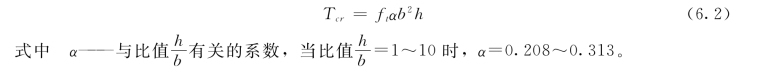
实际上,混凝土既非弹性材料又非理想的弹塑性材料,而是介于两者之间的弹塑性材料。试验表明,当按式 (6.1)计算Tcr时,计算值总比试验值高,而按式 (6.2)计算Tcr时,则计算值总比试验值低。为实用方便,开裂扭矩可近似采用理想弹塑性材料的应力分布图形进行计算,但混凝土抗拉强度要适当降低。试验表明,对高强度混凝土,其降低系数约为0.7,对低强度混凝土,降低系数接近0.8。
《混凝土结构设计规范》(GB50010—2002)取混凝土抗拉强度降低系数为0.7,故开裂扭矩计算公式为:
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




