结构的可靠度可用可靠概率pS来描述。可靠概率pS=1—pf,pf为失效概率。因此,要计算可靠概率pS,就应先计算失效概率pf。
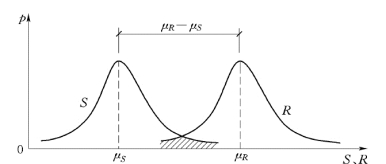
图3.2 S、R 的概率密度分布曲线
设构件的荷载效应S、结构抗力R 均为服从正态分布的随机变量且二者为线性关系。S、R 的平均值分别为μS、μR,标准差分别为σS、σR,S、R 的概率密度分布曲线如图3.2 所示。
按照结构设计要求,μR 应大于μS,从图3.2 中可看出,在大多数情况下构件的R 大于S,但由于离散性,在S、R 的概率密度曲线重叠区(阴影部分),仍有可能出现构件的R 小于S 的情况。所以,重叠区的大小反映了R 和S 间的概率关系,即结构的失效概率pf。
从结构安全角度可知,提高结构构件的抗力[4],减小R 和S 的离散程度[5],可以提高结构构件的可靠程度。所以,加大平均值之差μR—μS,减小标准差σS和σR可以使pf降低。
Z=R—S,Z 也是服从正态分布的随机变量,Z 的概率密度分布曲线如图3.3 所示。图中阴影部分表示出现Z<0 事件的概率,也就是构件的失效概率pf,可表示为:
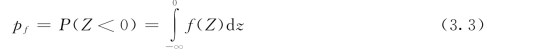
但是按式(3.3)计算失效概率pf比较麻烦,故改用一种可靠指标的计算方法。从图3.3 可看到,阴影部分的面积与μZ 和σZ的大小有关:增大μZ,曲线右移,阴影面积将减少;减小σZ,曲线变得高而窄,阴影面积也将减少。如果将曲线对称轴至纵轴的距离表示成σZ的倍数,即取μZ=βσZ,式中β大,则曲线右移,阴影面积将减少,失效概率pf小。所以,β和失效概率pf一样可作为衡量结构可靠度的一个指标,称为可靠指标。计算公式如式(3.4):
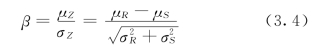

图3.3 可靠指标与失效概率关系示意图
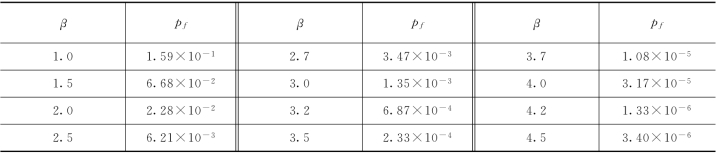
β与失效概率pf之间有一一对应关系,见表3.3。(https://www.xing528.com)
表3.3 可靠指标β与失效概率pf的对应关系
结构和结构构件的破坏类型分为延性破坏和脆性破坏两类。延性破坏有明显的预兆,可及时采取补救措施,所以目标可靠指标可定得稍低些。脆性破坏常常是突发性破坏,破坏前没有明显的预兆,所以目标可靠指标就应该定得高些。《建筑结构可靠度设计统一标准》(GB50068—2001)根据结构安全等级和破坏类型,在对代表性的构件进行可靠度分析的基础上,规定了按承载能力极限状态设计时的目标可靠指标β值,见表3.4。
表3.4 结构构件承载能力极限状态的目标可靠指标[β]

用可靠指标β进行结构设计和可靠度校核,可以较全面地考虑可靠度影响因素的客观变异性,使结构满足预期的可靠度要求。
【例3.1】 受恒载作用的钢筋混凝土梁,受弯承载力极限状态方程为Z =R—S =0,已知荷载效应(弯矩M)服从正态分布,且μM=13kN·m,δM=0.07;抗力R 假定为服从正态分布,且μR=20.80kN·m,δR=0.094;求此梁的可靠指标β。
【解】 1.参数计算
已知μR=20.80kN·m;δR=0.094,σR=δRμR=0.094×20.80=1.955kN·m
μs=μM=13kN·m,σS=σM=δMμM=0.07×13=0.91kN·m
2.求可靠指标β
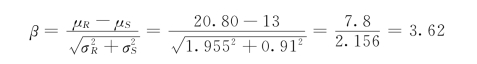
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




