如何提高掩密通信的信道容量？

掩密信道的容量，其定义还没有统一。传统信道容量也是一样，只有笼统的、抽象的定义：通过信道可靠传输的最大信息速率。也有针对不同信道，给出具体信道容量计算公式的定义。对传统信道容量而言，不管哪种定义，均离不开作为通信信息载体的“信道”、离不开作为量化指标“最大传输速率”。

对于基于信息隐匿的掩密通信而言，信道不再是常规通信中的通信信道，而是信息隐匿（Information Hiding）中的“掩护媒体”（Cover media），如图像、声音、各种格式的文档等。这样的信道称之为“掩密信道”（Covert Channel）。国际上从1999年已开始进行关于其容量的研究。

传统“信道容量”的定义是基于“可靠传输”的思想来定义的，而根据掩密通信的特点，掩密通信容量的定义应基于“可靠掩密”或“可靠隐蔽”的思想来定义。

1.掩密信道的基本模型

美国麻省理工学院（MIT）媒体实验室在信息隐匿系统的分析中遇到3个相互矛盾的问题（隐匿信息量、隐匿信息鲁棒性和隐匿信息的隐蔽性）时，从信息论角度提出了一个简单的基于静止图像的信息掩密通信系统信道模型。其中，将承载秘密信息的原始掩护图像视为一个近似连续的二维带限信道，并具有较大的平均噪声能量，而秘密信息则被视为通过这一信道传递的信号。基于这一模型，任何一种用于连续信道通信手段——调制技术均是一种潜在的信息隐匿技术，这为数字水印算法的设计开辟了一个思路。根据Nyquist理论和香农（Shannon）定理以高斯噪声信道为基本信道模型，可以计算出信道容量以及在给定带宽W条件下，为了达到信道容量C所需S/N的下限。即

由式（4-13）可以看出，在低信噪比的条件下，该水印信道容量与系统信噪比成正比。可以引用通信系统中的概念和方法来分析这一模型，如信道容量、信噪比、干扰容限等。但该简单模型具有许多局限性，如其中假设信息仅在空间域进行叠加。

RamKumar等人以上述模型为基础，对其进行了改进，设计了加噪条件下的信息掩密信道模型，并对其进行了相应的系统分析。如图4-9a所示。在该系统中存在两个噪声源，I是有原始图像调制传输信息时引入的噪声，而P则是由于信号处理（包括有意和无意的处理操作，如压缩/解压缩）引入的噪声。S为通过该信道传输的隐匿信息。对于非盲的信息隐匿算法，则信道中仅存在信号处理噪声P。

图4-9 信息掩密信道模型图

图4-9b给出了一个简单加性噪声容量模型，X～[f_X（x），σ²_x]表示需要传输的信息；Z～[f_Z（2），σ²_z]表示信道加性噪声；Y～[f_Y（y），σ_y]表示信道输出端接收的信息。假设X、Z两者相互独立，由信息论中信道容量公式可得，该加性噪声信道的容量C为

其中I（X，Y）是X、Y的互信息量，这样对于一个给定的噪声统计特性和输入方差，通过选择一个适当分布的输入信息，可以得到输入Y时最大熵。通过一个等熵转换器将噪声信号转换成等熵的高斯分布信号，得到该掩密信道的容量公式：

式中，σ²_s为隐匿信息的能量；

σ²_ig为图像调制噪声；

σ_p²为信号处理噪声。

通过一系列假设简化了公式，在计算图像调制噪声时，假设图像是一个在0～255平均分布的函数，通过等熵计算转化为高斯分布函数，并计算出等熵方差。一个简单的例子，在“联合摄影专家组”（JPEG）压缩为50%质量时，信道容量仍为0.0022比特/像素，这意味着对于256像素×256像素的图像可以嵌入144bit，当信噪比降到22dB时仍可嵌入124bit。

该模型进一步完善了掩密信道模型，将图像调制和信号处理作为两个并行噪声干扰引入信道，通过等熵转换简化模型计算，并结合了几种变换编码模式计算信道噪声模型，对不同变换模式下的该信道容量进行了分析比较。

2.掩密信道容量的基本定义

国际上已有少数学者进行了基于信息隐匿的掩密通信的信道容量研究，但关于掩密信道容量的定义还没有统一。

现在把水印处理过程看成是通信，它包含两个主要的步骤：

1）水印嵌入（Watermark Embeding）。在这个过程中，水印被看成秘密信息，掩护图像被看成信道，称为水印信道（Water mark channel）；

2）水印恢复（Watermark Recovery）。在这个过程中，秘密信息从收到的掩护图像中提取出来。

定义4.1：在图像中能隐藏的最大信息比特数，称为水印信道的容量。

该定义虽然对图像作为掩护信而言的，对其他信息作为掩护信息也是成立的。指出了容量计算的重要性在于：在不管秘密信息如何被提取的情况下，能给出以图像作为掩护媒体的掩密通信中，一幅图像（信道）能够传输的秘密信息量的上界。在传统的通信系统中，信道容量依赖于信息信号的能量及信道的特性。相似地，图像水印信道的容量应该依赖水印（信息信号）的强度、图像的统计特性和水印的嵌入方式，后两种特征代表的是图像水印信道的特性。

基于盲提取信息隐匿技术对于给定的图像压缩方案定义了信息隐匿信道的容量，用定义4-2表述。

定义4-2：设I表示掩护图像，S表示嵌入到I中的秘密信息的比特流，I′表示含密图像，C表示某种压缩方案，I″表示I′经C压缩（如JPEG压缩）后的图像，用下式表示嵌入过程和压缩过程：

满足①I与I′视觉不可区分；②从I″中提取秘密信息S′与S的误差概率可以任意地小。即对于任意的事先给定的ε，使得

式中，P表示概率；

‖S′-S‖表示S′与S中相异的比特数。

则称S中的比特数为对于压缩方案C的信息掩密信道的容量。

从定义4-1和定义4-2可以看出，掩密信道容量的定义具有不同的观点，不管具体的信息嵌入、提取、鲁棒性，仅仅针对图像本身的特点来研究图像作为掩密信道的容量。针对具体的嵌入、提取算法并考虑其鲁棒性问题来研究容量。这两种研究都是有意义的，前者的研究有助于区别于传统信道容量，具有隐藏学科本身的特点，对该学科的发展具有理论意义，对在掩密通信中的应用也具有现实意义。后者的研究具有实际应用上的意义，也是值得重视的。因此，采取两种方式来研究图像掩密信道的容量，一种方法是，不管具体的信息隐匿和提取方法，只着眼一幅给定的图像中到底能隐藏多少比特的信息。另一种方法是，基于图像中嵌入水印的方法，利用传统信道的计算方法来研究其容量。于是，基于前者，给出图像信道容量定义如下：

定义4-3：能隐匿于掩护图像中的不被人类视觉系统感知的最大信息比特数。

类似地，对其他掩护信息（如话音、文本），可以得到更一般掩密信道容量的定义。

定义4-4：能隐匿于掩护信息中的不被人类感觉器官感知的最大信息比特数。

在这里“不被人类感觉器官感知”的含义是指，掩护信息和含密信息没有视觉上或听觉上的差别，其具体的衡量标准，可采用现有的图像、话音质量评价方法：主观评价和客观评价。在主观上，就采用视觉观察或听觉测试，虽然不够科学，但这是最直接和可靠的方法。

3.图像掩密信道的容量

（1）容量定义

定义4-3是很理想的定义，但不适合用计算图像作为掩密信道的容量，因为它仅考虑了图像的水平和垂直方向的纹理特征，并且实验表明，其容量嵌入法获得的含密图像的边缘处有明显的锯齿形出现。根据人的视觉系统HVS（Human Vision Srstem）的频率特性、方向特性、亮度特性和纹理特性。图像水印嵌入的BBP算法中，局部的加权函数ω^θ（i，j）就是对HVS特性的综合考虑，反映了图像的局部视觉掩蔽特性。因此，ω^θ（i，j）在一定程度上就体现了图像在该像素（i，j）位置能隐匿的信息量，将其应用到图像容量的定义中将是非常有利的，于是，给出如下的定义：

定义4-5：设图像A=[a（i，j）]_N×M，图像在像素位置（i，j）的局部方向掩蔽特性定义为

式中F（1，θ）、G（1，i，j）和C（1，i，j）按改进公式进行计算。其中θ=1，2，3分别表示水平、垂直和对角方向的容量的特性。定义

ω_A（i，j）=max[|ω_A¹（i，j）|，|ω_A²（i，j）|，|ω_A³（i，j）|] （4-20）称为在像素位置（i，j）的局部掩蔽特性。定义

称为图像A的总掩蔽特性。

定义4-6：（图像掩密信道容量掩蔽特性定义）设图像A=[a（i，j）]_N×M，ω_A（i，j）是图像在像素位置（i，j）的局部掩蔽特性，则图像在像素位置（i，j）的容量定义为

C_A（i，j）=log_βω_A（i，j） （4-22）

式中，β是可调控的参数，一般取2<β≤e=2.71828

图像的总容量C（A）定义为

因为是根据图像的掩蔽特性来定义的，因此，称为容量掩蔽特性含义，简记为“mc”定义。

图像每像素的平均容量定义为

根据上面的定义，得到如下关于图像掩密信道容量的定理。

定理4-1设图像A=[a（i，j）]_N×M，B=[b（i，j）]_N×M，如果ω（A）＜ω（B），则C（A）≤C（B）。

该定理的含义是：如果图像的总掩蔽特性小，其信息隐匿的容量也小。这符合直觉经验。定理的证明如下：(www.xing528.com)

证明：因为ω（A）＜ω（B），由式（4-21）有

上式（4-25）两边取对数得

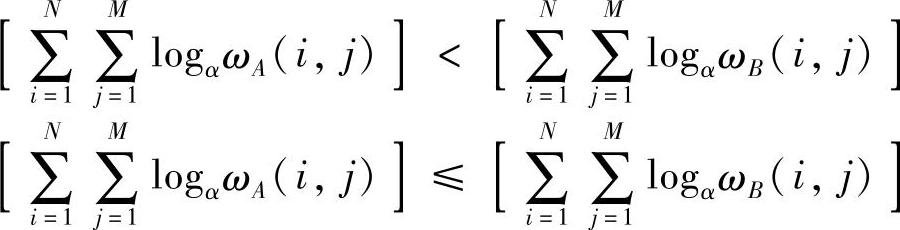
故由定义4-2有：C（A）≤C（B）

4.基于频率域水印的图像掩密

（1）水印信道模型

图像掩密信道的容量研究是在不考虑信息隐匿、提取算法以及隐匿信息鲁棒性的情况下，获得的图像掩密信道的容量，其信息隐匿容量可用“最低有效比特”（Least Significant Bit，LSB）算法来实现（隐匿信息的嵌入用算法5.1、隐匿信息的提取用算法5.2来实现），但要事先知道图像每个像素隐藏了多少比特信息，即隐藏提取算法是非盲时。但是，LSB隐匿方法其鲁棒性很差，为了增强鲁棒性，目前通常采用的是非加性水印嵌入方法。通过非加性水印容量计算的研究，在一幅图像中能隐藏多少个比特信息，可以在理论上给出一个上界，这在实际的掩密通信中对于掩护图像的选取是很有用的。

算法5.1嵌入过程——LSB信息隐匿算法

算法5.2提取过程——LSB信息隐匿算法

LSB算法的优点是隐匿的容量大，不可感知性好、计算复杂性低。

水印信道模型如图4-10所示。图中的水印嵌入和检测模型把水印问题看成扩谱数字通信问题，其中，水印被看成是要发送的消息，原始图像看成信道。在水印检测时，原始图像看成水印信息中的噪声。所以，能够用数字通信中的概念来分析基于数字图像水印的掩密通信问题。

如果把水印信道（Watermark Channel）模型化为加性高斯白噪声（AWGN）信道，则可用香农（Shannon）的信道编码理论。则有：

式中，C_w为水印信道容量；

P_wat为水印的能量；

P_host为掩护图像的能量。

用式（4-26）计算水印信道容量有以下两点不足：

①它仅适用于加性水印情况；

②仅适用于掩护图像可看成高斯噪声的情况。

目前所使用的水印技术具有抗攻击等较好的性质，同时也是目前较流行和较实用的水印嵌入技术。

图4-10 水印信道模型图

（2）扩展水印技术的容量问题

非加性的扩展谱水印嵌入方法为

式中，y_i为含水印图像的“离散余弦变换”DCT（Discrete Cosine Transformation）系数，可看成信道的输出；

x_i为被保护图像的DCT系数；

γ为水印的强度控制参数；

m_i为水印的第i个分量，可看成被传输的秘密信号。

因此，水印信道的数学模型可简化为如图4-11所示。

对于这样的水印信道，因为不能把DCT系数x_i模型化为高斯随机变量，加性白高斯噪声（AWGN）假定不成立，且噪声不服从高斯概率密度函数。因此，水印信道容量不能按式（4-26）来计算。

5.容量计算方法

（1）水印信道的数模型

假设f_mi（m）表示随机变量m_i的概率密度函数，f_xi（x_i）表示随机变量x_i的概率密度函数。因为m_i和x_i是独立分布的随机变量，所以下标可以忽略。根据式（4-27），在水印值m给定的条件下被加入水印的系数y的概率密度函数为：

图4-11 水印信道图

为了求每个DCT系数的容量，则要对输入m和输出y进行量化，于是变成了离散的输入和输出。又假设DCT系数相互独立，且m是独立均匀分布的随机变量，所以，水印信道是离散无记忆信道。

量化以后，则离散无记忆水印信道可完全由输入M=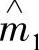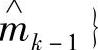，，…，、输出Y=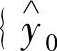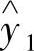，，…，和传输概率P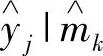（）所确定（j=0，1，…，J-1；k=0，1，…，k-1）。其中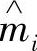，和分别表示输入输出量化值，传输概率可由式（4-28）积分得到，即

给定信道的传输矩阵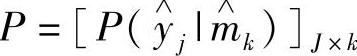和先验概率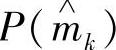，则信道的互信息为

于是，每个DCT系数的容量为

又因为I（M，Y）是P（M）=，，…P的凸函数，所以可将求水印信道和容量C_w的问题，表示成求解下列数学优化问题：

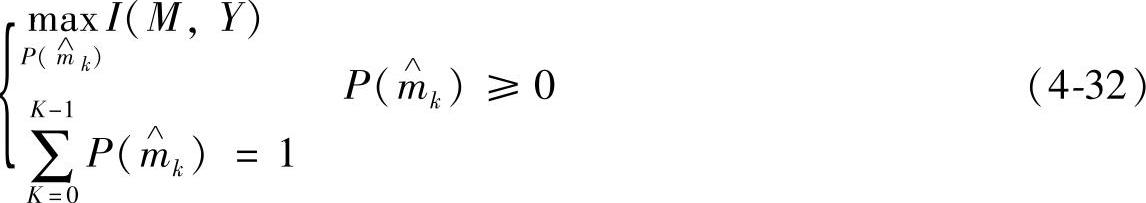
（2）DCT系数的数学模型

如果能求得信道的传输矩阵P，则可按信道容量迭代算法求出每个DCT系数的容量。下面讨论传输矩阵P的计算，要用到DCT系数的数学模型。

假定全帧DCT系数的分布服从如下的零均值广义高斯概率密度函数：

其中，，（·）是函数，参数v和α是正的实常数，控制概率密度函数的形状和方差。若v=1，则退化Laplace分布；v=2就是高斯分布。将式（8-28）中的f_x（y）用f_GG（x）代替，则有

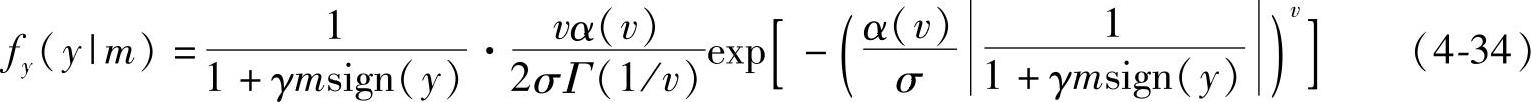
将式（4-34）代入式（4-29）有