扩频系统的干扰降噪优化

1.扩频技术的理论基础

香农（Shannon）公式指出，在高斯白噪声条件下，通信系统的极限传输速率（b/s）为

式中，B为信号带宽；

S为信号平均功率；

N为噪声功率。

若白噪声的功率谱密度为N₀，噪声功率N=N₀B，则信道容量C（b/s）可表示为

由式（3-25）看出B、N₀、S确定后，信道容量C就确定了。由香农第二定理可知，若信源的信息速率R小于或等于信道容量C，通过编码，信源的信息能以任意小的差错概率通过信道传输。使信源产生的信息尽可能高的信息速率通过信道，提高信道容量。

由香农公式可看出：

1）要增加系统的信息传输速率，则要求增加信道容量。增加信道容量的方法可通过增加传输信号带宽B，或增加信噪比S/N来实现，由式（3-24）可知，增加B比增加S/N更有效。

2）信道容量C为常数时，带宽B与信噪比S/N可互换，即可以通过增加带宽B来降低系统对此带宽中信噪比S/N的要求；也可通过增加信号功率，而降低信号的带宽。

3）当B增加到一定程度后，C增加缓慢了。由式（3-25）可知，随着B的增加，由于噪声功率N=N₀B，因而N也要增加，从而信噪比S/N要下降，影响到C的增加。考虑极限情况，令B→∞，C的极限值为

可见，在信号功率S和噪声功率谱密度N₀一定时，信道容量C是有限的。

2.扩频系统的物理模型

图3-16为扩频系统的物理模型。信源产生的信号经过第一次调制（信源编码）成为数字信号，再进行第二次调制（扩频调制），即用一扩频码将数字信号扩展到很宽的频带上，然后进行第三次调制，把经扩频调制的信号搬移到射频上发送出去。在接收端，收到发送的信号后，经混频后得到中频信号，再用本地扩频码进行相关解扩，恢复成窄带信号，然后进行解调，将数字信号还原。在接收过程中，要求本地产生的扩频码与发端用的扩频码完全同步。

图3-16 扩频系统物理模型图

a）发射 b）接收

3.直接序列扩频

图3-17为直扩系统的组成原理图，由信源输出的信号a（t）是码元持续时间为T_a的信息流，伪随机码产生的伪随机为C（t），每一伪随机码元宽度或切普（Chip）宽度为T_c，将信码a（t）与伪随机码C（t）进行模工加，产生一速率与伪随机码速率相同的扩频序列，然后再用扩频序列去调制载波，这样就得到已扩频调制的射频信号。

在接收端，收到的扩频信号经高放和混频后用与发端同步的伪随机序列对中频的扩频调制信号进行相关解扩，将信号的频带恢复为信息序列a（t）的频带，即为中频调制信号。然后再进行解调，恢复出所传输的信息a（t），从而完成信息的传输。对于干扰和噪声而言，由于与伪随机序列不相关，在相关解扩器的作用下，相当于进行一次扩频。干扰和噪声频谱被扩展后，其谱密度降低，大大降低了进入信号通道带内的干扰功率，使解调器的输入信噪比提高，从而提高系统的抗干扰能力。

图3-17 直扩系统组成图

a）发射 b）接收

直接系统信号分析，信号源产生的信号a（t）为信息流，码元速率R_a，码元宽度T_a（T_a=1/R_a），则

其中a_n为信息码，以概率P取+1和以概率（1-P）取-1，即

为门函数。

伪随机序列产生器产生的伪随机序列C（t），速率为R_C，切谱宽度为T_C（T_C=1/R_C），则

式中，C_n为随机码码元，取值+1或-1；

g_C（t）为门函数。定义与式（3-28）类似。

扩频过程实质是信息流a（t）与伪随机序列C（t）的模工加或相乘过程。伪随机码速率R_C比信息速率R_a大得多，一般R_C/R_a的比值为整数，且R_C/R_a＞＞1，所以扩展后的序列的速率仍为随机码速率R_C。扩展的序列

用此扩展后的序列去调制载波，将信号搬移到载频上去。用于直扩系统的调制，原则上大多数数字调制方式均可，应视具体情况，根据系统的性能要求来确定，用得较多的调制方式有BPSK、MSK、QPSK、TFM等。

采用PSK调制，用一般的平衡调制器就可完成PSK调制。调制后得到的信号

式中，ω₀为载波角频率。

接收端天线上感应的信号经高放的选择放大和混频后，得到以下部分的信号：有用的信号S_I（t）、信道噪声n_I（t）、干扰J_I（t）和其他网的扩频信号S_J（t）等，即收到的信号经混频后为

r_l（t）=S_I（t）+n_I（t）+J_I（t）+S_J（t） （3-32）

接收端的伪随机码产生器产生的伪随机序列与发射端产生的伪随机序列相同，但起始时间或初始相位可能不同，为C′（t）。解扩的过程与扩频过程相同，用本地的伪随机序列C′（t）与接收到的信号相乘后为

r_I′=r_I（t）C′（t）=S_I（t）C′（t）+n_I（t）C′（t）+J_I（t）C′（t）+S_J（t）C′（t）=S_I′（t）+n_I′（t）+J_I′（t）+S_J′（t）

分别对上面四个分量进行分析。信号分量S_I′（t），则

S_I′（t）=S_I（t）C′（t）=a（t）C（t）C′（t）cosω_It(www.xing528.com)

若本地产生的伪随机序列C′（t）与发射端产生的伪随机序列C（t）同步，有C（t）=C′（t），则C（t）·C′（t）=1。这样，信号分量为

后面所接滤波器的频带正好能让信号通过，可以进入解调器进行解调，将有用信号解调出来。

对噪声分量n_I（t）、干扰分量J_I（t）和不同网干扰S_J（t），经解调后，被大大削弱。n_I（t）分量为高斯白噪声，因而用C′（t）处理后，谱密度基本不变，但相对带宽改变，因而噪声功率降低。J_I（t）分量是人为干扰引起的，由于与伪随机码不相关，相乘过程相当于频谱扩展过程，将一干扰功率分散到一个很宽的频带上，谱密度降低，相乘后，接收滤波器的频带只能让有用信号通过，这样，能够进入到解调器输入端的干扰功率只能是与信号频带相同的那一部分。解扩前后的频带相差较大，因而解扩后干扰功率大大降低，提高了解调器输入端的信噪比，从而提高了系统的抗干扰能力。至于不同网的干扰S_J（t），由于不同网所用的扩频序列也不同。相当于再次扩展，从而降低了不同网信号的干扰。

图3-18和图3-19，分别表示直扩系统的波形图和频谱示意图。

下面分析直扩信号的功率谱。发送端的信号为

分析的方法是先求出S（t）的自相关函数B_s（τ），再进行傅里叶变换，得到S（t）的功率谱密度G_s（f），对S（t）求自相关函数，

由于a（t）与c（t）是由两个不同的信号源产生的，因而是相互独立的，则

B_d（τ）=B_a（τ）B_c（τ）

式中，B_a（τ）为a（t）的自相关函数；B_c（τ）为c（t）自相关函数。

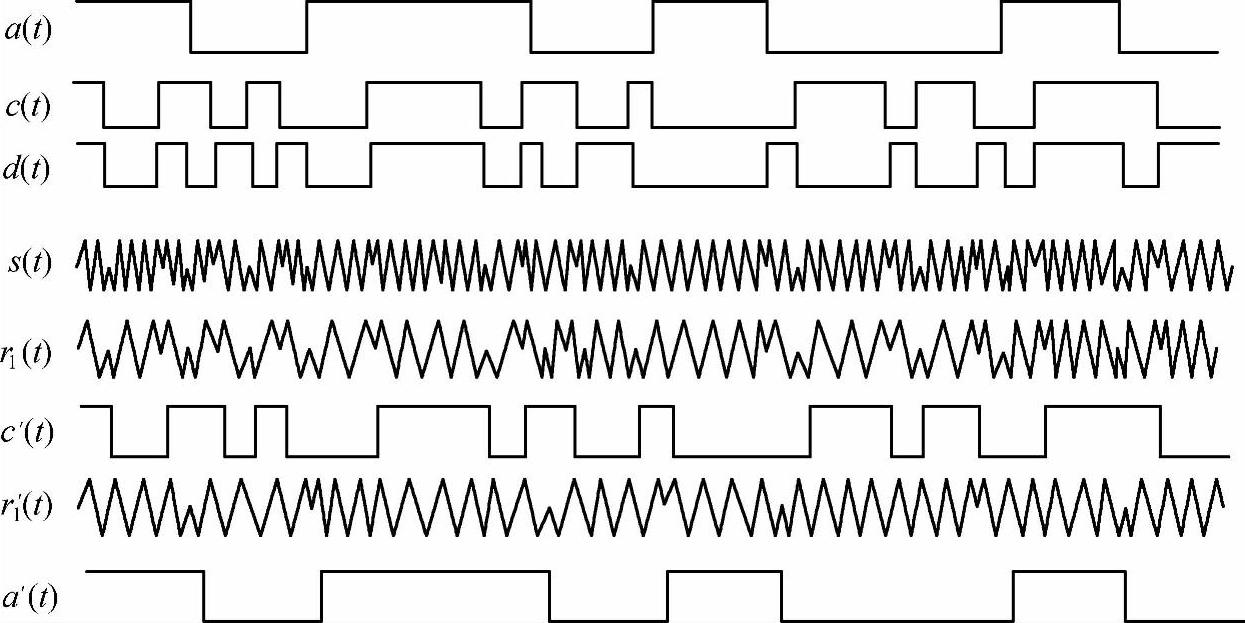
图3-18 直扩系统波形图

图3-19 直扩系统频谱示意图

c（t）是长度为N的周期性伪随机序列，故其自相关函数B_c（τ）也是周期为N的周期函数，其波形图如图3-20所示。

图3-20 B_c（τ）波形图

对B_c（τ）进行傅里叶变换得到c（t）的功率谱密度为

由式（3-36）可知，伪随机序列的功率谱是以ω₁=2π/NT₀为间隔的离散谱，其幅度由sinc²（ωT_c/2）确定，如图3-21a所示。

图3-21 直扩信号功率谱图

由傅里叶变换的性质可求出直扩信号S（t）的谱密度为

将式（3-36）代入，并考虑单返谱，则

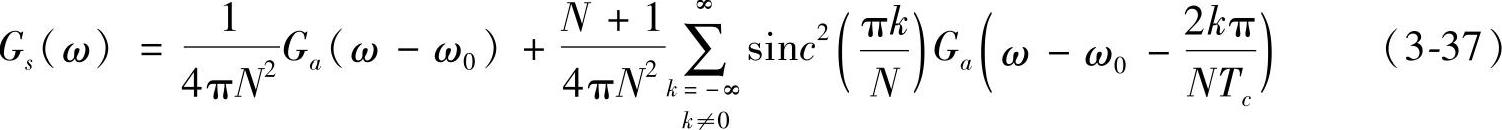
由图3-21b可知，N越大，G_c（N）谱线越密；T_c越小，功率谱的带宽越宽，谱密度越低，c（t）越接近白噪声。

4.处理增益

在扩频系统中，传输信号在扩频和解扩的处理过程中，扩展频谱系统的抗干扰性能得到提高。这种扩频处理得到的益处，称为扩频系统的处理增益。直扩系统的处理增益为

式中，R_ch为码片速率；

R为数据速率。

这里的码片是PN序列的一个脉冲，一般用分贝表示

对于直扩系统，解扩器的输出功率不变，但对于干扰而言，由于解扩过程相当于干扰的扩展过程，干扰功率被分散到很宽的频带上，进入解调器输入端的干扰功率相对解扩器输入端下降很大，即干扰功率在解扩前后发生变化。因此，对直扩系统，其处理增益就是干扰功率减小的倍数。

5.直扩系统的优点

在白噪声背景下，直扩系统的抗噪声性能实际上比窄带系统还要差一些，但有以下突出的优点：

1）具有强的抗干扰能力，能力的大小与处理增益成正比。利用扩频技术降低干扰功率是直扩系统的基本优势。

2）直扩系统信号的谱密度很低，具有很强的隐蔽性，可使信号淹没在噪声中，不易被敌方截获、侦察、测向和窃听。直扩系统可在-15～-10dB甚至更低的输入信噪比条件下工作，可借助系统接收机中的匹配滤波器的处理增益及编码增益，从背景噪声中恢复出微信号。

3）具有选址能力，可实现码分多址。

4）抗衰落，特别是抗频率选择性能好，直扩信号的频谱很宽，一小部分衰落对整个信号影响不大。

5）具有较强的抗多途径干扰能力，多途径信号到达接收端，由于利用了伪随机码的相关特性，只要多途时延超过伪随机码的一个切谱，则通过相关处理后，就可遏制多途干扰。

6）利用直扩系统伪随机码的相关特性，可实现高精度的测距和定位。