猫视觉皮层仿生的图像分割：实例分析

近年来，基于PCNN已被广泛应用于图像平滑、分割以及边缘检测等图像处理领域的研究中并显示了其优越性。

PCNN的数学方程描述为：

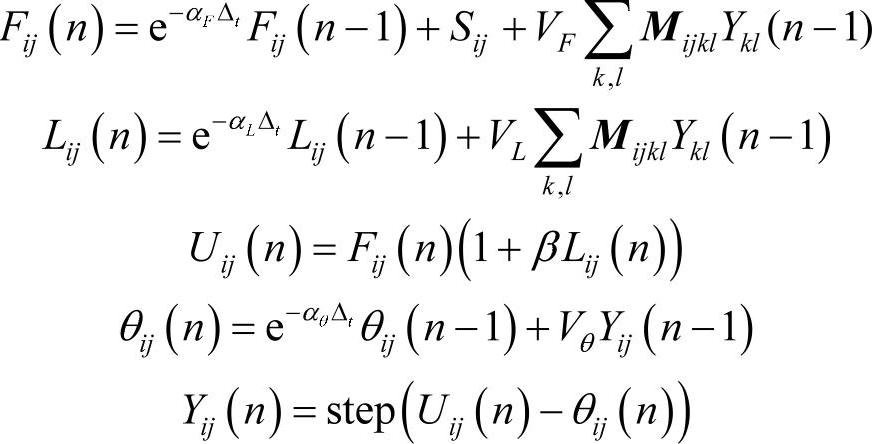
其中，ij为神经元的标号；S_ij、F_ij、L_ij、U_ij、θ_ij分别为神经元ij的外部刺激、馈送输入、链接输入、内部激活（即前突触势）、动态阈值；M和W为连接权矩阵；V_F、V_L、V_θ为幅度常数；β为链接系数；α_F、α_L、α_θ为相应的衰减系数；Δ_t为时间常数；n迭代次数；Y_ij为输出。

在用PCNN进行图像分割时，将一个二维PCNN网络M×N的个神经元分别与二维输入图像的M×N个像素相对应，像素ij的灰度值为网络神经元ij的外部刺激S_ij，且所有神经元的初始值设为1。则在第一次迭代时，神经元的内部激活U_ij（1）就等于外部刺激S_ij，若U_ij（1）≥θ_ij（1），这时该神经元输出为1，称其发生了自然点火，且其阈值θ_ij将急剧增大，然后随时间指数衰减。在此之后的各次迭代之中，点火的神经元会通过与相邻神经元的相互连接作用激励邻接的神经元，若邻接神经元的内部激活大于等于阈值则发生被捕获点火，显然，若邻接神经元与前一次迭代点火的神经元所对应的像素具有相似强度，则邻接神经元容易被捕获点火，反之不能够被捕获点火。因此，任何一个神经元的自然点火都会触发其邻接相似神经元的集体点火，这些点火的神经元形成一个神经元集群对应于图像中具有相似性质的一个小区域。因此，利用PCNN点火捕获的相似性集群特性便可进行图像分割。

例程7-1是运用PCNN算法进行图像分割的MATLAB源程序，运行结果如图7-21所示。

例程7-1

(www.xing528.com)

图7-21 例程7-1的运行结果

a）输入的原始图像 b）图像增强后的结果 c）图像分割后的结果