面向学习：探源比较总结

在数字图像处理中，很多算法是一脉相承或有着密切联系的，搞清楚这些来龙去脉以及相互联系，有利于加强对算法的理解以及改进创新。

那么，如何把握这些联系呢？首先要清楚每种算法的提出背景，即“这种算法为什么会被提出”或是“这种算法是针对什么问题而提出的”。以本书第2章中数字图像变换中的内容为例，这一问题是从图像的空间变换讲起的，但是空间变换无法反映图像的频率分布信息，随着傅里叶变换的诞生，这一问题得到了解决，傅里叶变换也被研究者誉为是“图像处理的第二种语言”。正在人们为之欢欣鼓舞之时，研究者有发现傅里叶变换也存在着不足，它在空域上无任何分辨，不能作局部分析。为此，D.Gabor于1946年提出了加窗傅里叶变换，也就是著名的Gabor变换，它通过引入一个时间局部化“窗函数”改进了傅里叶变换的不足，但其窗口大小和形状都是固定的，没有从根本上弥补傅里叶变换的缺陷。此时，小波变换的提出从根本上解决了这一难题，它有一个灵活可变的时间—频率窗，能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，“数学显微镜”的美誉也因此得来。如果读者能够把这些联系梳理清楚，那么，在学习小波变换时就会豁然开朗，应用也会游刃有余。难道小波变换就那么完美吗？答案当然是否定的，当前有很多算法就如何提高小波变换的效能提出了改进。按照上述的“联系”方式（见图7-3），就不难建立起完备的知识体系。

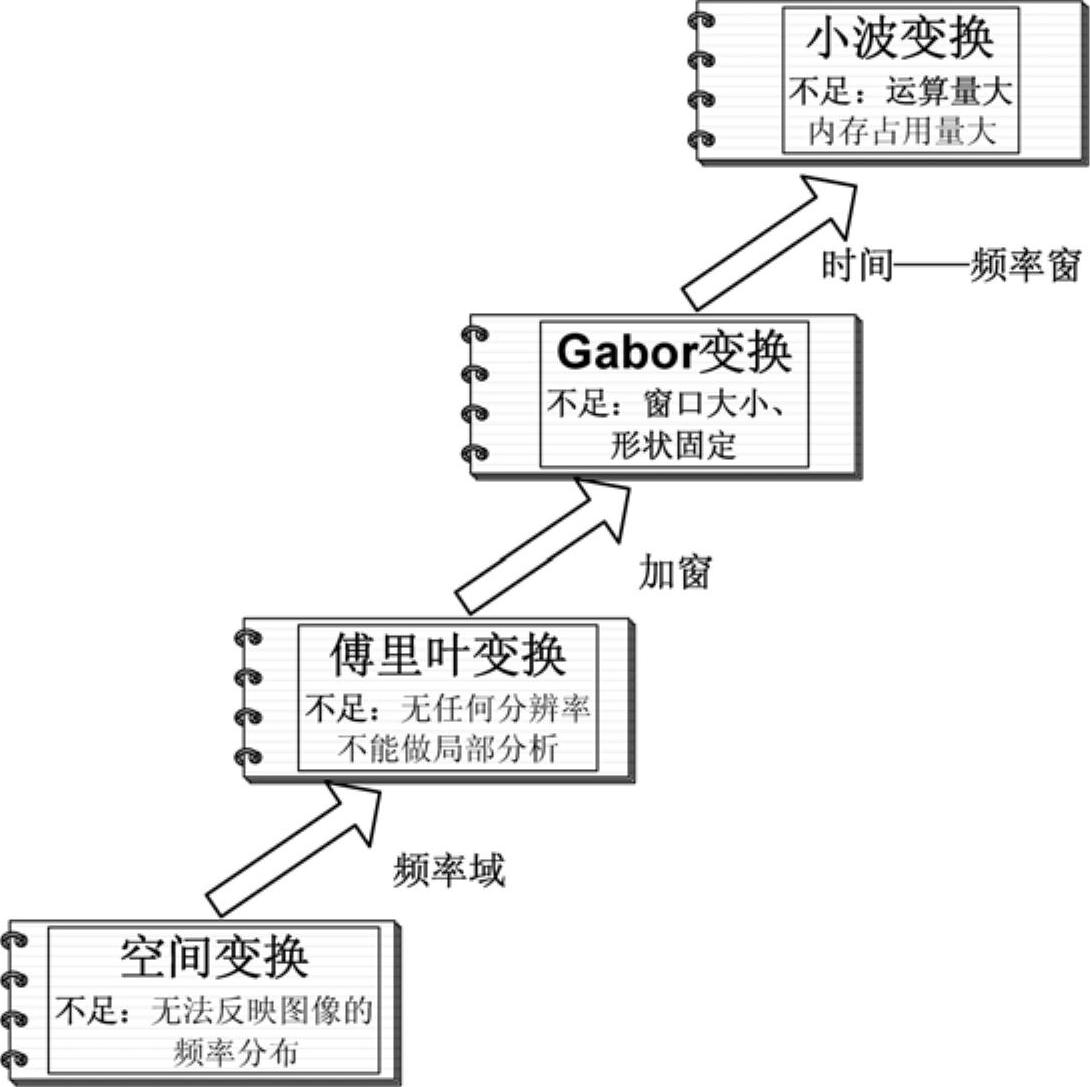
图7-3 图像分析联系示意图

谈过了“追根溯源”，再来聊聊“比较总结”，这里以本书4.3节图像的边缘检测为例来进行说明。在4.3节中，介绍了7种常用的边缘检测方法，每一种方法都能实现边缘检测，但对于同一幅图像，每一种边缘检测方法的效果又不尽相同。这是为什么呢？原来，每一种边缘检测的方法都有自己优点和不足，都有自己特定的应用背景，可以对其进行列表比较，如表7-1所示。

表7-1 边缘检测算子比较(www.xing528.com)

对各种边缘检测算子进行比较后，它们各自的特点便一目了然，在何种情况下运用哪种边缘检测算子效果最佳便做到了心中有数。

在比较完各种边缘检测算子的“个性”之后，再来总结一下它们的“共性”。尽管边缘检测的方法有很多，但各种方法的共同目的都是要检测出图像灰度变化剧烈的区域。从数学的角度来看，就是对数字图像进行差分；从信号处理角度看，就是用高通滤波器来保留高频信号。

学习的过程讲究循序渐进，温故知新，对数字图像处理技术的学习也不例外。但是，数字图像处理技术又有自身的特点，即理论深、角度广、更新快，因此，良好的学习方法可以使数字图像处理的学习事半功倍。在学习数字图像处理技术时，读者不妨尝试着去追根溯源、比较总结，相信定会受益匪浅。