基于SURF的图像拼接技术包括三大部分

基于SURF的图像拼接技术包括三大部分：特征点提取与匹配、图像配准、图像合成。

（1）特征点的提取与匹配

为了使拼接具有良好的精度和鲁棒性，同时又使其具有较好的实时性，本节采用2008年Bay等人提出的SURF算法完成图像序列特征点的提取。

SURF算法又称快速鲁棒特征，借鉴了SIFT中简化近似的思想，将DoH中的高斯二阶微分模板进行了近似简化，使得模板对图像的滤波只需要进行几个简单的加减法运算，并且这种运算与滤波模板的尺寸无关。实验证明，SURF算法较SIFT在运算速度上要快3倍左右，综合性能要优于SIFT算法。

SURF特征点提取与描述丰要包含4个步骤：

1)检测尺度空间极值。

2)精炼特征点位置。

3）计算特征点的描述信息。

4）生成描述特征点的特征向量。

SURF的匹配算法是通过计算两个特征点描述算子之间的欧氏距离得到的，即找出与特征点描述符pi欧氏距离最近和次近的两个邻居特征点来描述符qi′和qi″，然后计算pi与qi′以及pi与qi″两组描述符之间欧氏距离的比值r。如果比值r小于规定阈值则视为匹配成功，（pi，qi′）点对则为图像序列中的一对匹配点，否则匹配失败。这种匹配方法简便快捷，但会产生误匹配。针对上述问题，本节采用引导互匹配和投票过滤两种技术来提高匹配精度。

①引导互匹配法：该方法的思想是缩小特征点搜索范围，并采用互映射的方法减少错误匹配。假设图像变换矩阵的当前估计为H，根据对极几何特性，H规定了第一幅图像中的点x在第二幅图像中对极线Hx周围的搜索范围。因此，应在第二幅图像的对极线Hx周围的一定区域内搜索点x的匹配点。此外，根据互映射原理，即匹配点对之间的映射关系的对称性，对于匹配点对{pi⇔qi′}，在进行匹配映射时，应存在这两点间的对应关系{pi→qi′}和{pi←qi′}。因此，最终的匹配结果可表示为：（第一幅图像与第二幅图像进行引导匹配的结果）∩（第二幅图像与第一幅图像进行引导匹配的结果）。

②投票过滤法：使用投票过滤法消除误匹配的理论依据如下：在两幅相关的图像序列中，相机的旋转和尺度变化均相对稳定，因此连接图像中各组匹配点对所形成的向量之间的偏差应符合某一规律。如图6-1所示，假设图像1中的特征点pi和pi分别与图像2中的特征点qi′和qj′相对应，即{pi→qi′}与{pj→qj′}是正确的匹配点对，则向量Ei=qi′-pi与Ej=qj′-pi应具有相同特性（长度和方向）。本节综合考虑两方面因素，首先计算图像序列中所有匹配点对的横纵坐标距离差的平均值，并将其记为该图像序列组的标准匹配阀值。然后，删除图像序列组中横纵坐标距离差与标准匹配阀值相差太远的匹配点对。即采用删除横纵坐标之差距离平均值太远的错误匹配点对的投票过滤方法来提高匹配精度。

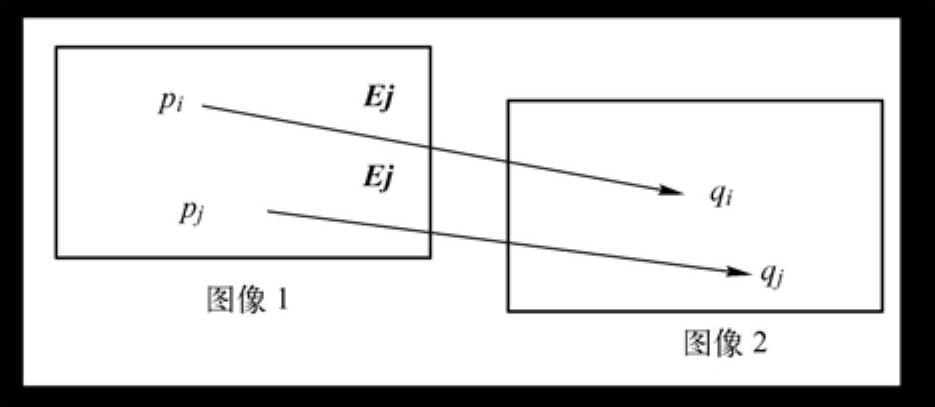
图6-1 消除误匹配

（2）图像配准

图像配准是一种确定待拼接图像间的重叠区域以及重叠位置的技术，它是整个图像拼接的核心。本节采用的是基于特征点的图像配准方法，即通过匹配点对构建图像序列之间的变换矩阵，从而完成全景图像的拼接。

变换矩阵H求解是图像配准的核心，其求解的算法流程如下。

1）检测每幅图像中特征点。

2）计算特征点之间的匹配。

3）计算图像间变换矩阵的初始值。(https://www.xing528.com)

4）迭代精炼H变换矩阵。

5）引导匹配。用估计的H去定义对极线附近的搜索区域，进一步确定特征点的对应。

6）重复迭代4）和5）直到对应点的数目稳定为止。

设图像序列之间的变换为投影变换

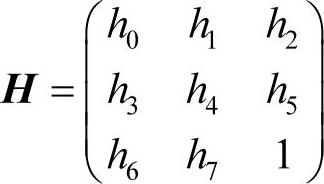
式中，H的自由度为8。设p=（x，y），q=q（x′，y′）是匹配的特征点对，则根据投影变换公式

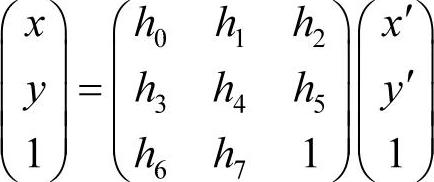
可用4组最佳匹配计算出H矩阵的8个自由度参数h_i=（i=0，1，⋯，7），并以此作为初始值。

为了提高图像配准的精度，本节采用RANSAC算法对图像变换矩阵进行求解与精炼，达到了较好的图像拼接效果。RANSAC算法的基本原理可通过图6-2来描述。

图6-2a中总共有7个点，其中有6个点属于内点（正确点），而第7个点属于外点（偏移点）。此时用最小二乘法拟合这组数据，得到的直线如图中虚线所示，显然这是错误的，此时实际的最佳拟合直线应该是那条穿越了前6个点的黑色实线。

RANSAC算法的思想简单而巧妙：首先随机地选择两个点，这两个点确定了一条直线，并且称在这条直线的一定范围内的点为这条直线的支撑。这样的随机选择重复数次，然后，具有最大支撑集的直线被确认为是样本点集的拟合。在拟合的误差距离范围内的点被认为是内点，它们构成一致集，反之则为外点。根据算法描述，可以很快判断，如果只有少量外点，那么随机选取的包含外点的初始点集确定的直线不会获得很大的支撑，如图6-2b所示。在图6-2a的例子中，经过RANSAC算法后，点7就会被剔除掉。然后再使用剩余的6个点进行最小二乘拟合，就会得到接近理想解的直线。值得注意的是，过大比例的外点将导致RANSAC算法失败。在直线拟合的例子中，由点集确定直线至少需要两个点；而对于透视变换，这样的最小集合需要有4个点。

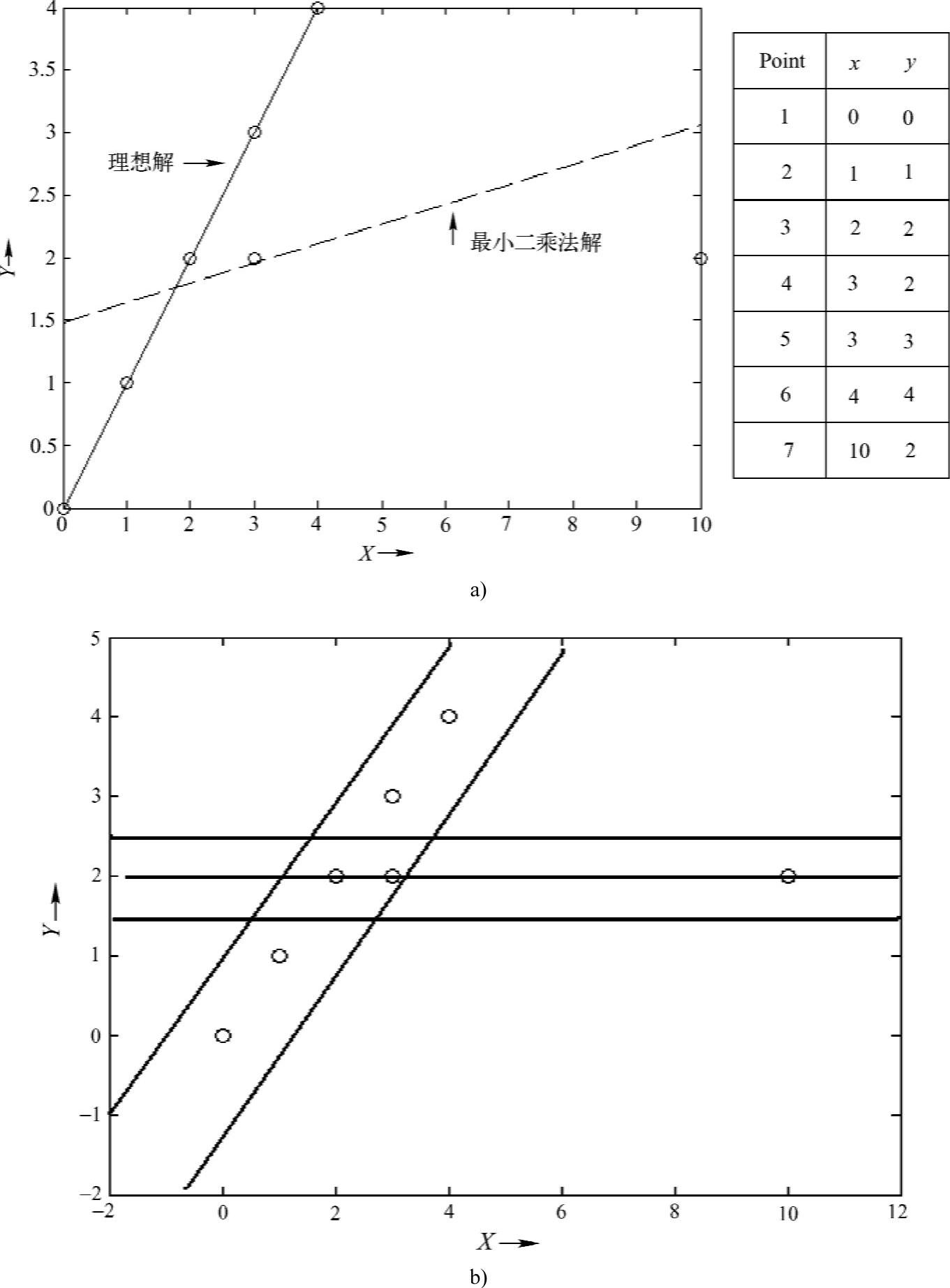
图6-2 RANSAC算法原理解释图

（3）图像合成

根据图像间变换矩阵H，可以对相应图像进行变换以确定图像间的重叠区域，并将待融和图像映射到到一幅新的空白图像中形成拼接图。需要注意的是，由于普通的相机在拍摄照片时会自动选取曝光参数，这会使输入图像间存在亮度差异，导致拼接后的图像缝合线两端出现明显的明暗变化。因此，在融和过程中需要对缝合线进行处理。进行图像拼接缝合线处理的方法有很多种，如颜色插值和多分辨率样条技术等，本节采用了快速简单的加权平滑算法处理拼接缝问题。该算法的主要思想是：图像重叠区域中像素点的灰度值Pixel由两幅图像中对应点的灰度值Pixel_L和Pixel_R加权平均得到，即Pixel=k×Pixel_L+（1-k）×Pixel_R，其中k是可调因子。图6-3为加权平滑算法图。

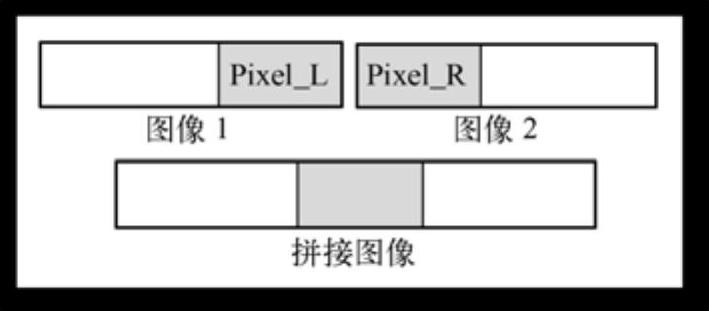
图6-3 加权平滑算法

通常情况下0＜k＜1，即在重叠区域中，沿图像1向图像2的方向，k由1渐变为0，从而实现重叠区域的平滑拼接。为使图像重叠区域中的点与两幅图像建立更大的相关性，令k=d1/（d1+d2），其中d1，d2分别表示重叠区域中的点到两幅图像重叠区域的左边界和右边界的距离。即使用公式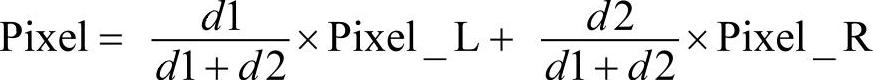进行缝合线处理。