识别算法的实现流程

使用神经网络识别不同目标时，首先需要用样本对神经网络进行训练，每一个样本由两部分组成：训练输入和期望输出。训练输入为一幅包含其中一个目标的图像，而期望输出为该目标所对应的期望值。

为了获得准确的识别结果，需要用大量样本对网络进行训练，即需要大量的图像序列。但是，一幅图像中包含着大量的信息，不但对于识别没有帮助，还使得网络训练十分困难。为此，本书采用求取不变矩的方法将一幅图像转化为包含7个数字的一组不变矩。具体的方法是求取每一幅图像的不变矩，将这个图像对应的不变矩和图像中目标的代号作为一组训练样本。这样获得的训练样本将大大简化，减少了干扰因素，缩短了训练时间，提高了识别准确率。

但是在求不变矩之前，还需要对图像进行一定的预处理，尽可能滤除干扰，并将图像二值化，为求不变矩做好准备。

在得到相应的训练样本之后，建立BP神经网络，并使用这些训练样本训练网络。训练结束之后就可以使用神经网络来识别并分类工具了。最后，为了进一步提高识别的准确率，利用强分类器提升网络性能。

由此，识别算法的实现流程可以依次分为下面的一些步骤。

1）获取图像序列。获得所要识别对象各个角度的图像。

2）图像预处理。二值化为适合求不变矩的图像。

3）求不变矩。求预处理之后图像的不变矩，所得到的不变矩具有平移、旋转、尺度不变性。

4）生成神经网络的训练样本。将得到的不变矩和对应的期望输出作为神经网络的训练样本，并且由于样本集包含了所要识别目标各个角度的图像，又经过求不变矩具有了平移、旋转和尺度不变性，所以保证了样本集的完备性。

5）建立神经网络。建立一个BP神经网络。

6）训练神经网络。设定训练条件，并使用得到的样本对网络进行训练。

7）识别目标。使用训练好的网络识别目标，此处的目标指的是一组不变矩。

8）网络性能优化。使用强分类器进一步提升网络表现。

下面就来看一看每一步具体是如何执行的。

（1）获取图像序列

为了获得一个完备的训练样本，我们按照几个工具的真实大小和比例关系，使用Pro/E软件在计算机中建立了对应的仿真模型。并将其导入三维渲染软件3dsmax软件中进行渲染，以期望尽可能得到接近的仿真情况。对于如何按照目标物体建立与其相对应的模型，以及如何进行渲染，这个问题有较为成熟的解决方法，且不是本章重点，故在此不作过多讨论。需要注意的是，为了方便后续图像采集，尽量将造型时的坐标原点建立在物体中心位置。那么，剩下来的问题即为如何获取图像样本集。

如上文所述，目标图像的采集目的是要得到目标物体各个角度的图像。由于物体在造型软件中可以围绕原点进行定点转动，摄像机和物体相对位置固定时，可不考虑空间平移的情况，于是问题的关键就是：通过什么样的旋转方式可以获得目标各个方向的图像。首先通过造型软件建立所要识别目标物体的仿真模型，并建立其空间运动的数学模型如图5-11a所示。

通过造型软件建立所要识别目标物体的仿真模型，并建立其空间运动的数学模型。在图5-11a中，Oxyz为物体所在空间坐标系，Ox′y′z′为固联在物体上的随体坐标系。物体围绕原点O转动，其在空间的任意姿态可以通过进动角ψ、章动角θ、自旋角ϕ来决定，如图5-11c所示。由图5-11c可以看出，当物体只发生进动时，其围绕z′轴转动，进动后物体上任意点在空间坐标系的坐标（x，y，z）与在随体坐标系的坐标（x₁，y₁，z₁）存在如下变换关系。

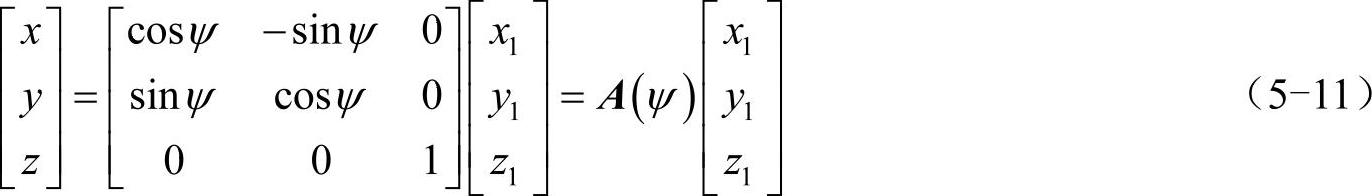
其中，进动变换矩阵

同理，可得物体的章动变换矩阵A（θ），自旋变换矩阵A（ϕ）。其中

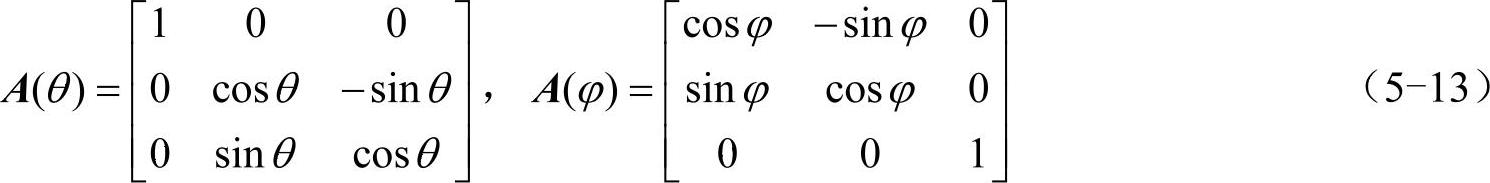
物体上任意点在空间坐标系的坐标（x，y，z）与在随体坐标系的坐标（x′，y′，z′）存在如下变换关系。

显然，通过依次改变ψ、θ、ϕ三个参数就可以获得物体在空间各个角度的图像（见图5-11c）。但是这种方法需要进行大量的计算，实际操作也很困难。通过分析可以发现，后面所要使用的不变矩方法具有旋转变换不变性，这也就意味着物体围绕垂直于成像平面的轴旋转对识别不产生影响。利用这一特性，我们可以将采集图像时的旋转模型简化。

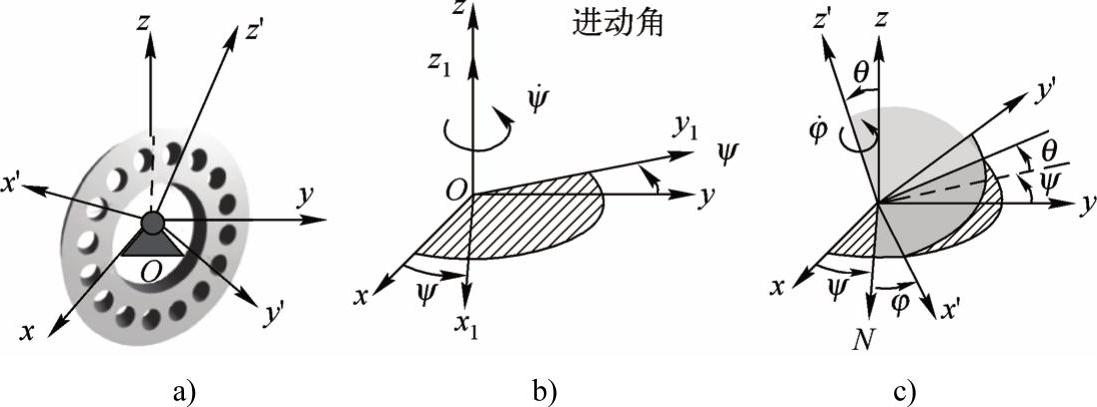
图5-11 物体在空间坐标系中的表示

a）空间坐标系和随体坐标系 b）进动运动 c）空间任意点的变换

如图5-12所示，摄像机在采集物体图像时，M为图像中心，M′为物体旋转中心，成像平面α与过M′的β平面垂直，MM′为过图像中心且垂直于α平面的直线，物体在绕MM′轴的旋转运动不影响识别。于是，不妨将MM′直线取作进动运动的Z′轴，则物体在Z′轴周向不发生进动运动，即在图像中旋转只发生在自转轴b_i随章动运动θ运动到垂直于成像平面时。此时，物体上任意点在空间坐标系的坐标（x，y，z）与在随体坐标系的坐标（x′，y′，z′）变换关系可简化为式（5-15）：

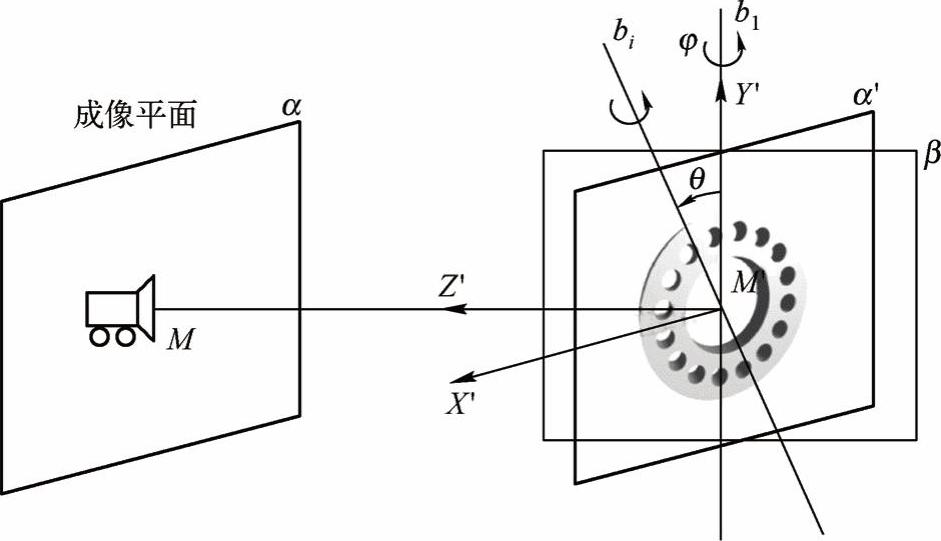
图5-12 目标旋转和图像采集

取物体上任意一点P，其在随体坐标系下的坐标为（x′_P，y′_P，z′_P），M′为物体的随体坐标系原点和旋转中心，P到M′的距离R_P始终不变，为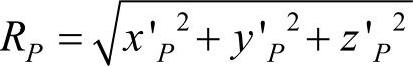。经过推导可以得到P点的另外一个坐标表达式：

式（5-16）即为P点在随体坐标系下的球面坐标表达式，这意味着通过改变θ和ϕ的值，P点可以出现在以M′为圆心R_P为半径的球面上。上述公式证明了通过改变章动角θ和自旋角ϕ就可以得到物体各个方向的图像。

本文所采取的图像采集策略为通过依次改变章动角θ和自旋角ϕ的值来获得模型目标的图像。采用的镜头焦距为43.46mm，视场角为45°。图5-13所示为三种工具的章动角从100°到190°过程中采集到的若干图像。本文侧重于对方法的讨论，所以采用每次旋转10°的方法，即章动角每转过10°，自转一周。这样，当章动角转过一周后，每个工具模型可以得到1296幅图像。依照这个方法得到的图像就构成了神经网络训练的样本集合。

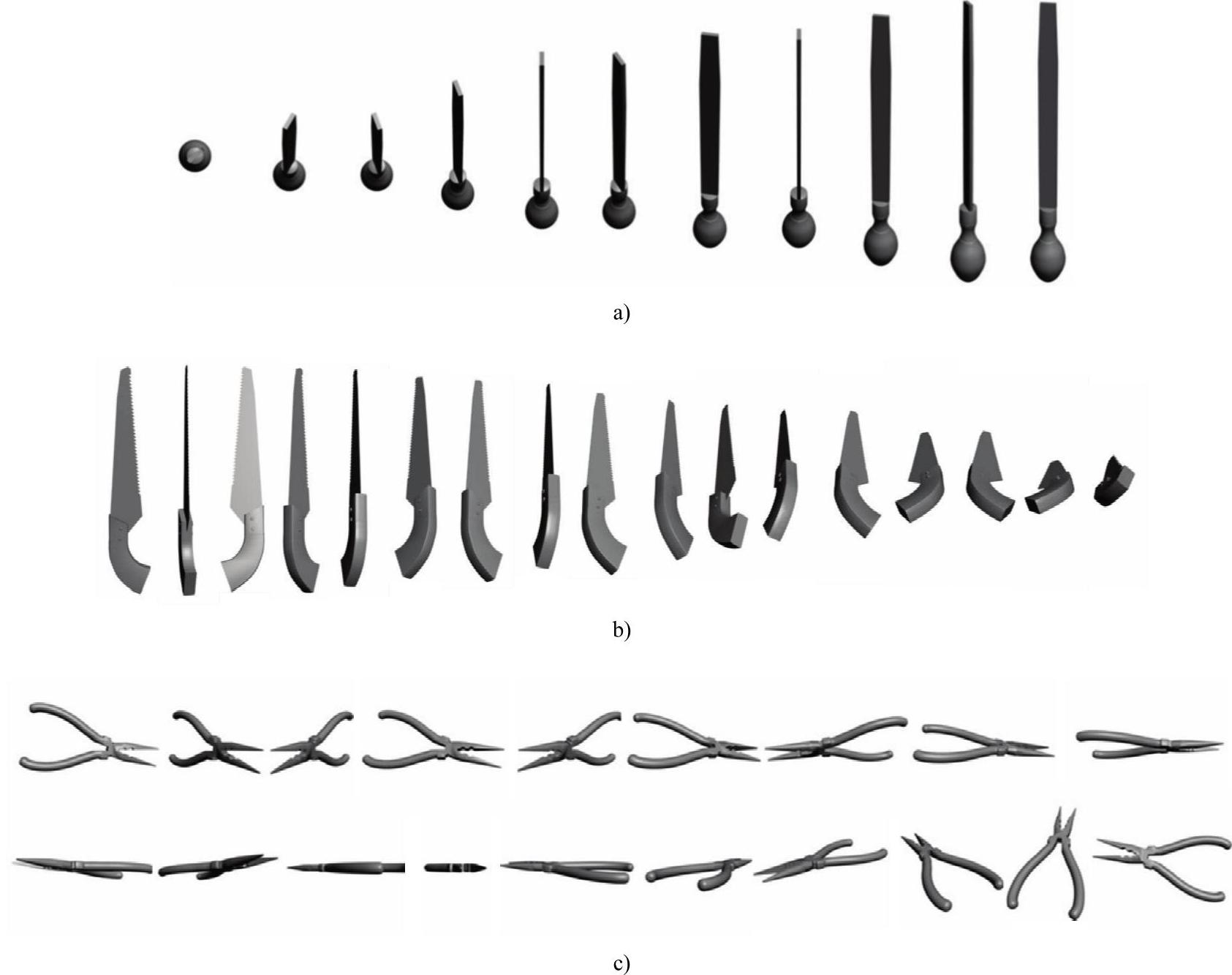
图5-13 三种工具模型在章动角100°～190°时取出的若干幅图像示意

a）锉子模型 b）锯子模型 c）钳子模型

由于这些工具为左右对称结构，实验采集从0°至190°的711幅图像，三个工具总共采集2133幅图像。

该方法的主要优势在于可以较为方便地获得三维目标各个角度的图像，节约了成本。但需要说明的是，该方法对于仿真程度和预处理结果依赖较大，对于背景、光照和物体表面材质较为敏感。减小采样间隔（采集时每次旋转的角度），以及提高仿真程度（模型和场景的真实程度），能够有效提高使用该方法时的识别正确率。

（2）图像预处理

由于需要对目标求不变矩，而且目标属于形状特征明显而纹理特征不明显的类型，尝试将其转化为二值图像以方便求不变矩。较为合适的预处理方法有二值化。之所以不适用滤波和去噪是因为此处所使用的图像为计算机生成，不存在噪声，并且求不变矩后噪声的影响几乎可以忽略不计。经过二值化后的图像如图5-14所示。

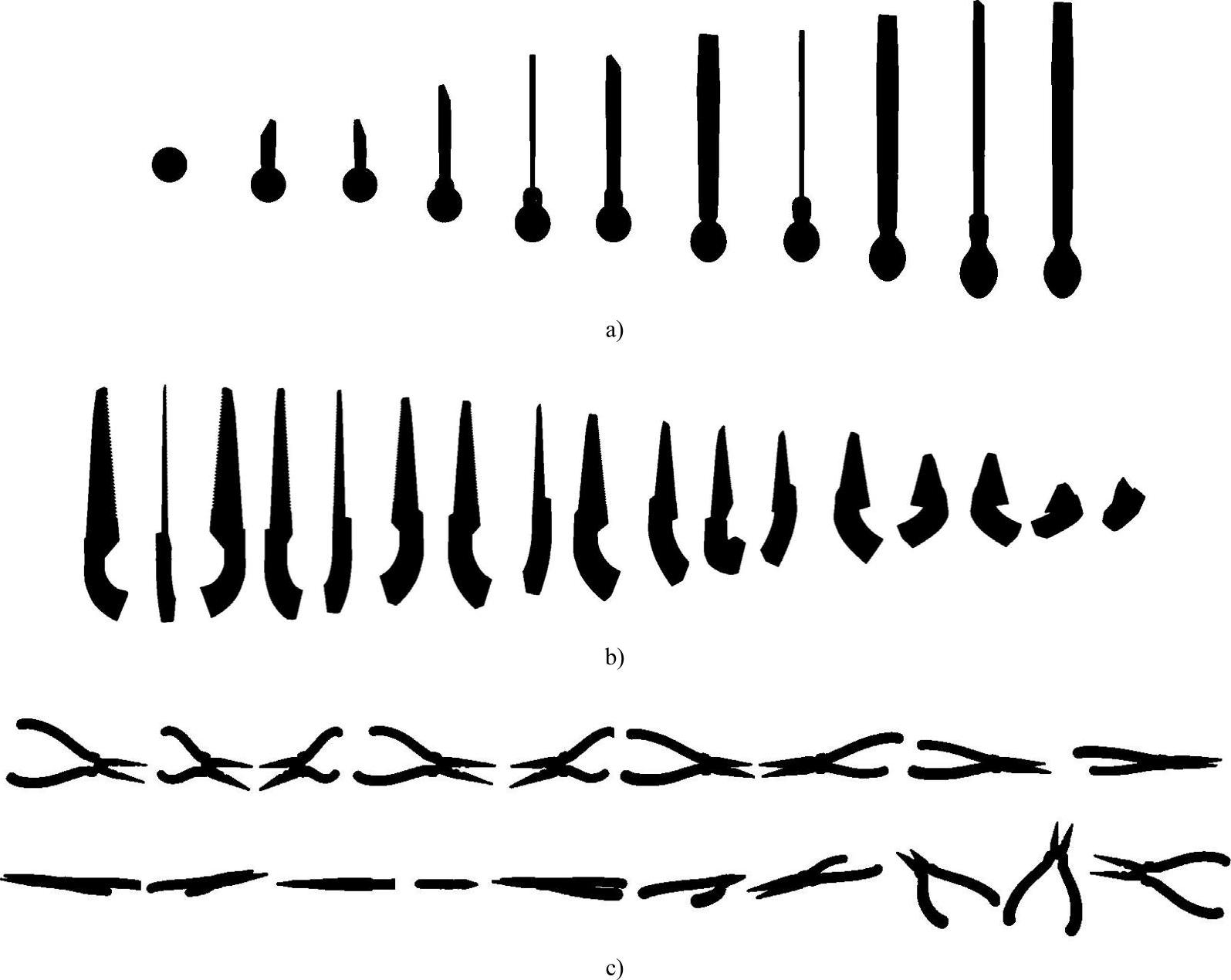
图5-14 二值化处理三种工具模型

a）锉子模型 b）锯子模型 c）钳子模型(www.xing528.com)

（3）求图像的不变矩

在得到物体各个角度的图像之后，还需要消除目标在图像中的位置、大小和旋转的影响。使用不变矩可以达到消除上述影响的目的。不变矩的提取方法详见本书的第四章的4.1节。

（4）生成神经网络的训练样本和识别样本

对预处理后的每一幅图像，求其对应的7个不变矩，得到一个向量序列，该向量序列加上目标输出即成为神经网络训练样本。而识别样本只包含7个不变矩。本实验中，期望输出用001代表锯子，010代表锉子，011代表钳子。

（5）建立神经网络

本文采用BP神经网络进行目标识别实验。网络结构如图5-15所示，设计成单隐含层结构，隐层包含20个神经元，隐层神经元传递函数为S型函数；输出层含有3个神经元，其传递函数为线性函数。

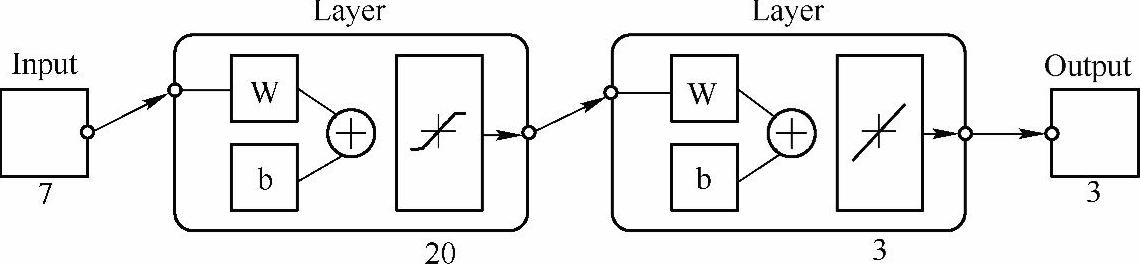
图5-15 识别用BP神经网络结构

（6）训练神经网络

所使用的网络训练方法为Levenberg-Marquardt算法，其权值调整可按式（5-17）进行：

其中J为误差对权值微分的Jacobian矩阵，E为误差向量，m为一个标量。

以上方法利用了近似的二阶导数信息，既具有高斯-牛顿法的局部收敛性，又具有梯度下降法的全局特性，但比梯度算法收敛速度快很多，并且算法稳定。

本文中，设置训练误差限0.00004，训练步长0.1，训练周期300。训练情况如图5-16所示。

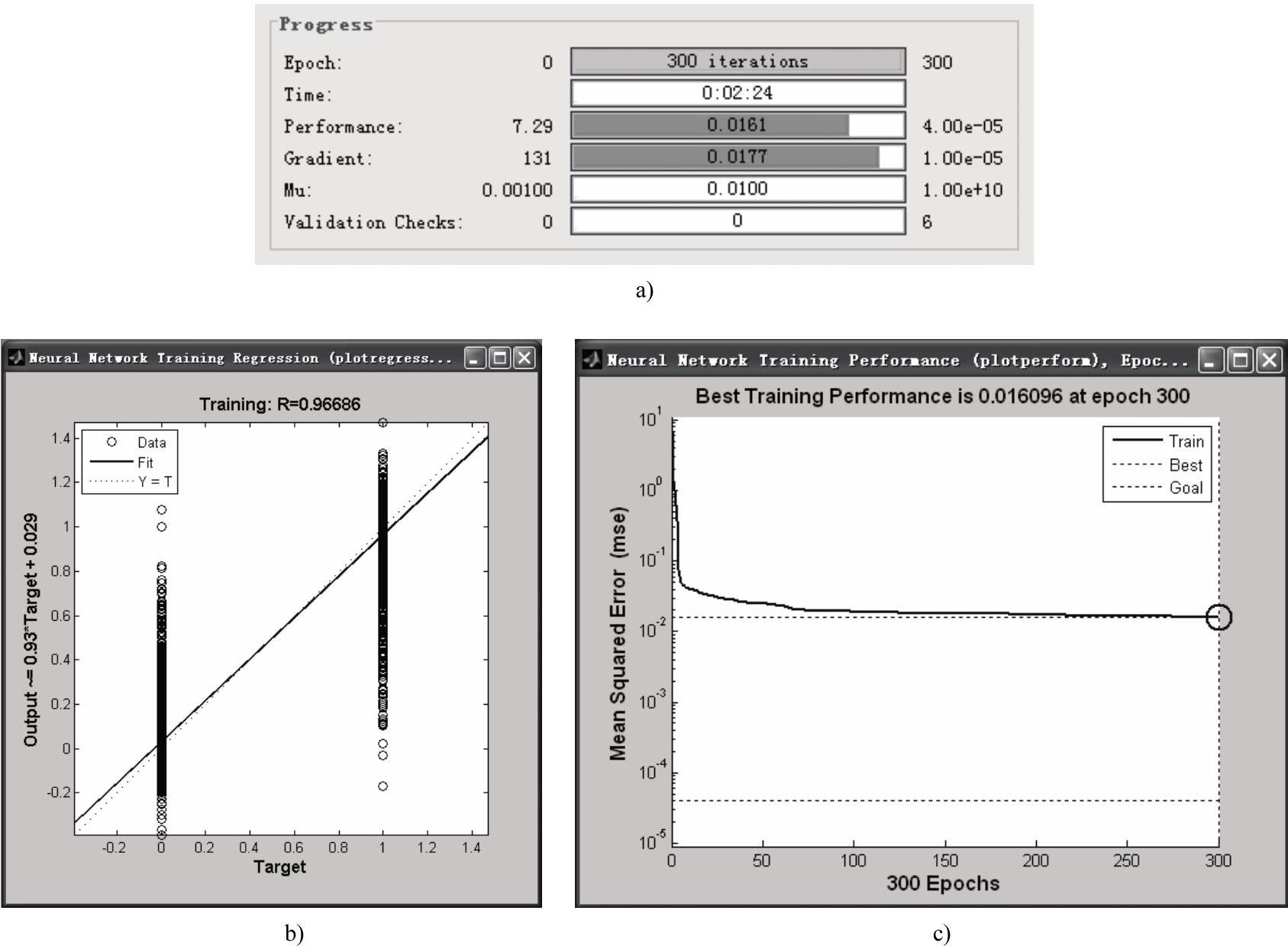
图5-16 网络训练情况

a）网络训练参数 b）训练输出 c）网络表现随训练周期的曲线

（7）识别目标

整个网络的训练和识别过程如图5-17所示，训练过程需要图像的7个不变矩和期望输出；而识别过程中，将待识别图像的7个不变矩输入神经网络，网络将给出识别判断的结果。

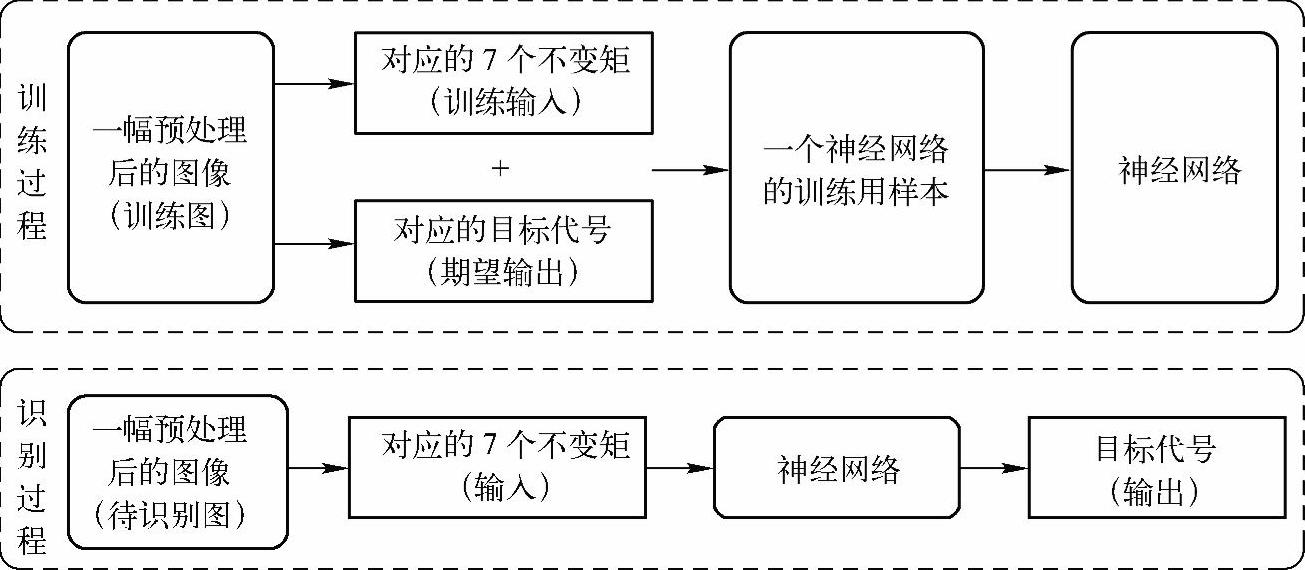
图5-17 神经网络训练和识别流程

为保证能够同步采样，在仿真软件中架设另外一架与采样摄像机参数相同但位置不同的摄像机以采集测试样本。对上述三个工具模型随机采集33幅图，总共99幅图作为测试样本。实际识别的对象是经过计算得到的99组不变矩。将这99组不变矩输入训练好的网络，得到的输出即为识别结果。

（8）网络性能优化（自适应强分类器，理论简单介绍）

为了进一步提升网络的识别正确率，采用自适应强分类器（ada-boost）算法构建一个神经网络的强分类器。该方法通过训练时分类的正确与否调整用于下一个网络训练的数据的权重，从而使得网络性能得到提升，并根据多个神经网络的综合表现决定输出，得到的正确率高于单个神经网络。

Ada-boost理论由Freund和Schapire在1995年提出，这是一种将弱学习算法融合为强学习算法的方法，其基本思想是：首先判断每次训练后每个样本的分类是否正确，结合上一次的分类情况，改变对应的训练样本在学习过程中的权重。对于分类正确的样本，降低其在下一次训练中的权重；而对于分类错误的样本，增加其在下一次训练中的权重。这样，分类错的那些样本就因被赋予了较高的权重而凸显了出来，从而得到一个新的样本分布。最后，将每一次训练得到的分类器融合起来，作为最终的分类器。其中，每一次训练得到的分类器称为弱分类器，最终得到的决策分类器称为强分类器。

其主要步骤为：首先，给出样本空间和弱学习算法，从样本空间得到m组训练数据，并将每组训练数据的权重都设为1/m；然后开始训练弱分类器，每次训练之后，根据分类的正确与否更新训练数据权重，正确分类数据赋予较小权值，错误分类数据赋予较大权值。经过多次训练，得到多个分类的函数序列，每个弱分类器为一个分类函数。也将权重引入这些分类函数，即分类结果越好的函数，对应的权重越大。最终的强分类函数由弱分类函数加权得到。对应的处理流程如图5-18所示。

该方法的优点是，不管使用哪类神经网络，都可以用该方法来对其识别正确率进行提升，是一种适用范围广泛的网络性能提升方法。

图5-18 强分类器处理流程

如图5-19所示，ada-boost方法的具体实施步骤包括数据选择和网络初始化、弱分类器预测、计算分类权重序列、训练数据权重调整和构建强分类函数等。

图5-19 ada-boost强分类器实现过程

1）数据和网络初始化。从样本空间中随机选择m组训练数据，将每组数据的分布权值初始化为D_t（i）=1/m，根据样本输入输出维数确定神经网络输入层和输出层结构，初始化神经网络权值和阈值。

2）弱分类器预测。训练第t个弱分类器时，用训练数据训练神经网络并预测训练数据输出，且可按公式（5-18）计算分类序列g（t）的分类误差和e_t，

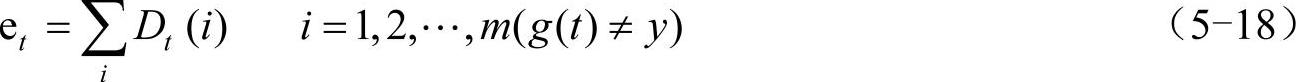
式中，g（t）为预测分类结果；y为期望分类结果。

3）计算分类权重序列。根据分类序列g（t）的分类误差e_t计算序列的权重a_t，权重计算公式如式（5-19）所示：

4）训练数据权重调整。根据分类序列权重a_t调整下一轮训练样本的权重，调整公式如下。

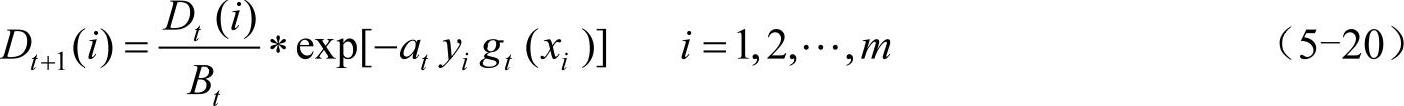
式中，B_t是归一化因子，目的是在权重比例不变的情况下使分布权值和为1。

5）强分类函数。假设训练T轮后得到T组弱分类函数f（g_t，a_t），由T组弱分类函数f（g_t，a_t）和调整权重α_t组合得到了强分类函数h（x），且有：

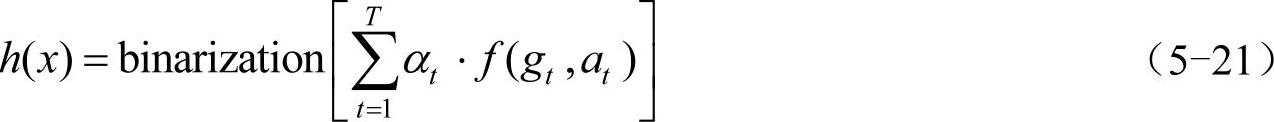
由于本文中训练输出为0和1的二值数据，所以对结果进行二值化处理。处理的流程如图5-20所示。

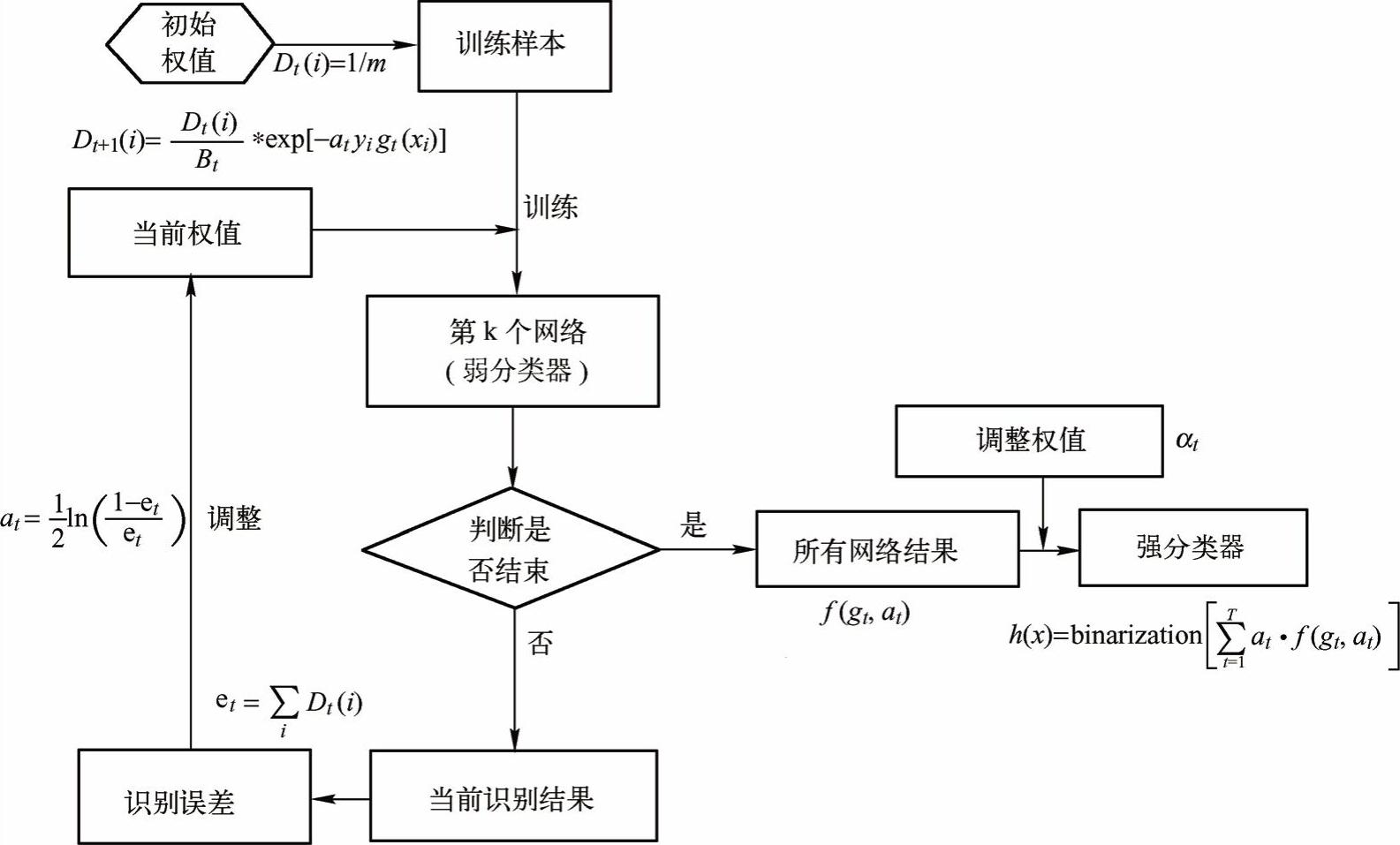
图5-20 自适应强分类器实现流程