尺度空间表示优化方法

通常要想获取不同尺度的斑点，必须建立图像的尺度空间金字塔。一般的方法是通过采用不同σ的高斯函数，对图像进行平滑滤波，然后，重采样图像以获得更高一层的金字塔图像。Lowe在SIFT方法中就是通过相邻两层图像金字塔相减得到DOG图像，然后再在DOG图像上进行斑点和边缘检测工作的。

由于采用了盒子滤波和积分图像，所以并不需要像SIFT算法那样去直接建立图像金字塔，而是采用不断增大盒子滤波模板尺寸的间接方法。通过不同尺寸盒子滤波模板与积分图像求取Hessian矩阵行列式的响应图像，然后，在响应图像上采用3D非最大值抑制，求取各种不同尺度的斑点。

如前所述，使用9×9的模板对图像进行滤波，其结果作为最初始的尺度空间层（此时，尺度值s=1.2，近似σ=1.2的高斯微分），后续的层将通过逐步放大滤波模板尺寸，以及放大后的模板不断与图像进行滤波得到。由于采用盒子滤波和积分图像，滤波过程并不随着滤波模板尺寸的增加而使运算工作量增加。

与SIFT算法类似，我们需要将尺度空间划分成若干组（Octaves）。一个组代表了逐步放大的滤波模板对同一输入图像进行滤波的一系列响应图。每个组又由若干固定的层组成。由于积分图像离散化的原因，两个层之间的最小尺度变化量是由高斯二阶微分滤波器在微分方向上对正负斑点响应长度l₀决定的，它是盒子滤波模板尺寸的1/3。对于9×9的盒子滤波模板，l₀为3。下一个层的响应长度至少应该在l₀的基础上增加2个像元，以保证一边一个像元，即l₀=5，这样，模板的尺寸就为15×15，如图4-27所示。以此类推，可以得到一个尺寸逐渐增大模板序列，它们尺寸分别为：9×9、15×15、21×21、27×27、39×39，黑色、白色区域的长度增加偶数个像元，以保证一个中心像元的存在。

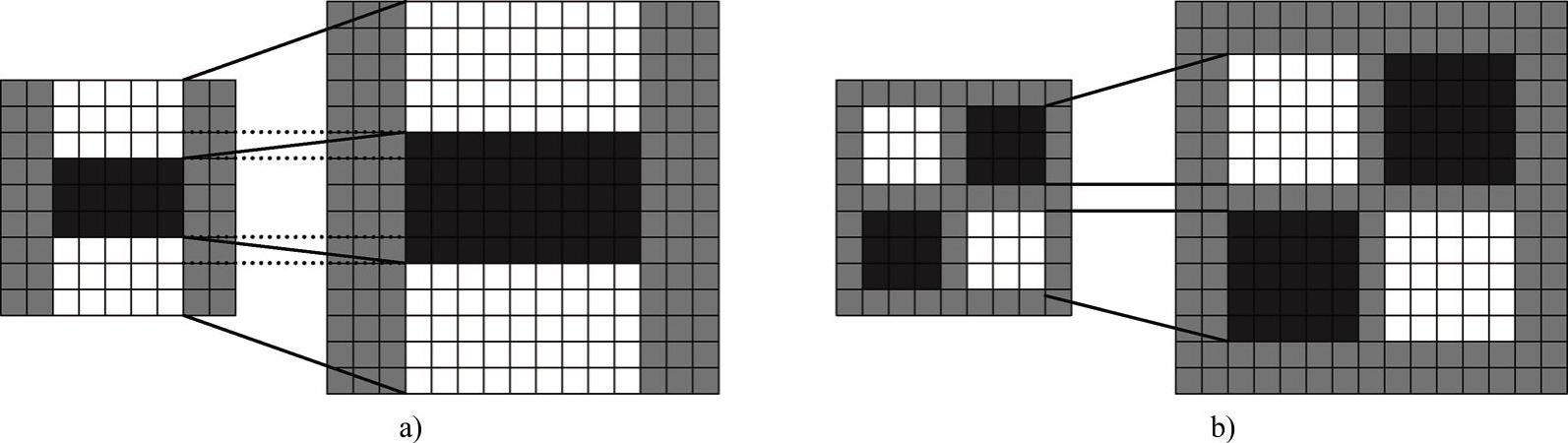
图4-27 滤波模板D_yy和D_xy尺寸从9×9增大到15×15时的变化

采用类似的方法来处理其他组的模板序列。其方法是将滤波器尺寸增加量翻倍（6、12、24、48）。这样，可以得到第二组的滤波器尺寸，它们分别为15、27、39、51；第三组的滤波器尺寸为27、51、75、99。如果原始图像尺寸仍然大于对应的滤波器尺寸，尺度空间的分析还可进行第四组，其对应的模板尺寸分别是51、99、147和195。图4-28给出了第一到第三个组的滤波器尺寸变化的图形表示。对数水平轴代表尺度，组之间有相互重叠，其目的是为了覆盖所有可能的尺度。在通常尺度分析情况下，随着尺度的增大，被检测到的斑点数量迅速衰减。与此同时，为了减少运算量，提高计算的速度，可以考虑在滤波时，将采样间隔设为2°。

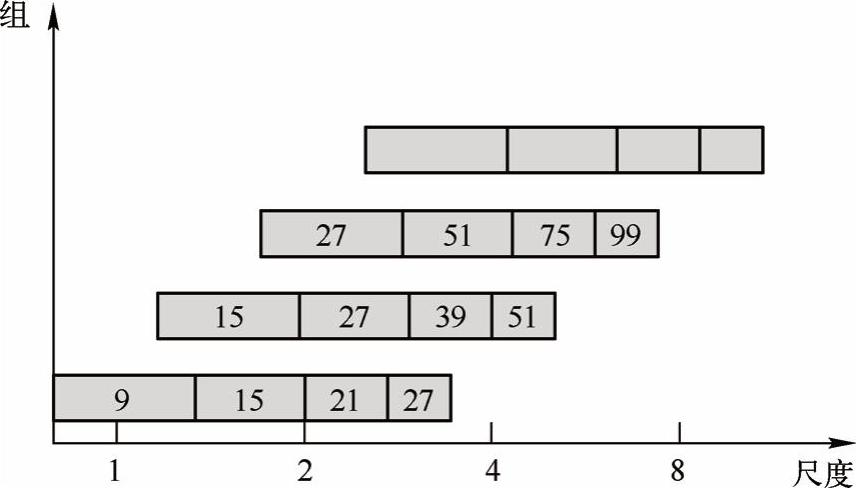
图4-28 三个不同组的滤波器尺寸的图形化表示

仿照SIFT算法，滤波响应长度l、滤波器的尺寸L、组索引o、层索引s、尺度σ之间的相互关系为(www.xing528.com)

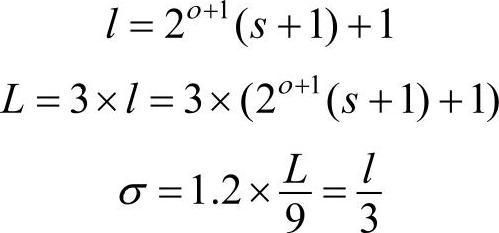
滤波器可以采用矢量数据结构来表示。数据结构中分别包含滤波器中每个盒子的坐标、盒子中的填充值和盒子的面积等信息。坐标既可以滤波器中心像元为原点，也可以左上角像元为原点。

图4-29所示为不同尺寸时的滤波器模板的图形化表示。

图4-29 不同尺寸时的滤波器模板的图形化表示

a）尺寸为15

图4-29 不同尺寸时的滤波器模板的图形化表示（续）

b）尺寸为21 c）尺寸为27