SIFT算法：图像特征提取的强大工具

Lowe总结了现有的特征提取方法，并提出了一种新型高效的特征检测描述方法——SIFT（Scale Invariant Feature Transform）。SIFT的主要思路是：首先建立图像的尺度空间表示，然后在尺度空间中搜索图像的极值点，由极值点再建立特征描述向量，最后用特征描述向量进行相似度匹配。采用SIFT方法提取的图像特征具有放缩不变性、旋转不变性，仿射不变性，还有一定的抗光照变化和抗视点变换性能。该特征还具有高度的可区分性，能够在一个具有大量特征数据的数据库中进行精确地匹配。SIFT还使用金字塔算法大大缩小了提取特征时的运算量。计算方法分为四个步骤：尺度空间极值提取、特征点定位、特征方向赋值和提取特征点描述。

（1）尺度空间极值检测

尺度空间理论是检测不变特征的基础。Witkin（1983）提出了尺度空间理论，他主要讨论了一维信号平滑处理的问题。Koenderink（1984）把这种理论扩展到二维图像，并证明高斯卷积核是实现尺度变换的唯一变换核。

一幅二维图像在不同尺度下的尺度空间表示可由图像与高斯核卷积得到：

L（x，y，σ）=G（x，y，σ）^*I（x，y） （4-12）

其中，G（x，y，σ）为高斯核函数。

其中，（x，y）为图像点的像素坐标，I（x，y）为图像数据。σ称为尺度空间因子，它是高斯正态分布的方差，反映了图像被平滑的程度，其值越小表征图像被平滑程度越小，相应尺度也越小。L（x，y，σ）代表了图像的尺度空间。

为高效地在尺度空间内检测出稳定的特征点，Lowe使用尺度空间中差分高斯（DifferenceofGaussian，DOG）极值作为判断依据。DOG算子定义为两个不同尺度的高斯核的差分，是归一化LoG（Laplacian-of-Gaussian，LOG）算子的近似。设k为两个相邻尺度间的比例因子，则DoG算子定义如下。

D（x，y，σ）=（G（x，y，kσ）-G（x，y，σ））^*I（x，y） （4-14）=L（x，y，kσ）-L（x，y，σ）

D（x，y，σ）构造方式如图4-18，其建立高斯图像（图中左列）与DoG（图中右列）两个金字塔。高斯图像金字塔分为多组，每组间又分为多层。一组中的多层间不同的是尺度，相邻层间尺度相差一个比例因子k。在S个尺度间隔内变化尺度因子，如使加倍，则k应为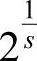。为了在整个金字塔内获取DoG极值，应在高斯金字塔中生σ成S+3层高斯平滑图像。下一组图像的最底层由上一组中尺度为2σ的图像进行因子为2的降采样得到，其中σ为上一组中最底层图像的尺度因子。DOG金字塔由相邻的高斯图像金字塔相减得到，如图4-19所示。

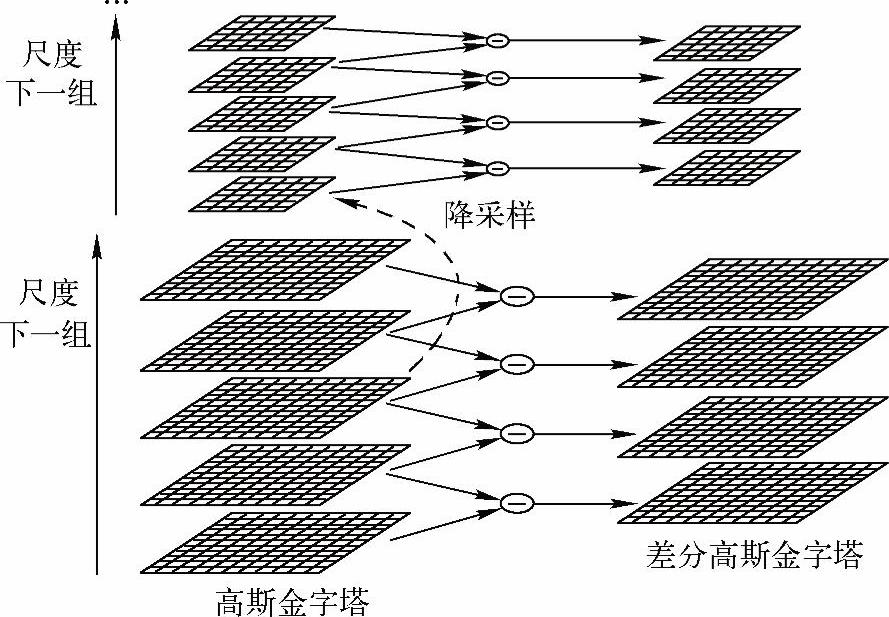
图4-18 高斯图像金字塔（S=2）与DOG金字塔

图4-19 所生成的高斯图像金字塔与DOG金字塔

金字塔中每个高斯图像的σ为：

其中，σ₀为基础尺度因子；o，s分别为图像所在的图像组坐标、组内层坐标，o∈o_min+[0，...，O-1]，s∈[0，...，S-1]；o_min是第一个金字塔组的坐标，通常o_min取0或者-1，当设为-1的时候，则图像在计算高斯尺度空间前先扩大一倍。在Lowe的算法实现中，以上参数的取值如下：，。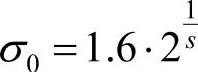

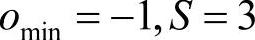此外，空间坐标x是组坐标o的函数。设x₀为第0组内的空间坐标，则有x=2^ox₀，x₀∈[0，...，N₀-1]×[0，...，M₀-1]，其中（N₀，M₀）是第0组中图像的分辨率。设（N₀，M₀）为第0

组中的图像分辨率，则其他组的分辨率为：

金字塔构造完后开始检测DoG局部极值。其中每个像素需要跟同一尺度的周围邻域8个像素和相邻尺度对应位置的周围邻域9×2个像素总共26个像素进行比较，如图4-20所示。仅当被检测点的DOG值大于此26个像素点或小于此26个像素点时才将该点判定为极值点并保存以进行后续计算。

（2）确定关键点位置及尺度

通过拟和三维二次函数以精确确定关键点的位置和尺度，得到原图像SIFT候选特征点集合，如图4-21所示。

在得到原图像的SIFT候选特征点集合X₀后，要从中筛选稳定的点作为该图像的SIFT特征点，其组成的集合用X表示。由于X₀中对比度较低的点对噪音较敏感，而位于边缘上的点难以准确定位，为确保SIFT特征点的稳定性，必须将这两种点剔除。(www.xing528.com)

1）剔除对比度低的点

将候选特征点x的偏移量定义为Δx，其对比度为D（x）的绝对值|D（x）|，对x的DOG函数表达式（4-14）进行泰勒级数展开

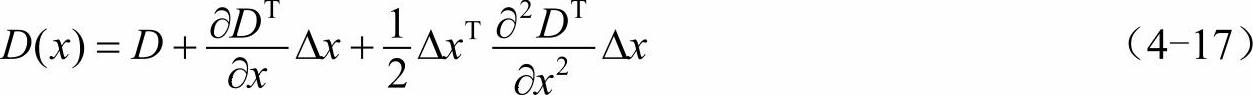
式中，由于x为DOG函数的极值点，所以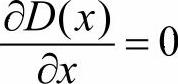，解方程得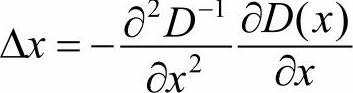，通过多次迭代得到最终候选点的精确位置及尺度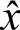，将其代入公式求得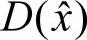，求其绝对值可得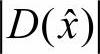。设对比度阈值为T_c，则低对比度点的剔除公式为

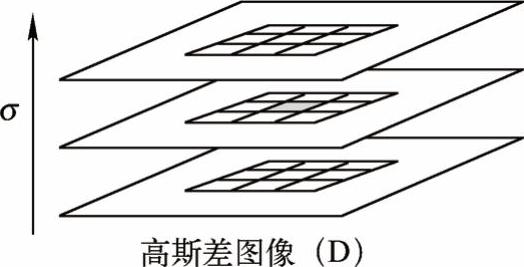
图4-20 DOG空间局部极值检测

图4-21 原图像的SIFT候选特征点集合

2）剔除边缘点

由于边缘梯度方向上主曲率值较大，而边缘方向上曲率较小，在边缘上得到的DOG函数的极值点与非边缘区域的点相比，其主曲率比值较大，因此可以将主曲率比值大于一定阈值的点视为位于边缘上的点将其剔除。

由于候选点的DOG函数D（x）的主曲率与2×2的Hessian矩阵H的特征值成正比。

式中，D_xx，D_xy，D_yy为候选点邻域对应位置的像素差分。令α为H的最大特征值，β为H的最小特征值，令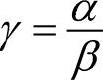，则D（x）的主曲率比值与γ成正比。由H的迹和行列式的值可得

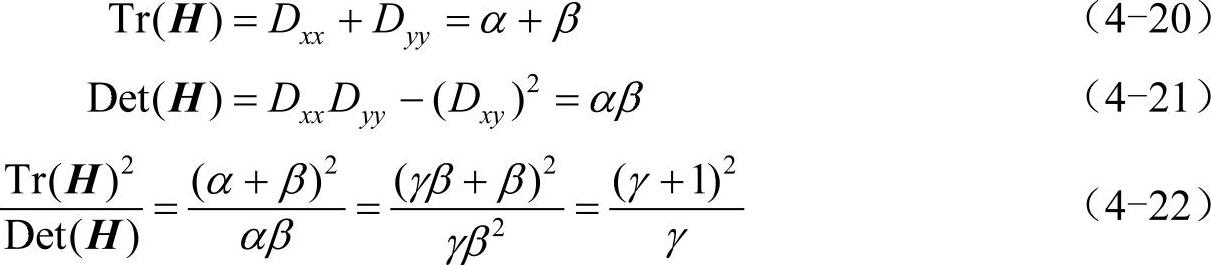
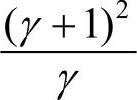只与两特征值之比有关，与特征值自身大小无关，当两特征值相等时最小，且随着γ的增大而增大。设主曲率比值阈值为T_γ，则边缘点的剔除公式为：

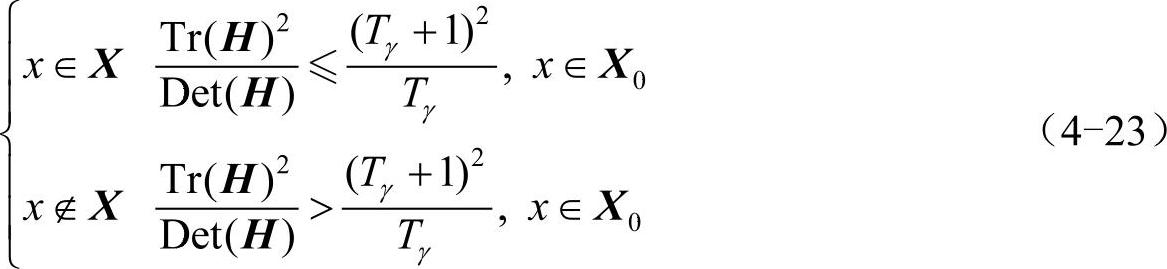
剔除低对比度和边缘点所剩的特征点如图4-22所示。

3）关键点方向确定

通过确定关键点的方向，可以使特征描述符以与方向相关的方式构造，从而使算子具有旋转不变性。关键点的方向利用其邻域像素的梯度分布特性确定。对每个高斯图像，每个点L（x，y）的梯度的模m（x，y）与方向θ（x，y）可以通过如下公式计算得到。

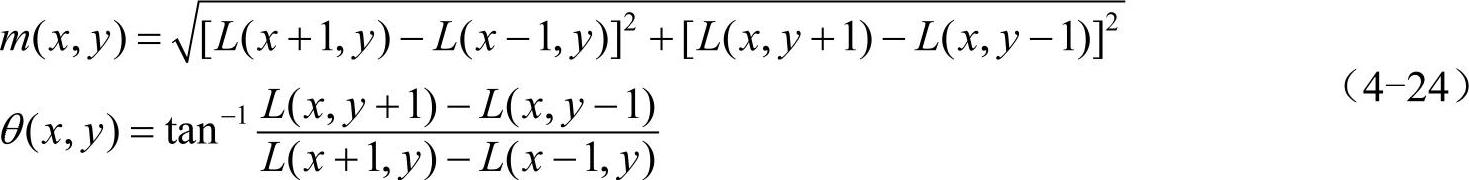
其中L（x，y）所用尺度为关键点所在尺度。

图4-22 剔除低对比度和边缘点后所剩的特征点