Harris角点检测的基本原理

人眼对角点的识别通常是在一个局部的小区域或小窗口完成的，如图4-9a所示。如果在各个方向上，移动这个特定的小窗口，窗口内区域的灰度发生了较大的变化，那么，就认为在窗口内遇到了角点，如图4-9b所示；如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点，如图4-9c所示；如果窗口在某一个（些）方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么，窗口内的图像可能就是一条直线的线段，如图4-9d所示。

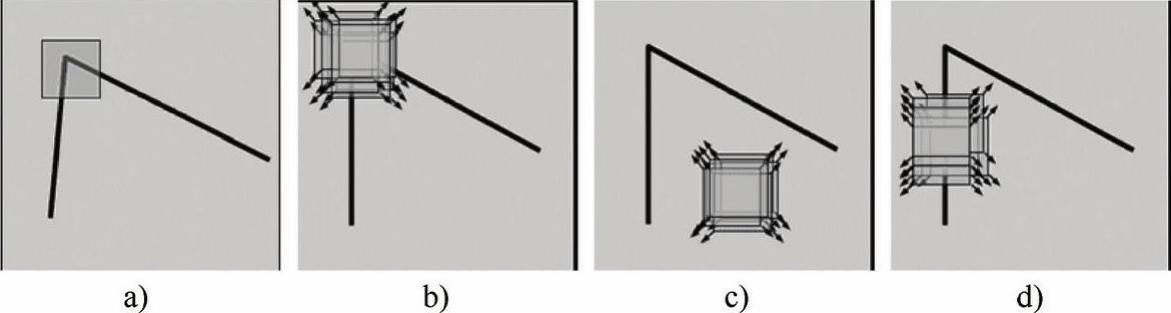
图4-9 窗口、窗口的移动与角点检测

对于图像I（x，y），当在点（x，y）处平移（Δx，Δy）后的自相似性可以通过自相关函数给出：

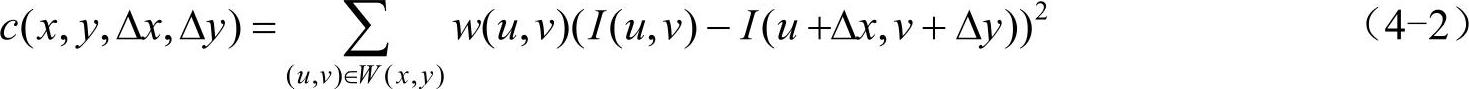
式中，W（x，y）是以点（x，y）为中心的窗口，w（u，v）为加权函数，它既可以是常数，又可以是高斯加权函数，如图4-10所示。

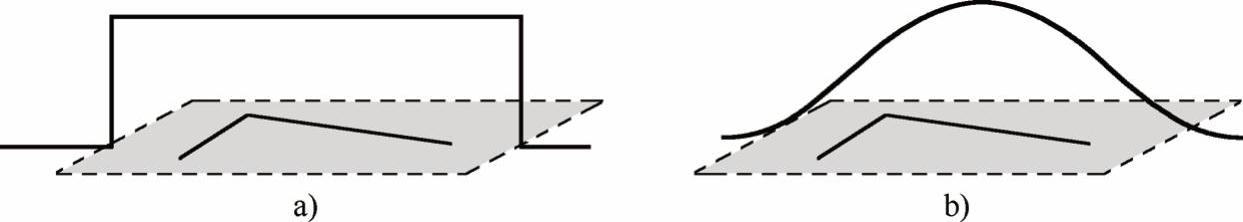
图4-10 加权函数

a）常数加权函数 b）高斯加权函数

根据泰勒展开，对图像I（x，y）在平移（Δx，Δy）后进行一阶近似：

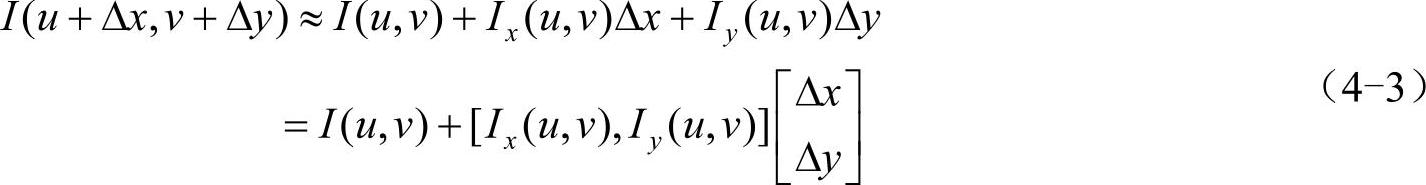
式中，I_x、I_y是图像I（x，y）的偏导数。这样，（4-2）可以近似为：

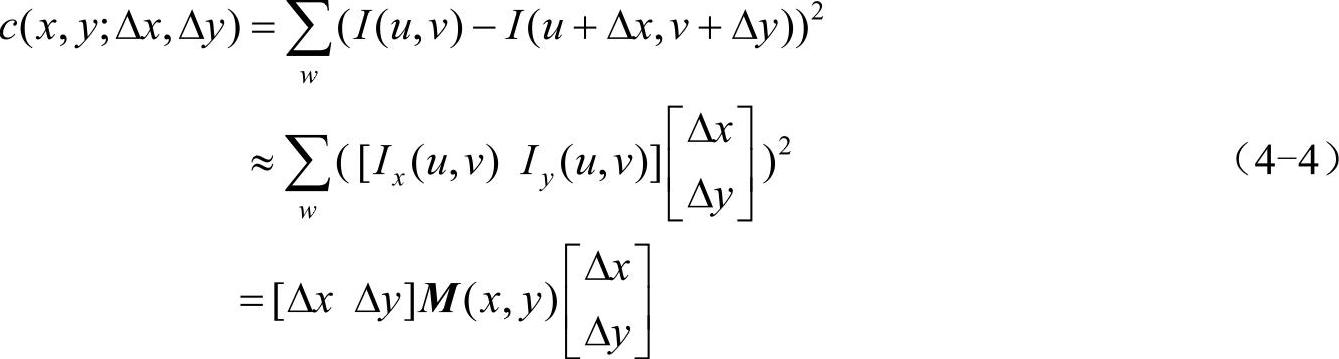
其中

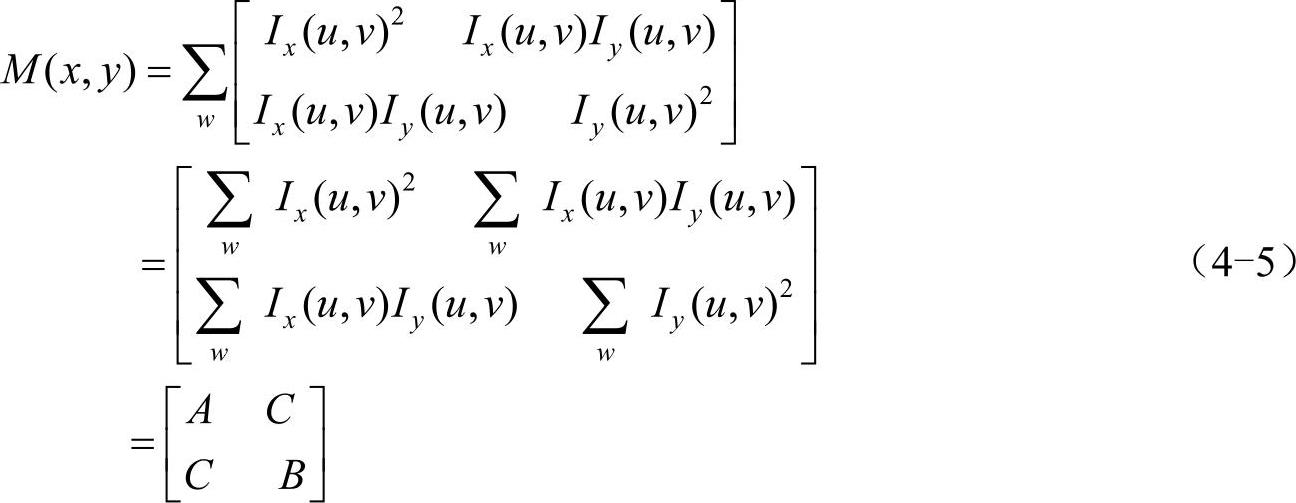
也就是说图像I（x，y）在点（x，y）处平移（Δx，Δy）后的自相关函数可以近似为二次项函数：(www.xing528.com)

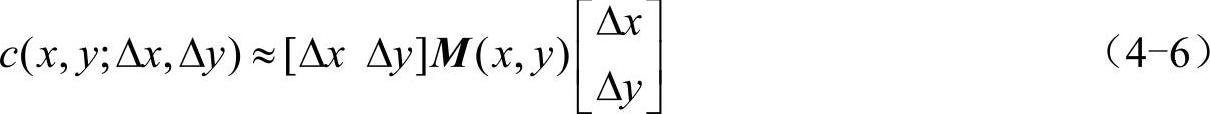
二次项函数本质上是一个椭圆函数，二次项特征值与椭圆变化的关系如图4-11所示。椭圆的扁率和尺寸是由M（x，y）的特征值λ₁、λ₂决定的，椭圆的方向是由M（x，y）的特征矢量决定的，椭圆的方程式为：

二次项函数的特征值与图像中的角点、直线（边缘）和平面之间的关系如图4-12所示。可分为三种情况：

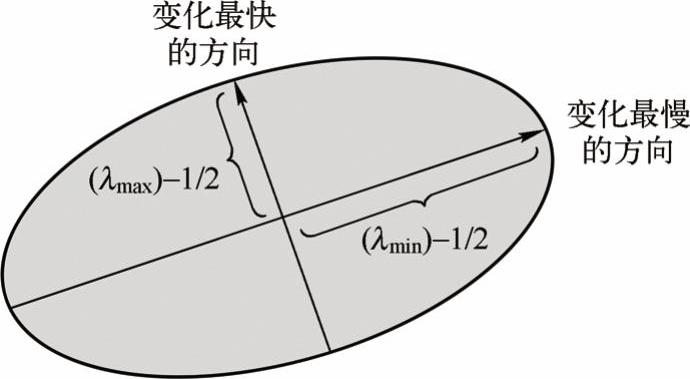
图4-11 二次项特征值与椭圆变化的关系

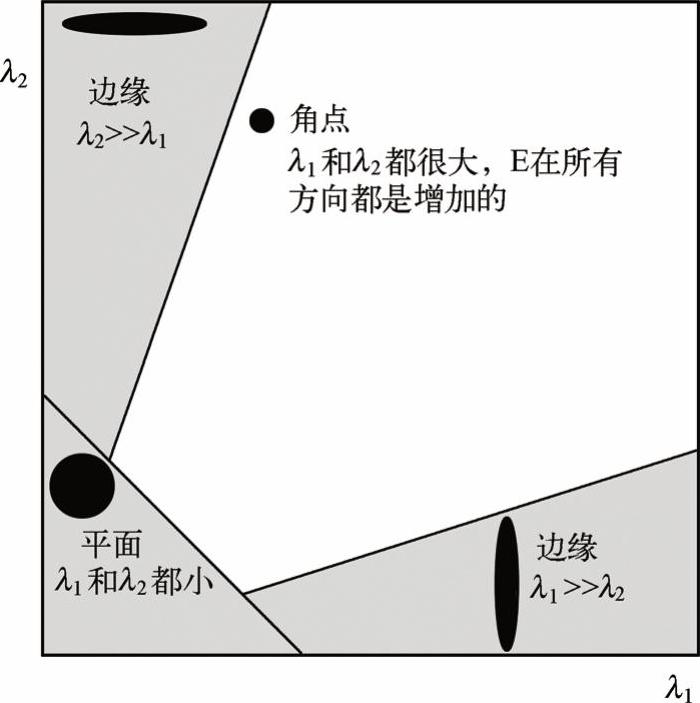
图4-12 特征值与图像中点线面之间的关系

➢图像中的直线。一个特征值大，另一个特征值小，即λ₁□λ₂或λ₁□λ₂。自相关函数值在某一方向上大，在其他方向上小。

➢图像中的平面。两个特征值都小，且近似相等；自相关函数值在各个方向上都小。

➢图像中的角点。两个特征值都大，且近似相等，自相关函数在所有方向上都增大。

根据二次项函数特征值的计算方法，可以求式（4-5）的特征值。但是Harris给出的角点判别方法并不需要计算具体的特征值，而是计算一个角点响应值R来判断角点。R的计算公式为

R=detM-α（traceM）2 （4-8）

式中，detM为矩阵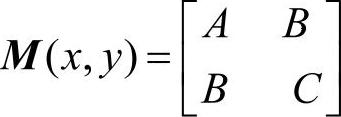的行列式；traceM为矩阵M的直迹；α为经验常数，取值范围0.04～0.06。实事上，特征值是隐含在detM和traceM中，因为：