基于SUSAN特征检测算子的边缘提取方法

SUSAN又称最小核值相似区，是Smallest Univalue Segment Assimilating Nucleus的缩写，是由牛津大学的Smith等人提出的。SUSAN使用一个原型模板和一个圆的中心点，通过圆中心点像元值与模板圆内其他像元值的比较，统计出与圆中心点像元值近似的像元数量，并与所设定的阈值进行比较，以确定是否是边缘。

定义一个半径为3.4个像元的圆，对于离散图像而言，这个圆共有37个像元。圆的中心像元称为模板的核（Nucleus），如图4-6所示，粗线包围的区域为离散圆。

在模板圆内，将与模板核像元值相似的像元数量或面积称为核值相似区（Univalue Segment Assimilating Nuceleus，USAN）面积，如图4-7所示，当模板圆在典型图像上移动时，在圆内，USAN面积是完全不同的。当圆形模板完全处在图像或背景中时，USAN区域面积最大；当模板移向图像边缘时，USAN区域逐渐变小；当模板中心处于边缘时，USAN区域很小；当模板中心处于角点时，USAN区域最小。可以看出，在边缘处像素的USAN值都小于或等于其最大值的1/2。因此，计算图像中每一个像素的USAN值，通过设定一个USAN阀值，查找小于阀值的像素点，即可确定为边缘点。

图4-6 SUSAN模板离散圆与核

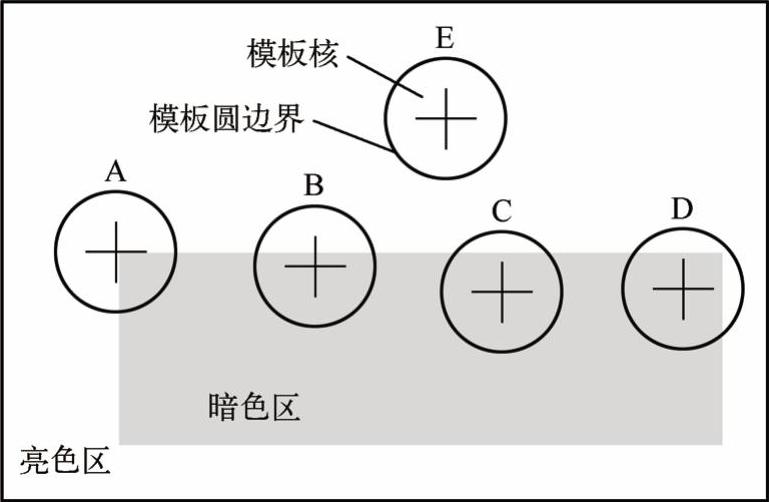
图4-7 模型和模板核在典型图像的不同位置的USAN变化

将圆形模板在被检测的图像上逐个像元移动，圆形模板内的像元值与核像元值进行比较。比较过程可用下式进行描述。

其中，r_o表示模板核在二维图像中的位置；r表示模板内其他任意位置；I（r_o）表示图像在r_o处的像元值；I（r）表示图像在r处的像元值；t为像元与其他像元相似度的阈值。当模板圆内的所有像元比较完成后，对结果c（r，r_o）进行累加，即

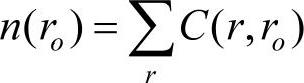
n（r_o）就是模板核在r_o处模板内图像USAN的像元数量，也即是模板核在r_o处图像USAN的面积。

得到每个像素的USAN值n（r_o）以后，再与预先设定得门限g进行比较，当n（r₀）＜g时，所检测到像素位置r_o可以认为是一个边缘点。

对于数字图像，实际上无法实现真正的圆形模板，所以都是采用近似圆代替。但当模板较小时，如果门限选取不恰当，可能会发生边缘点漏检的情况。模板也不宜取得太大，否则会增大运算量大，通常可取5×5或37像素模板。

门限g决定了边缘点的USAN区域的最大值，即只要图像中的像素的USAN值小于g，该点就被判定为边缘点。g过大时，边缘点附近的像素可能作为边缘被提取出来，过小则会漏检部分边缘点。g取0.75×n_max时（n_max为模板的最大USAN值）可以较好地提取出图像中的边缘点。

门限t表示所能检测边缘点的最小对比度，也是能忽略的噪声的最大容限。t越小，可从对比度越低的图像中提取特征。因此对于不同对比度和噪声情况的图像，应取不同的t值。

例程4-4的功能是实现运用SUNSAN算子进行边缘检测。

例程4-4

(www.xing528.com)

例程4-5所调用的子函数susan_threshold的MATLAB源代码如下所示。

例程4-5

例程4-4和例程4-5的运行结果如图4-8所示。

图4-8 例程4-4、4-5的运行结果

a）原始图像 b）采用SUSAN算子检测边缘的结果

基于SUSAN算子的边缘检测有如下优良性能。

（1）抗噪声能力好

由于USAN的求和相当于求积分，所以这种算法对噪声不敏感，而且SUSAN算法不涉及梯度的计算，所以该算法抗噪声的性能很好。很明显，如果考虑有独立同分布的高斯噪声，只要噪声小于USAN函数的相似灰度门限值，噪声就可被忽略。对局部突变的孤立噪声，即使噪声的灰度与核相似，只要局部USAN值小于门限g，也不会对边缘检测造成影响。因此SUSAN边缘检测算法可以用于被噪声污染的图像的边缘检测。

（2）算法使用灵活

由于基于SUSAN算法的边缘检测使用了控制参数t和g，因而，可以根据具体情况很容易地对不同对比度、不同形状的图像通过设置恰当的t和g来进行控制。例如，图像的对比度较大，则可选取较大的t值；而图像的对比度较小，则可选取较小的t值。所以这种算法非常适用于对某些低对比度图像或目标的识别。

（3）运算量小，速度快

对一幅256×256的图像，应用SUSAN算法进行计算，对每一点只需做8次加法运算，共需要做256×256×8次加法。而对于其他的经典的边缘检测算法，如果采用欧式距离作为梯度算子，Sobel算子采用两个3×3的模板，对每一点需要做9次加法，6次乘法，以及1次开方运算，则共需要做256×256×9次加法运算和256×256×6次乘法运算，以及256×256次开方运算。采用Gauss-Laplace算子、Priwitt算子以及Canny算子进行边缘检测的计算量就会更大。

（4）可以检测边缘的方向信息

SUSAN算法可以检测出边缘的方向信息。具体思想是：对每一个检测点计算模板内与该点灰度相似的像素集合的重心，检测点与该重心的连线的矢量垂直于这条边缘。

经验分享：傅里叶变换与梯度的关系

图像是由对在连续空间上的采样得到一系列点的集合，用户习惯用一个二维矩阵表示空间上各点，则图像可由z=f（x，y）来表示。由于空间是三维的，图像是二维的，因此，空间中物体在另一个维度上的关系就由梯度来表示，这样就可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度呢？因为实际上对图像进行二维傅里叶变换得到频谱图，就是图像梯度的分布图，当然频谱图上的各点与图像上各点并不存在一一对应的关系，即使在不移频的情况下也一样。在傅里叶频谱图上看到的明暗不一的亮点，实际上是图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。一般来讲，梯度大则该点的亮度强，否则该点亮度弱。这样通过观察傅里叶变换后的频谱图，也叫功率图。首先就可以看出图像的能量分布：如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小）；反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大。